Билет 1.

1.Тепловое излучение. Проблемы излучения абсолютно черного тела.

Тепловое излучение – это электромагнитное излучение, испускаемое веществом и возникающее за счет энергии теплового движения атомов и молекул (т.е. внутренней энергии).Тепловое излучение (ТИ) свойственно всем телам при температурах выше абсолютного нуля. ТИ можно поддерживать неизменным, подводя непрерывно к телу соответственное количество тепла. Т.е. тепловое излучение может быть равновесным, нетепловое – обязательно неравновесно. Если несколько нагретых (теплоизлучающих) тел окружить идеально отражающей, непроницаемой для излучения оболочкой, то по истечении некоторого интервала времени в системе «излучающие тела + излучение в полости» установится термодинамическое равновесие (рис.1). Следовательно, температуры тел выровняются, а распределение энергии между телами и излучением не будет меняться со временем. Такое равновесное состояние системы устойчиво, т.е. после всякого нарушения его, состояние равновесия восстанавливается.

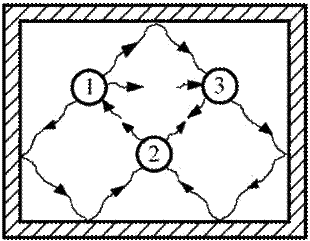
Рис. 1.

Причем, термодинамическое равновесие устанавливается в полости, стенки которой выполнены из любого реального материала и поддерживаются при некоторой неизменной температуре. Всякое другое излучение, возбуждаемое не нагреванием, а каким-либо иным способом, не приводит к установлению термодинамического равновесия. Например, если внутрь упомянутой выше полости поместить тело, светящееся благодаря предварительному облучению ультрафиолетовыми лучами, то свечение этого тела постепенно ослабнет и прекратится. Это произойдет потому, что поглощаемые телом лучи (находящиеся в полости благодаря отражению стенками оболочки) не способны вновь вызвать свечение тела. Таким образом, способность ТИ находиться в равновесии с излучающим телом отличает ТИ от других видов излучения тел, поскольку нетепловое излучение всегда неравновесно.

Проблема излучения абсолютно черного тела состояла в том, чтобы теоретически получить зависимость φ(λ,Т) - спектральную плотность энергетической светимости абсолютно черного тела.

Казалось, что ситуация ясна: при заданной температуре Т молекулы вещества излучающей полости имеют максвелловское распределение по скоростям и излучают электромагнитные волны в соответствии с законами классической электродинамики. Излучение находится в термодинамическом равновесии с веществом, значит для нахождения спектральной плотности энергии излучения u(λ,T) и связанной с ней функции φ(λ,Т) можно использовать законы термодинамики и классической статистики.

Однако, все попытки теоретиков получить на основе классической физики закон излучения абсолютно черного тела потерпели неудачу.

Частичный вклад в решение этой проблемы внесли Густав Кирхгоф, Вильгельм Вин, Иозеф Стефан, Людвиг Больцман, Джон Уильям Релей, Джеймс Хонвуд Джинс.

Проблема излучения абсолютно черного тела была решена Максом Планком. Для этого ему пришлось отказаться от классических представлений и сделать предположение о том, что заряд, совершающий колебания с частотой v, может получать или отдавать энергию порциями, или квантами.

Величина кванта энергии в соответствии с (1.2) и (1.4):

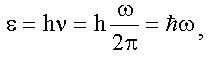
где h - постоянная Планка; v - частота колебаний электромагнитной волны, излученной колеблющемся зарядом; ω = 2πv - круговая частота.

На основе представления о квантах энергии М. Планк, используя методы статистической термодинамики, получил выражение для функции u(ω,Т), дающей распределение плотности энергии в спектре излучения абсолютного черного тела:

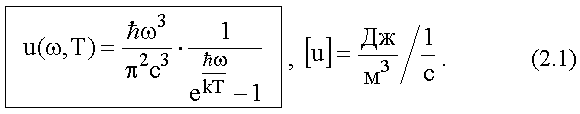
Вывод этой формулы будет дан в лекции N 12, § 3 после того, как мы познакомимся с основами квантовой статистики.

Для перехода к спектральной плотности энергетической светимости f(ω,Т) запишем вторую формулу (1.19):

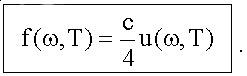
Используя это соотношение и формулу Планка (2.1) для u(ω,T), получим, что:

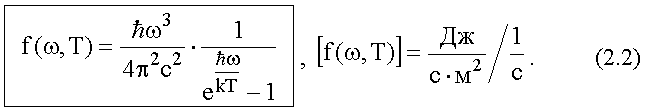
Это и есть формула Планка для спектральной плотности энергетической светимости f(ω,T).

Теперь мы получим формулу Планка для φ(λ,Т). Как мы знаем из (1.18), в случае абсолютно черного тела f(ω,T) = rω, а φ(λ,Т) = rλ.

Связь между rλ и rω дает формула (1.12), применяя ее мы получим:

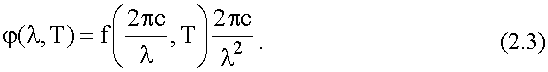
Здесь мы аргумент ω функции f(ω,Т) выразили через длину волны λ. Подставляя сюда формулу Планка для f(ω,Т) из (2.2), получим формулу Планка для φ(λ,Т) - спектральной плотности энергетической светимости в зависимости от длины волны λ:

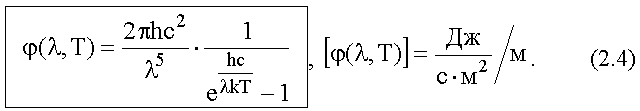
График этой функции хорошо совпадает с экспериментальными графиками φ(λ,Т) для всех длин волн и температур.

Это и означает, что проблем излучения абсолютно черного тела решена.