Самостоятельная работа № 4 по химии Раздел № 1. Обучающие задания с алгоритмами решения для закрепления темы «Теория растворов»

Пример 1. Расчеты концентрации растворов при различных способах

её выражения

1. В электрохимических аккумуляторах в качестве электролита применяется 34%-й раствор серной кислоты (плотность раствора ρ = 1,255 г/мл). Рассчитайте объемы воды и купоросного масла (концентрированной 94%-й 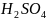, ρ = 1,840 г/мл), необходимые для приготовления 2 л такого электролита.

Решение. Сначала определим массу серной кислоты, содержащуюся в 2 л 34%-го раствора, используя формулу 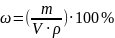. Преобразуем это выражение относительно m и рассчитаем массу серной кислоты:

; .

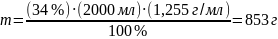Теперь определим, в каком объеме купоросного масла содержится 853 г , предварительно преобразовав формулу относительно объема :

; .

Ошибкой было бы предположить, что объем воды будет определяться как разность между объемом раствора (2 л) и объемом купоросного масла (493 мл). Хорошо известно, что серная кислота является сильным электролитом, взаимодействующим с растворителем, а потому объемы при смешении не суммируются. Для определения объема воды вычислим вначале массы раствора аккумуляторной кислоты и купоросного масла:

; ;

.

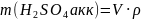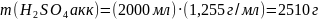Теперь вычислим массу воды, необходимую для приготовления раствора:

. Зная, что плотность химически чистой воды , определим объем воды:

; .

Ответ: .

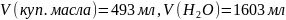2. К 0,8 л раствора натрия гидроксида ( ) прибавлено 0,4 л раствора этого же вещества, массовая доля в котором равна 14% ( ). Определите плотность полученного раствора и массовую долю в нём.

Решение. Первый способ. Для определения массовой доли и плотности раствора, полученного после смешивания, необходимо рассчитать его массу, а также массу растворенного вещества. Масса первого раствора будет равна:

.

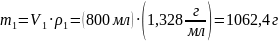В этом количестве раствора содержится гидроксида натрия:

.

Масса второго раствора равна:

.

В этом растворе содержится гидроксида натрия:

.

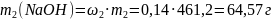Масса раствора после смешения

.

В этом растворе содержится растворённого вещества:

.

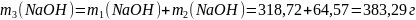Теперь легко определить массовую долю в полученном растворе:

.

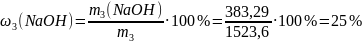Плотность раствора рассчитывается как частное от деления его массы на объем, равный условно :

.

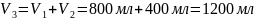Второй способ. Задачи такого типа (на смешивание растворов с разной массовой долей растворенного вещества) легко решаются с помощью диагональной схемы или «правила креста»: слева одно под другим записывают значения исходных концентраций смешиваемых растворов. От них проводят диагональные отрезки и в точке их пересечения записывают значение концентрации раствора, получаемого после смешивания, а у других концов отрезков – разности между значениями концентраций смеси и её компонентов, учитывая то, что эти величины должны оставаться положительными (т.е. от большего значения необходимо отнимать меньшее). Неизвестные значения при этом обозначаем буквой «x».

Диагональная схема на примере данной задачи выглядит так:

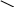
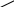
30. x -14

x

14 30 - x

Схема читается следующим образом: массы смешиваемых растворов и обратно пропорциональны разностям концентраций смеси и компонентов, т.е.

.

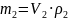Решим эту пропорцию относительно x, помня, что и , т.е.

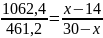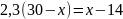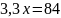; ; ; . Мы получили значение концентрации раствора после смешивания – .

Плотность раствора, как и в предыдущем способе, определяется по формуле:

; .

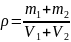Ответ: массовая доля полученного раствора 25 %, его плотность 1,27 г/мл.

3. Определите массу кристаллогидрата K₂CO₃·5H₂O, необходимого для приготовления 0,25 л 0,03 н. раствора. Рассчитайте молярность этого раствора.

Решение. Молярная концентрация эквивалента раствора прямо пропорциональна количеству вещества эквивалентов: 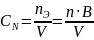(моль/л), где B – суммарная валентность ионов металла соли. Преобразуем это выражение относительно количества растворенного вещества n и произведем расчеты:

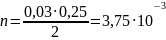; моль.

Масса кристаллогидрата определяется по формуле 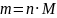, где М – молярная масса K₂CO₃·5H₂O (М = 2·39 + 12 + 3·16 + 5·18 = 228 г/моль):

m = 228(г/моль)·3,75·10^-3(моль) = 0,855 г.

Для определения молярности раствора используем формулу: , следовательно,

.

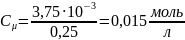Ответ: m(K₂CO₃·5H₂O) = 0,855 г, С_μ = 0,015 моль/л.

4. Вычислите массовую долю, молярность, моляльность, молярную концентрацию эквивалента, молярную долю и титр раствора свинца (2) нитрата, если к 100 мл его 30 %-го раствора добавили 200 мл воды и получили раствор с плотностью 1,109 г/мл.

Решение. Сначала определим массовую долю растворенного вещества после разбавления раствора водой, используя «правило креста»:

30 x

x

0 30 - x.

Отсюда 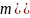, далее .

Для решения полученного уравнения относительно x вспомним, что плотность жидкой воды в широком интервале температур постоянна и равна , а по справочной таблице найдем плотность 30 %-го раствора свинца (2) нитрата : ρ₁ = 1,328 г/мл. Подставим эти значения в полученное уравнение и решим его:

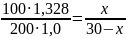; 0,664(30-x) = x; x = 11,97 ≈ 12.

Таким образом, после разбавления массовая доля раствора свинца нитрата ω₂ = 12 %.

Масса растворенного вещества в разбавленном растворе осталась такой же, как и в исходном растворе Pb(NO₃)₂, тогда m(Pb(NO₃)₂) = ω₁·V₁·ρ₁ = 0,30·100·1,328 = 39,84 г.

Зная по условию задачи плотность второго раствора, полученного после разбавления, определим его объем:

; .

Рассчитанной нами массе соли соответствует количество вещества:

; .

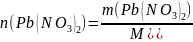Теперь легко определить молярность и нормальность (молярную концентрацию эквивалента) раствора:

; С_N = С_μ·B = 0,4·2 = 0,8 .

Для определения моляльности необходимо предварительно рассчитать :

;

.

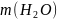Рассчитаем моляльность раствора:

; .

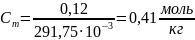Для определения молярной доли растворенной соли χ(Pb(NO₃)₂) по формуле

необходимо предварительно рассчитать количество вещества воды:

; и тогда ;

или .

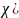И, наконец, титр раствора рассчитываем по формуле: ,

.

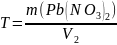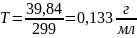Ответ: ω = 12%; С_μ = 0,4 моль/л; С_N = 0,8 моль/л; С_m = 0,41 моль/кг; χ = 0,7%; Т = 0,133 г/мл.

5. Для осаждения в виде BaSO₄ всего бария, содержащегося в 100 мл раствора бария хлорида, потребовалось 50 мл 0,1 н. раствора серной кислоты. Определите молярную концентрацию раствора бария хлорида и массу выпавшего в осадок бария сульфата.

Решение. В любой химической реакции вещества взаимодействуют между собой в количествах, пропорциональных их эквивалентам. Значит, для реакции

BaCl₂ + H₂SO₄ = BaSO₄↓ + HCl

справедливо равенство n_Э(BaCl₂) = n_Э(H₂SO₄) = n_Э(BaSO₄). А поскольку n_Э = С_N·V, то можно записать и закон эквивалентов для взаимодействующих растворов:

С_N(BaCl₂)·V(BaCl₂) = C_N(H₂SO₄)·V(H₂SO₄).

Преобразуем это уравнение относительно неизвестной молярной концентрации эквивалента бария хлорида и решим его:

; .

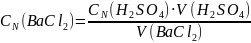Молярная и нормальная концентрации связаны соотношением С_N = С_μ·B, откуда 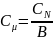и значит, .

Количество вещества бария сульфата в осадке равно количеству вещества бария хлорида, вступившего в реакцию, следовательно, в осадок выпало

n(BaSO₄) = n(BaCl₂) = С_μ(BaCl₂)·V(BaCl₂) = 0,025·0,01 = 2,5·10^-4 (моль).

Теперь легко рассчитать массу осадка, зная, что молярная масса бария сульфата M(BaSO₄) = 137 + 32 + 4·16 = 233 г/моль:

m(BaSO₄) = n(BaSO₄)·M(BaSO₄) = 2,5·10^-4·233 = 0,058 г.

Ответ: С_N(BaCl₂) = 0,05 моль/л; С_μ(BaCl₂) = 0,025 моль/л; m(BaSO₄) = 0,058 г.