2. Теорема Максвелла.

Рассмотрим два состояния системы. В первом состоянии к систе­ме приложена сила P₁=1, а во втором — сила P₂=1 (рис. 5.12).

Обозначим перемещения, вызванные единичными силами или моментами (т. е. силами Р=1 или моментами М=1), знаком δ в отличие от перемещений, вызванных силами и моментами, не рав­ными единице, обозначаемых знаком ∆. В соответствии с этим пере­мещение рассматриваемой системы по направлению единичной силы. P₂ в первом состоянии (т. е. вызванное силой P₁=1) обозначим δ₂₁. а перемещение по направлению единичной силы P₁ во втором состоянии обозначим δ₁₂ (рис. 5.12).

На основании теоремы о взаимности работ для рассматриваемых двух состояний

но так как

То или в общем случае действия любых единичных сил  (5.21)

Полученное равенство носит название теоремы о взаимности перемещений (теоремы, или принципа, Максвелла): для двух единичных состояний упругой системы перемещение по направлению первой единичной силы, вызванное второй единичной силой, равно перемещению по направлению второй силы, вызванному первой силой. Для иллюстрации теоремы Максвелла в качестве примера рас смотрим два состояния балки, изображенной на рис. 5.13.

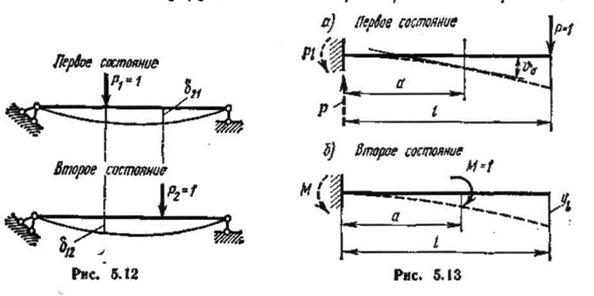
В первом состоянии на балку действует сила Р=1, а во втором — момент Угол поворота ϑ_a, вызванный силой Р=1, на основании формулы (5.21) должен быть численно равен прогибу y_l вызванному моментом M=1, т. е. ϑ_a=y_l

Определим значения ϑ_a и y_l методом начальных параметров. В первом состоянии (рис. 5.13, а)

во втором состоянии (рис. 5.13,б)

При M=P=1

Т.е

Единичные перемещения (например, перемещения, вызванные отвлеченной единичной силой Р=1 или отвлеченным единичным моментом М=1) имеют размерности, отличные от обычных размер­ностей перемещений. Размерность единичного перемещения представ­ляет собой размерность отношения перемещения (не единичного) к вызвавшей его нагрузке. Так, например, в рассмотренном при­мере единичный угол поворота ϑa, вызванный силой P=1, выражен в 1/кН, единичный прогиб yl, вызванный моментом M=1, выражен в м/кН*м, или 1/кН, т. е. в тех же функциях, что и угол ϑa.

Билет №14.

1. Определение осевых перемещений при растяжении и сжатии.

Осевое или центральное растяжение (сжатие) относят к простым видам сопротивления. Название этого вида деформации обусловлено тем, что линия действия сил (равнодействующей сил), приложенных к стержню, совпадает с осью стержня (ось стержня проходит через центры тяжести поперечных сечений).

Продольное внутреннее усилие (N) будет положительным при растяжении элемента и отрицательным в случае сжатия.

Продольное внутреннее усилие (N) в любом сечении равно алгебраической сумме проекций всех внешних сил (включая опорные реакции), взятых по одну сторону от сечения, на продольную ось стержня.

Напряжения в поперечных сечениях характеризуют интенсивность внутренних сил в поперечном сечении

Соотношение (6.1) позволяет вычислить среднее напряжение по площади поперечного сечения. Бернулли были предложены допущения – гипотезы плоских сечений: поперечные сечения, плоские до нагружения остаются плоскими и перпендикулярными продольной оси и после нагружения. В силу принятых гипотез σ_y=σ_z=τ_yx=τ_yz=0, σ_x≠0, поэтому напряженное состояние в элементе объёма – линейное (только одно из главных напряжений отлично от нуля), рис. 6.1. Нормальное напряжение в поперечном сечении при данном виде деформации является функцией от продольного внутреннего усилия N_x и зависит от геометрической характеристики поперечного сечения – площади А. Определяют напряжение по формуле σ=σ_x=N_x/A. (6.2)

Знак у напряжения определяется знаком продольной силы.

При растяжении (сжатии) различают абсолютные ∆l и относительные ε деформации. Абсолютная деформация – это разница между длиной стержня до и после деформации, т.е. та величина, на которую он изменил свою длину ∆l=/l₁-l/. Относительная деформация – это, как ясно из названия, отношение абсолютной деформации к первоначальной длине стержня ε=∆l/l.

Деформации элементов конструкций, материал которых работает в упругой стадии, определяются на основании закона Гука, записанного в случае одноосного(линейного) напряжённого состояния в следующем виде:  (6.3)

Закон Гука (6.3) устанавливает прямопропорциональную зависимость между действующим в рассматриваемой точке нормальным напряжением  и относительной линейной деформацией материала  (по направлению  ). Коэффициент пропорциональности Е носит название модуля упругости первого рода (модуля продольной упругости, модуля Юнга) и имеет размерность напряжения.

В результате растяжения (сжатия) сечения стержня перемещаются. Осевое перемещение одного сечения относительно другого равно изменению длины участка стержня между этими сечениями. График, показывающий перемещения всех сечений стержня относительно неподвижного (или условно принятого за неподвижное), называют эпюрой перемещений.

Перемещения сечений происходят в результате деформирования стержня. Перемещения, соответствующие удлинению считаются положительными. Перемещения, вызванные внешними силовыми факторами, определяют с помощью зависимости (6.5).

В случае, когда в пределах грузового участка внутреннее усилие и жёсткость стержня постоянны, это выражение принимает вид

Перемещения, вызванные изменением температуры, определяются с помощью зависимости