2. Формула Мора для определения перемещений.

Интеграл Мора позволяет определять прогибы и углы поворота заданного сечения балки, используя интегральное исчисление. Хотя данный метод предпочтительнее метода начальных параметров, он неудобен из-за необходимости вычисления интеграла. Из интеграла Мора был получен удобное для практического применения правило Верещагина, при котором не нужно вычислять интегралы, а только нужно находить площадь и центр тяжести эпюр.

Получение формулы интеграла Мора

Рассмотрим балку.

Обозначим и , соответственно, изгибающий момент и поперечную силу, возникающие в заданной балке от действующей на нее группы нагрузок P. Пусть требуется определить прогиб балки ( ) в точке K.

Введем в рассмотрение вспомогательную балку (та же балка, но нагруженная только единичной силой либо единичным изгибающим моментом). Нагрузим ее только одной силой (рис. б). Единичную силу приложим в точке K, где нужно определить прогиб.

Внутренние усилия, возникающие во вспомогательной балке, обозначим и .

Воспользуемся теперь теоремой о взаимности работ, согласно которой работа внешних сил, приложенных к вспомогательной балке на соответствующих перемещениях заданной балки равна взятой с обратным знаком работе внутренних сил заданной балки на соответствующих перемещениях вспомогательной балки. Тогда .

При определении перемещений в балке, как правило, можно пренебрегать влиянием поперечной силы, ( не учитывать второе слагаемое).

Тогда, учитывая, что , окончательно получим формулу интеграла Мора: .

Определение перемещений по формуле интеграла Мора часто называют определением перемещений методом Мора, а саму формулу – интегралом Мора.

Входящие в интеграл Мора изгибающие моменты берутся в произвольном поперечном сечении и поэтому представляют собой аналитические функции от текущей координаты z.

Заметим, что если мы хотим в этой же точке K определить угол поворота поперечного сечения ( ), то нам необходимо к вспомогательной балке приложить не единичную силу, а единичный момент (рис. в).

билет №13.

1. Напряжения в наклонных сечениях при растяжении и сжатии.

При растяжении бруса наклонные сечения, как и поперечные, остаются плоскими и параллельными. Следовательно, внутренние силы распределены по наклонным сечениям равномерно.

При растяжении:

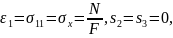
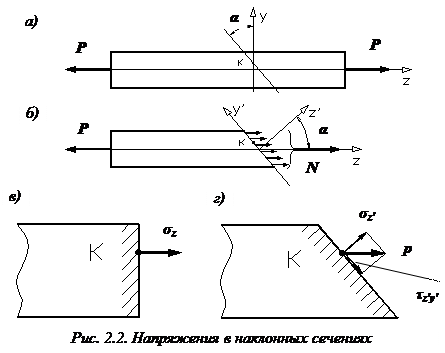
При сжатии: .

Напряжения в наклонных площадках наблюдаются, если мысленно «разрезать» стержень, растягиваемый силами P, наклонной плоскостью под углом 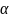 к поперечному сечению (рис. 2.2, а), проходящей через точку K, и отбросить правую часть.

Внешняя нормаль  к наклонному сечению будет составлять с осью  угол . Действие отброшенной правой части стержня на левую часть заменим внутренними усилиями (рис. 2.2, б). Чтобы левая часть стержня находилась в равновесии, в каждой точке наклонного сечения стержня должно возникнуть продольное противодействующее усилие. Равнодействующая внутренних усилий N равна внешней силе P.

Допустим, внутренние усилия равномерно распределены по площади наклонного сечения 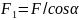 . Тогда полное напряжение наклонного сечения в каждой точке будет равно:

где 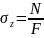 – нормальное напряжение, возникающее в точках (в том числе и в точке К), но в поперечном сечении стержня (рис. 2.1, в).

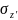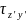Разложим полное напряжение в наклонном сечении (p), возникающее в некоторой точке К, на две составляющие – нормальное ( ) и касательное ( ) напряжения (рис. 2.2, г). Они будут равны:

; .

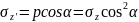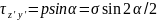Проследим, как будет меняться каждое из этих напряжений с изменением угла наклона сечения, проходящего через точку К, от нуля до 90̊.

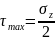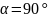При увеличении угла  нормальное напряжение в точке К будет постепенно уменьшаться от своего максимального значения ( ) до нуля. Касательное напряжение при этом будет сначала возрастать от нулевого до максимального значения ( ) при  , а затем убывать и при угле  снова станет равным нулю.

Следовательно, наибольшее нормальное напряжение действительно возникает в точках поперечного сечения стержня. В продольном сечении оно равно нулю. Следовательно, продольные волокна не давят друг на друга.

Наибольшие касательные напряжения возникают в наклонных сечениях, расположенных под углом 45̊ к оси стержня. В поперечном и продольном сечениях они равны нулю.