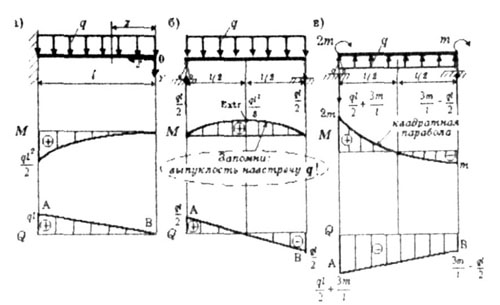
- •2.Внутренние усилия при изгибе.Их дифференциальная зависимость.
- •1) Изменение моментов инерции при повороте координатных осей
- •2)Нормальные и касательные напряжения при поперечном изгибе.
- •1) Главные моменты Инерции
- •2) Расчет балок на прочность при изгибе
- •1. Осевой момент инерции круга.
- •2. Метод начальных параметров.
- •1. Осевой момент инерции кольца.
- •2. Формула Мора для определения перемещений.
- •1. Напряжения в наклонных сечениях при растяжении и сжатии.
- •2. Теорема Максвелла.
- •Определение осевых перемещений при растяжении и сжатии.
- •Моменты инерции треугольника.
- •1. Статически неопределимые задачи при растяжении и сжатии.
- •2. Закон Гука при кручении.
- •1. Диаграммы растяжения и сжатия. Механические свойства материалов.
- •2. Закон Гука при изгибе.
Билет1 СТАТИЧЕСКИЕ МОМЕНТЫ СЕЧЕНИЯ |
|
|
При определении положения центра тяжести сечения необходимо определять значения статических моментов этого сечения. |
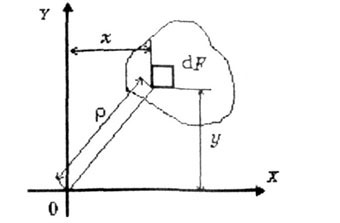
Статическими
моментами ппощади сечения относительно
осей X и У (рис.4.3) называются определенные
интегралы вида
|
|
|
|
где F - площадь сечения; X и у - координаты элемента площади dF. |
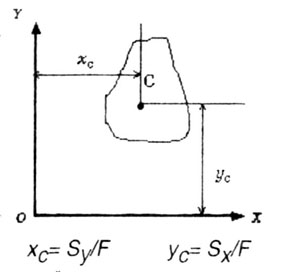
Если известно положение центра тяжести сечения (рис. 4.4). то статические моменты сечения могут быть подсчитаны по простым формулам, без взятия интегралов, а именно |
|
где Xc и Yc - координаты центра тяжести сечения. |
Из выражений (2) можно определить координаты центра тяжести сечения Xc и Yc: |
С |
|
Оси, проходящие через центр тяжести сечения -называются центральными. Центр тяжести сечения лежит на оси симметрии сечения. Если сечение имеет хотя бы две оси симметрии, то центр тяжести лежит на пересечении этих осей. |
Для сложного сечения, состоящего из n простейших фигур, координаты центра тяжести сечения определяются по формулам |
|
где Xj и Yj - координаты центров тяжести отдельных фигур сечения.
ОПРЕДЕЛЕНИЕ УГЛОВ ЗАКРУЧИВАНИЯ СТЕРЖНЕЙ КРУГЛОГО СЕЧЕНИЯ Кручение – простой вид сопротивления (нагружения), при котором на стержень действуют моменты в плоскостях, перпендикулярных к продольной оси стержня.
Стержень, работающий на кручение, в дальнейшем будем называть валом .
|
Р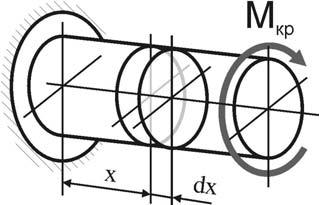 ассмотрим
деформацию элемента стержня (вала)
длиной dx,
выделенного из закручиваемого стержня
в произвольной точке с координатой x.
ассмотрим
деформацию элемента стержня (вала)
длиной dx,
выделенного из закручиваемого стержня
в произвольной точке с координатой x.
Условно примем, что левое сечение элемента dx остается неподвижным, а правое поворачивается на угол dϕ, создаваемый за счет закручивания вала на
длине dx. Один из радиусов OB, оставаясь прямым, поворачивается вместе с сечением на угол dϕ, при этом точка B переходит в положение B1, а образующая CB – в положение CB1, поворачиваясь на угол γ – угол сдвига в этой точке вала.
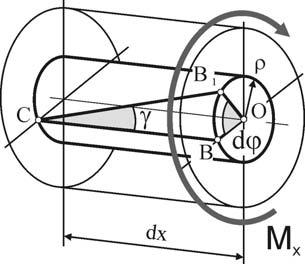
Длину дуги BB1 найдем из рассмотрения треугольников OBB1 и CBB1:
∪ BB1 =ρ*dϕ=γ*dx ⇒
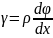
Полный момент во всем сечении:
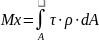
Закон Гука, связывающий касательные напряжения с углом сдвига
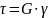
Подставляем сюда формулу угла сдвига, получится
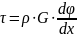
А это – в формулу полного момента в сечении, получится:
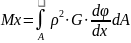
Bеличины G и dϕ/dx, в соответствии с принятыми гипотезами, остаются постоянными по данному сечению, то их можно вынести за знак интеграла:
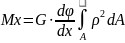
Величина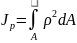 называется
полярным моментом инерции и является
геометрической характеристикой данного
сечения.
Таким
образом, окончательно можем записать
называется
полярным моментом инерции и является
геометрической характеристикой данного
сечения.
Таким
образом, окончательно можем записать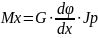
Величина
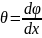 называется относительным
(погонным)
углом
закручивания
и имеет размерность рад/м.
называется относительным
(погонным)
углом
закручивания
и имеет размерность рад/м.
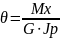
Зная эти формулы для определения относительного угла закручивания, можно записать формулу для определения взаимного угла поворота двух сечений, расположенных на расстоянии l друг от друга:

Если в пределах участка длиной l крутящий момент и геометрические характеристики сечения вала остаются постоянными, то угол закручивания можно определить как
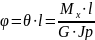
Билет2
ОСЕВЫЕ МОМЕНТЫ ИНЕРЦИИ
Осевой момент инерции фигуры - это интеграл произведений элементарных площадей на квадраты их расстояний до рассматриваемой оси. Формулы осевого момента инерции произвольной фигуры (см. рис. 4.1) относительно осей x и y:
![]()
Полярный момент инерции фигуры относительно данной точки (полюса) - это интеграл произведений элементарных площадей на квадраты их расстояний до полюса:
![]()
Если
через полюс проведена система взаимно
перпендикулярных осей x и y, то ![]() ,
и формула
полярного момента инерции равна
сумме осевых моментов инерции относительно
осей x и y:
,
и формула
полярного момента инерции равна
сумме осевых моментов инерции относительно
осей x и y:
![]()
Из
формул осевых
и
полярного
моментов
инерции видно: значения осевых и полярного
моментов инерции всегда положительны,
так как координаты
![]() и
расстояние
и
расстояние ![]() возведены
в квадрат.
возведены
в квадрат.
РАСЧЕТЫ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ ПРИ КРУЧЕНИИ
При расчетах на прочность при кручении (также как и при растяжении) могут решаться три задачи:
а) проверочный расчет – проверить выдержит ли вал приложенную нагрузку; б) проектировочный расчет – определить размеры вала из условия его прочности; в) расчет по несущей способности – определить максимально допустимый крутящий момент.
При проверочном расчете на прочность рекомендуется следующий порядок расчета валов при кручении:
по схеме вала и действующим на него скручивающим моментам строят эпюру внутренних крутящих моментов по отдельным участкам;
выбирают материал для рассчитываемого вала и определяют для этого материала допускаемое напряжение [τ]=[σ]/2; 3) для участка вала с максимальным по модулю значением крутящего момента записывают условие прочности при кручении
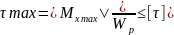
Проектировочный расчет проводится, исходя из условия прочности на основе следующего соотношения:
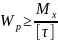
Для
сплошного круглого сечения Wρ
=π*d3
![]() 16
, отсюда можем записать выражение для
определения диаметра вала из условия
его прочности:
16
, отсюда можем записать выражение для
определения диаметра вала из условия
его прочности:
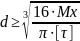
Определив размеры вала из условия прочности, проверяют вал на жесткость по формуле
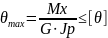
здесь [θ] – допустимый относительный угол закручивания вала.
Если данное условие не выполняется, то необходимо выбрать размеры вала из условия жесткости:
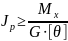
Учитывая, что для сплошного круглого сечения Jρ =π*d 4 32 , можем записать выражение для определения диаметра вала из условия его жесткости:
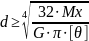
Окончательно выбирают диаметр d, удовлетворяющий условиям прочности и жесткости.
Билет 3
1.Центробежным моментом инерции сечения относительно осей x и y называется сумма произведений элементарных площадок dA на их расстояния до этих осей:
Jxy=![]() AxydA
где
x,у — расстояние от элементарной площадки
dA до осей х и y (смотри рисунок).
AxydA
где
x,у — расстояние от элементарной площадки
dA до осей х и y (смотри рисунок).
Центробежный момент инерции может быть положительным, отрицательным и, в частном случае, равным нулю. Если взаимно перпендикулярные оси x и y или одна из них являются осями симметрии фигуры, то относительно таких осей центробежный момент инерции равен нулю. Jxy=0.
П J |
|
2.Статически
неопределимые задачи.
При
кручении, так же как и при растяжении,
встречаются задачи, которые не могут
быть решены с помощью одних только
уравнений равновесия. В таких задачах
количество неизвестных превышает число
уранений равновесия. Порядок решения
таких задач тот же самый, что и при
решении статически неопределимых задач
при растяжении (сжатии).
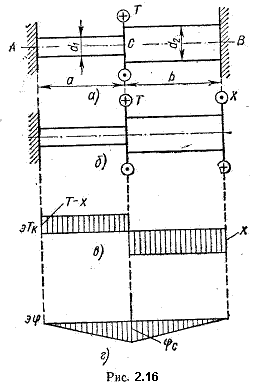
Рассмотрим для примера стержень с двумя заделанными концами (рис. 2.16, а). Такой стержень статически неопределим, так как для нахождения двух реактивных моментов, возникающих в заделках, статика дает лишь одно уравнение равновесия.
Отбросим
одну заделку, заменив ее действие
неизвестным моментом Х (рис. 2.15, б).
Дополнительное уравнение (называемое,
как известно, уранением деформации или
уравнением перемещений) получим из
условия, что угол поворота сечения у
отброшенной заделки, равный углу
закручивания стержня под действием
моментов Т и Х, равен нулю (![]() =
0).
=
0).
В
получившейся статически определимой
системе, называемой основной системой,
поворот сечения В происходит под
действием внешнего момента и момента
Х. Угол поворот сечения В под действием
момента Х равен
![]() где
где ![]()
Угол
поворота сечения В под действием момента
Т равен
![]() Подставляя
эти значения и уравнение перемещений,
получаем
Подставляя
эти значения и уравнение перемещений,
получаем
![]() Отсюда
определяем Х.
Отсюда
определяем Х.
После
этого можно определить крутящий момент
в любом сечении и построить эпюру Тк и
эпюру углов закручивания. Для построения
эпюры ![]() достаточно
вычислить угол поворота сечения С. Он
равен
достаточно
вычислить угол поворота сечения С. Он
равен
![]()
Углы поворота сечений А и В равны нулю, а так как угол поворота сечения линейно зависит от расстояния [см. формулу (2.19)], то полученные точки эпюры можно соединить прямыми линиями. Эпюры Тк и представлены на рис. 2.16, в, г
Билет 4
1.Моменты инерции относительно параллельных осей.
Задачу — получить наиболее простые формулы для вычисления момента инерции любой фигуры относительно любой оси — будем решать в несколько приемов. Если взять серию осей, параллельных друг другу, то оказывается, что можно легко вычислить моменты инерции фигуры относительно любой из этих осей, зная ее момент инерции относительно оси, проходящей через центр тяжести фигуры параллельно выбранным осям.
 Рис.1. Расчетная
модель определения моментов инерции
для параллельных осей.
Рис.1. Расчетная
модель определения моментов инерции
для параллельных осей.
Оси,
проходящие через центр тяжести, мы будем
называть центральными
осями.
Возьмем (Рис.1) произвольную фигуру.
Проведем центральную ось Оу,
момент инерции относительно этой оси
назовем ![]() .
Проведем в плоскости фигуры
ось
.
Проведем в плоскости фигуры
ось![]() параллельно оси у на
расстоянии
параллельно оси у на
расстоянии ![]() от
нее. Найдем зависимость между
от
нее. Найдем зависимость между ![]() и
и ![]() —
моментом инерции относительно оси
.
Для этого напишем выражения для
и
.
Разобьем площадь фигуры на площадки
—
моментом инерции относительно оси
.
Для этого напишем выражения для
и
.
Разобьем площадь фигуры на площадки ![]() ;
расстояния каждой такой площадки до
осей у и
назовем
;
расстояния каждой такой площадки до
осей у и
назовем ![]() и
и ![]() .
Тогда
.
Тогда
![]() и
и ![]()
Из рис.1 имеем:
![]()
Первый из этих трех интегралов — момент инерции относительно центральной оси Оу. Второй — статический момент относительно той же оси; он равен нулю, так как ось у проходит через центр тяжести фигуры. Наконец, третий интеграл равен площади фигуры F. Таким образом,
|
(1) |
т. е. момент инерции относительно любой оси равен моменту инерции относительно центральной оси, проведенной параллельно у данной, плюс произведение площади фигуры на квадрат расстояния между осями.
Значит, наша задача теперь свелась к вычислению только центральных моментов инерции; если мы их будем знать, то сможем вычислить момент инерции относительно любой другой оси. Из формулы (1) следует, что центральный момент инерции является наименьшим среди моментов инерции относительно параллельных осей и для него мы получаем:
![]()
Найдем
также центробежный момент
инерции ![]() относительно
осей
относительно
осей ![]() ,
параллельных центральным, если
известен
,
параллельных центральным, если
известен ![]() (Рис.1).
Так как по определению
(Рис.1).
Так как по определению
![]()
где: ![]() ,
, ![]() то
отсюда следует
то
отсюда следует
![]()
Так как два последних интеграла представляют собой статические моменты площади относительно центральных осей Оу и Oz то они обращаются в нуль и, следовательно:
|
(2) |
Центробежный момент инерции относительно системы взаимно перпендикулярных осей, параллельных центральным, равен центробежному моменту инерции относительно этих центральных осей плюс произведение из площади фигуры, на координаты ее центра тяжести относительно новых осей.
2.Внутренние усилия при изгибе.Их дифференциальная зависимость.
Внутренние усилия возникают во всех точках поперечного сечения балки и распределены по неизвестному закону. Не имея возможности определить эти внутренние усилия для каждой точки сечения, заменяем их статически эквивалентными внутренними силовыми факторами, приложенными в центре тяжести поперечного сечения.
Внутренние
силовые факторы определяются из
условия равновесия рассматриваемой
части балки. Однако можем внутренние
силовые факторы найти и непосредственно,
как действие отброшенной левой части
на правую часть. Видно, что часть балки,
нагруженная силой P, стремится изогнуть
рассматриваемую нами правую часть
выпуклостью вниз, а также пытается
произвести срез. Следовательно, в сечении
должны возникнуть поперечная сила ![]() и
изгибающий момент
и
изгибающий момент ![]() .
.
Осуществим
параллельный перенос силы P в центр
тяжести поперечного сечения балки. По
правилам теоретической механики мы
должны добавить момент, равный ![]() (рис.
7.1, б).
(рис.
7.1, б).
При прямом изгибе в поперечном сечении балки возникают два внутренних силовых фактора:
изгибающий
момент,
численно равный алгебраической сумме
моментов всех сил, приложенных к
отбрасываемой части балки,
относительно главной
центральной оси,
проходящей через центр тяжести
рассматриваемого сечения (в рассмотренном
нами случае изгибающий момент равен: ![]() );
);
поперечная
сила,
численно равная алгебраической сумме
всех внешних сил (активных и реактивных),
действующих на отбрасываемую часть
балки (в нашем случае поперечная сила
равна: ![]() ).
).
Поперечный изгиб - изгиб, при котором в поперечном сечении балки возникают и изгибающий момент, и поперечная сила. Если поперечная сила не возникает, изгиб называется чистым изгибом.
При определении внутренних усилий при изгибе пользуются следующими принципами, являющимися следствиями реализации метода сечений:
1. Поперечная сила Q в сечении балки численно равна алгебраической сумме проекций на плоскость сечения всех внешних сил, действующих по одну сторону от сечения.
2. Изгибающий момент МИ, возникающий в поперечном сечении балки, численно равен алгебраической сумме моментов внешних сил, действующих по одну сторону от данного сечения, относительно этого сечения.
Правило знаков:
- поперечная сила в сечении балки считается положительной, если равнодействующая внешних сил, действующих слева от сечения, направлена снизу вверх, а действующих справа от сечения - сверху вниз, и отрицательной - в противоположных случаях;
- изгибающий момент считается положительным, если в рассматриваемом сечении балка изгибается выпуклостью вниз, и отрицательным- в противоположном случае
(рис 11).
![]()
Эпюрой изгибающих моментов МИ или поперечных сил Q называется графическое изображение зависимости соответствующего внутреннего силового фактора от координаты сечения, откладываемой вдоль оси балки.
В соответствии с дифференциальной зависимостью Журавского: |
|
Из этого следует, что на прямолинейном ненагруженном внешней пролетной нагрузкой участке стержня эпюра моментов М прямолинейна, а эпюра поперечных сил Q постоянна (рис. 1.12). |
2. В точке приложения сосредоточенного изгибающего момента эпюра моментов М имеет скачок на величину этого момента, а эпюра поперечных сил О постоянна.В точке приложения сосредоточенного крутящего момента эпюра крутящих моментов Мкр имеет скачок на вепичину этого момента рис. 1.11 ,б). |
3. В точке приложения сосредоточенной поперечной силы эпюра изгибающих моментов имеет излом острием навстречу силе, а эпюра поперечных сил - скачок на величину этой силы. |
В точке приложения сосредоточенной продольной силы эпюра продольных сил А/ также имеет скачок на величину этой силы. |
4. Записываем выражение изгибающих моментов для текущего сечения z в случае изгиба консольной балки, находящейся под действием распре-лйпвнной нагрузки (оис.1.13 а): |
|
уравнение квадратной параболы. |
В соответствии с дифференциальной зависимостью Журавского: |
|
уравнение прямой. |
Таким образом, на участке с распределенной нагрузкой эпюры изгибающих моментов М очерчены по квадратной параболе с выпуклостью навстречу действию распределенной нагрузки, а эпюра поперечных сил Q имеет вид трапеции или треугопьника. И очерчена прямой, наклонной линией АВ, при этом направление наклона (при обходе слева направо) совпадает с направлением q (рис. 1.13 а, б, в). |
|
Рис. 1.13 |
Билет 5.

 татический
момент сечения относительно оси,
проходящей через центр тяжести, равен
нулю.
татический
момент сечения относительно оси,
проходящей через центр тяжести, равен
нулю.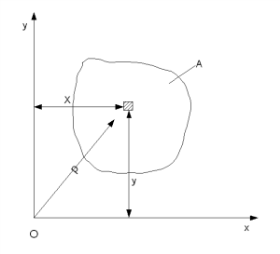 олярный
момент инерции относительно какой –
либо точки равен сумме осевых моментов
инерции относительно двух взаимно
перпендикулярных осей, проходящих
через эту точку.
олярный
момент инерции относительно какой –
либо точки равен сумме осевых моментов
инерции относительно двух взаимно
перпендикулярных осей, проходящих
через эту точку.