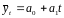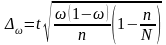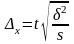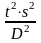- •Тема 1. Предмет и метод статистики
- •Тема 2. Статистическое наблюдение
- •Примеры
- •Тема 3. Сводка и группировка данных
- •Пример 1 (группировка):
- •Пример 2 (вторичная группировка)
- •Тема 4. Статистические показатели. Абсолютные и относительные величины
- •Примеры
- •Тема 5. Средние величины
- •1. Теория средних величин
- •Понятие о средней величине.
- •3. Степенные средние величины
- •Средняя арифметическая
- •Пример 1 (средняя арифметическая простая)
- •Пример 2 (средняя арифметическая взвешенная в дискретных рядах)
- •Пример 3 (средняя арифметическая взвешенная в интервальных рядах)
- •Пример 5 (средняя гармоническая простая)
- •Пример 6 (средняя гармоническая простая).
- •Пример 7 (cредняя гармоническая взвешенная)
- •Пример 8 (cредняя гармоническая взвешенная)
- •Средняя квадратическая и средняя кубическая
- •Пример 9 (средняя квадратическая)
- •Средняя геометрическая
- •Правило мажорантности средних величин
- •4. Структурные средние
- •Пример 12 (структурные средние)
- •Тема 6. Ряды динамики
- •Пример 1
- •Пример 2.
- •Тема 7. Показатели вариации и другие характеристики рядов распределения
- •7.1. Понятие о вариации
- •7.2. Показатели вариации и способы их расчета
- •7.3. Основные свойства дисперсии
- •7.4. Правило сложения дисперсий
- •7.5. Ряды распределения и их моделирование
- •Значение моментов распределения
- •Тема 8. Выборочное наблюдение
- •8.1. Общие сведения о выборочном наблюдении
- •8.2. Виды и схемы отбора
- •8.3. Определение средних и предельных ошибок при различных видах отбора
- •8.4. Определение необходимой численности выборки
- •Тема 9. Индексы
где Qплан и Qбаз – плановый и базисный размеры явления за период.
2. Относительная величина выполнения плана (нормы или договорных обязательств) - результат сравнения фактически достигнутого уровня показателя в текущем (отчетном) периоде с его плановым уровнем или нормативным, или уровнем, обусловленным договором. Если показатели заданы в абсолютном выражении:
 ,
,
где Q факт – фактический объем явления за отчетный период.


 ,
,
Рассмотренные
относительные величины взаимосвязаны
между собой:
 ,
,
4.
Относительная
величина структуры
характеризует состав совокупности,
показывает, какой удельный вес (долю)
во всей совокупности составляют ее
части. Определяется как отношение
размеров частей к целому: d
= (100).
(100).
5. Относительная величина координации – соотношение частей целого между собой. За базу сравнения принимают одну из составных частей целого, а затем находят отношение всех частей к ней. Показывает, сколько единиц данной части целого приходится на 1, 10, 100, 1000 и т.п. единиц части, принятой за базу сравнения:
Kкоординации
= K1
:
K2
:
...
:
K баз
,
 ,
,
где Qбаз – уровень, принятый за базу сравнения; Q1+ Q 2+...+ Qбаз=Qцелое
6. Относительная величина интенсивности характеризует степень распространения или развития какого-либо явления в определенной совокупности, с ним связанной. Получается сопоставлением разноименных абсолютных величин, связанных в своем развитии, но относящихся к различным совокупностям (производительность труда, фондоотдача, рентабельность, демографические коэффициенты, социальные показатели и т.д.)
7. Относительная величина сравнения – отношение одноименных величин, относящихся к разным объектам или территориям, взятое, как правило, за одно и то же время. Выражается в коэффициентах.
Примеры
Пример 1 (условно-натуральный метод) Мыловаренный завод произвел за отчетный период следующее количество продукции, т.:мыло хозяйственное 40%-ное – 25,0; мыло туалетное – 20,0;мыло хозяйственное 60%-ное – 22,0; порошок стиральный – 55,0.Определите общий выпуск продукции в пересчете на условное 40%-ное мыло по следующим переводным коэффициентам: мыло 60%-ное и туалетное – 1,75, порошок стиральный – 0,5.Решение. Перемножив фактический выпуск продукции на коэффициенты пересчета в условное 40%-ное мыло, получим:
25·1.0 + 22.0·1.75 + 20.0·1.75 + 55.0·0.5 = 126 тыс. т условного 40%-ного мыла.
Пример 2 (ОВВП) По плану предусматривалось собрать по 30 ц пшеницы с гектара, а собрано по 33 ц. Определить выполнение плана по урожайности.
Решение. Поделим фактическую урожайность на плановую и получим:(33 100)/30 = 110%
План по урожайности выполнен на 110%, или перевыполнен на 10%.
Пример 3. Планом предприятия предусматривалось повысить производительность труда на 5% и снизить затраты на 2%. Фактически производительность труда возросла на 6%, затраты были снижены на 4%. Определите выполнение плана по росту производительности труда и снижению затрат.
Решение. Степень выполнения плана по повышению производительности труда равна отношению достигнутого уровня - 106% (100% + 6%) к показателю плана - 105% (100% +5%) в процентах:(106 100)/105 = 101%
Аналогично, фактическое снижение затрат - 96% (100% - 4%), а плановое - 98% (100% - 2%) их отношение дает 98%, т.е. план по снижению затрат перевыполнен на 2%.
Пример 4 (ОВС, ОВК) По данным переписи населения 1970 г. в СССР проживало в возрасте 100 лет и старше 19304 чел., из них мужчин 4252 чел., женщин 15052. Определите структуру долгожителей по полу и относительную величину координации, приняв число мужчин за базу, равную 100.
Решение. Для вычисления относительных величин структуры нужно разделить значение каждой части на общий итог, принимаемый за целое (100%). Количество мужчин и женщин в возрасте 100 лет и старше надо поделить на общее их число или исчислить удельный вес мужчин, а затем отнять его от 100%:
(4250 100)/19304 = 22% мужчин
женщин 78% (100%-22%).
Относительные величины координации характеризуют соотношение отдельных частей совокупности. В задаче требуется вычислить соотношение между численностью мужчин и женщин в возрасте 100 лет и старше. Для этого, приняв число мужчин за базу сравнения, равную 100, поделим численность женщин на численность мужчин и получим
(15052 100)/4252 = 354
Это значит, что на каждые 100 мужчин в возрасте 100 лет и старше приходится 354 женщины в том же возрасте.
Пример 5 (ОВИ)
По городу имеются данные за год, тыс.чел.: число родившихся - 24,92; среднегодовая численность населения – 2800. Определить относительную величину интенсивности, характеризующую рождаемость.
Решение
Определим коэффициент рождаемости:
Крожд.
=
 1000
=
1000
= 1000=
90/00.
Это
означает, что в расчете на каждую тысячу
человек населения за год рождается 9
детей.
1000=
90/00.
Это
означает, что в расчете на каждую тысячу
человек населения за год рождается 9
детей.
Тема 5. Средние величины
1. Теория средних величин
Средние величины позволяют сравнивать уровни одного и того же признака в различных совокупностях и находить причины этих расхождений.
В анализе изучаемых явлений роль средних величин огромна. Английский экономист В. Петти (1623—1687 гг.) широко использовал средние величины. В. Петти хотел использовать средние величины в качестве меры стоимости расходов на среднее дневное пропитание одного работника. Устойчивость средней величины – это отражение закономерности изучаемых процессов. Он считал что информацию можно преобразовать, даже если нет достаточного объема исходных данных.
Применял средние и относительные величины английский ученый Г. Кинг (1648—1712) при анализе данных о населении Англии.
Теоретические разработки бельгийского статистика А. Кетле (1796—1874 гг.) основаны на противоречивости природы социальных явлений – высокоустойчивых в массе, но сугубо индивидуальных.
Согласно А. Кетле постоянные причины действуют одинаково на каждое изучаемое явление и делают эти явления похожими друг на друга, создают общие для всех них закономерности.
Следствием учения А. Кетле явилось выделение средних величин в качестве основного приема статистического анализа. Он говорил, что статистические средние величины представляют собой не категорию объективной действительности.
А. Кетле выразил взгляды на среднюю величину в своей теории среднего человека. Средний человек – это человек, обладающий всеми качествами в среднем размере (средняя смертность или рождаемость, средний рост и вес, средняя быстрота бега, средняя наклонность к браку и самоубийству, к добрым делам и т. д.). Для А. Кетле средний человек – это идеал человека. Несостоятельность теории среднего человека А. Кетле была доказана в русской статистической литературе в конце XIX—XX вв.
Известный русский статистик Ю. Э. Янсон (1835—1893 гг.) писал, что А. Кетле предполагает существование в природе типа среднего человека как чего–то данного, от которого жизнь отклонила средних людей данного общества и данного времени, а это приводит его к совершенно механическому взгляду и на законы движения социальной жизни: движение – это постепенное возрастание средних свойств человека, постепенное восстановление типа; следовательно, такое нивелирование всех проявлений жизни социального тела, за которым всякое поступательное движение прекращается.
Сущность данной теории нашла свое дальнейшее развитие в работах ряда теоретиков статистики как теория истинных величин. У А. Кетле были последователи – немецкий экономист и статистик В. Лексис (1837—1914 гг.), перенесший теорию истинных величин на экономические явления общественной жизни. Его теория известна под названием теория устойчивости. Другая разновидность идеалистической теории средних величин основана на философии
Ее основатель – английский статистик А. Боули (1869– 1957гг.) – один из самых видных теоретиков новейшего времени в области теории средних величин. Его концепция средних величин изложена в книге «Элементы статистики».
А. Боули рассматривает средние величины лишь с количественной стороны, тем самым отрывает количество от качества. Определяя значение средних величин (или «их функцию»), А. Боули выдвигает махистский принцип мышления. А. Боули писал, что функция средних величин должна выражать сложную группу с помощью немногих простых чисел. Статистические данные должны быть упрощены, сгруппированы и приведены к средним.
Эти взгляды: разделяли Р. Фишер (1890—1968 гг.), Дж. Юл (1871 – 1951 гг.), Фредерик С. Миллс (1892 г) и др.
В 30—е гг. XX в. и последующие годы средняя величина рассматривается как социально значимая характеристика, информативность которой зависит от однородности данных.
Виднейшие представители итальянской школы Р. Бенини (1862—1956 гг.) и К. Джини (1884—1965 гг.), считая статистику отраслью логики, расширили область применения статистической индукции, но познавательные принципы логики и статистики они связывали с природой изучаемых явлений, следуя традициям социологической трактовки статистики.
В работах К. Маркса и В. И. Ленина средним величинам отводится особая роль.
К. Маркс утверждал, что в средней величине погашаются индивидуальные отклонения от общего уровня и средний уровень становится обобщающей характеристикой массового явления Такой характеристикой массового явления средняя величина становится лишь при условии, если взято значительное число единиц и эти единицы качественно однородны. Маркс писал, чтобы находимая средняя величина была средней «…многих различных индивидуальных величин одного и того же вида».
Средняя величина приобретает особую значимость в условиях рыночной экономики. Она помогает определить необходимое и общее, тенденцию закономерности экономического развития непосредственно через единичное и случайное.
Понятие о средней величине.
Средние величины представляют сводную, обобщенную характеристику статистической совокупности. Она одним числом характеризует все явление, абстрагируясь от случайности индивидуальных значений, и показывает какой размер этого явления приходится на единицу совокупности.
При вычислении средних обобщающих показателей выявляются общие для данной совокупности типические размеры уровня того или иного признака и тем самым выявляются общие для нее типические черты и свойства.
Метод средних величин представляет собой особую форму статистического обобщения. Применение метода средних величин возможно только при наличии вариации признака у совокупности однородных явлений.
Средние величины могут быть как абсолютными, так и относительными (средняя заработная плата, средний процент выполнения плана).
Уровень признака у отдельных единиц совокупности складывается под влиянием разнообразных условий, одни из них являются общими для всех единиц, другие – случайными. В средней величине, исчисленной на основе данных о большом числе единиц, колебания в величине признака, вызванные случайными причинами, погашаются и проявляется общее свойство для всей совокупности. При осреднении все отклонения признака от среднего уровня уравновесились, т.е. произошло отвлечение (абстрагирование) от индивидуальных особенностей отдельных единиц, т.е. средняя величина абстрактна, и в этом заключается ее научная ценность.
Средняя величина правильно характеризует однородные по своему содержанию совокупности. Такая средняя будет типичной, так как она отражает то общее, что характерно для данной совокупности общественных явлений.
Если же совокупность в целом по составу неоднородна, то для получения типичных средних необходимо с помощью метода группировок расчленить такую совокупность на однородные группы и после этого исчислить средние величины для каждой группы отдельно.
Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности.
Объективность и типичность статистической средней могут быть обеспечены лишь при определенных условиях. Первое условие состоит в том, что средняя должна вычисляться для качественно однородной совокупности. Второе условие – для исчисления средней должны быть использованы не единичные, а массовые данные, ибо только тогда взаимопогашаются возможные случайные отклонения.
Следует помнить о том, что чрезмерное увлечение средними показателями может привести к необъективным выводам при проведении анализа. Это связано с тем, что средние величины, будучи обобщающими показателями, погашают, игнорируют те различия в количественных признаках отдельных единиц совокупности, которые реально существуют и могут представлять самостоятельный интерес.
При расчете средних показателей необходимо соблюдать следующие требования:
1) Средние исчисляются только по единицам одного и того же вида и требуют однородности совокупности,
2) Расчет средней и ее значение зависит от времени и от пространства,
3) Осреднение надо сочетать с методом группировок и наряду с общей средней рассчитывать и групповые.
Различают несколько видов и способов расчета средних, но прежде чем выбрать вид и способ расчета средней, необходимо определить экономическое содержание исследуемого показателя, чтобы рассчитать только одно истинное значение средней.
В статистике применяется несколько видов средних величин:
средняя арифметическая;
средняя гармоническая;
средняя квадратическая;
средняя геометрическая;
средняя хронологическая.
Эти средние относятся к классу степенных средних. Кроме них используются структурные средние – мода и медиана.
3. Степенные средние величины
Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными.
Если варианты x встречаются один раз, расчеты проводим по средней простой (например, зарплата 3 тыс. руб. встречается только у одного рабочего и 5 тыс. руб. – у одного рабочего).
Если варианты повторяются неодинаковое число раз, то есть имеет разные частоты f (например, зарплата 3 тыс. рублей встречается у пяти работников и зарплата 5 тыс. руб. – у 4 работников), то расчет проводим по средней взвешенной.
Формула степенной простой в общем виде:

 —
индивидуальное
значение признака
—
индивидуальное
значение признака
![]() -й
единицы совокупности, k—
показатель степени средней величины,
n—
число единиц совокупности
-й
единицы совокупности, k—
показатель степени средней величины,
n—
число единиц совокупности
Формула степенной средней взвешенной в общем виде:

 —
частота
повторения
-й
варианты.
—
частота
повторения
-й
варианты.
При k = -1 - средняя гармоническая; k = 0 - средняя геометрическая;
k = 1 - средняя арифметическая; k = 2 - средняя квадратическая.
Признак,
по которому находится средняя, называется
осредняемым признаком и обозначается
 .
Величины осредняемого признака у каждой
единицы совокупности называются
индивидуальными его значениями или
вариантами. Обозначаются как
x1,
x2,
x3,
…xn..
Частота
(повторяемость) индивидуальных значений
признака – f
(статистический
вес).
.
Величины осредняемого признака у каждой
единицы совокупности называются
индивидуальными его значениями или
вариантами. Обозначаются как
x1,
x2,
x3,
…xn..
Частота
(повторяемость) индивидуальных значений
признака – f
(статистический
вес).
Средняя арифметическая
Cредняя арифметическая - наиболее распространенный вид средней. Она применяется в тех случаях, когда объем осредняемого признака по всей совокупности является суммой значений признаков отдельных ее единиц, например, фонд заработной платы – это сумма заработных плат отдельных рабочих и т. п. При исчислении средней арифметической сумма всех значений признаков делится на их число.
В зависимости от частоты повторения средняя арифметическая делится на два способа расчета:
1. средняя арифметическая простая, не учитывает повторяемость признака и применяется в двух случаях:
- если данные не сгруппированы,
- если данные сгруппированы, но частоты равны.
2. средняя арифметическая взвешенная, применяется в том случае, если частоты неравны.
Расчет средней арифметической взвешенной состоит в следующем:
1) находится произведение признака на частоту по группам,
2) эти произведения суммируются,
3) находится сумма частот,
4) сумма произведения делиться на сумму частот.
В интервальном ряду распределения расчет средней проводится следующим образом:
1) интервальный ряд превращается в дискретный, переходом от двух границ к центру интервала (исчисляется как арифметическая простая из крайних границ);
2) открытые интервалы закрываются по условной длине, равной длине соседнего интервала.
В остальном расчет осуществляется, как и в дискретном ряду.
Средняя арифметическая простая исчисляется путем деления суммы значений признака на число значений.

где
 – средняя арифметическая;
– средняя арифметическая;
x – отдельные значения признака;
n – число значений признака.
Пример 1 (средняя арифметическая простая)
По состоянию на 14 октября имеются следующие данные о расходе металла 8 рабочими (кг): 17,2; 19,0; 20,0; 17,0; 18,0; 19,8; 18,0; 18,6.
Для того чтобы определить средний расход металла на одного рабочего, необходимо общий расход металла разделить на число рабочих:
 кг.
кг.
Если данные представлены в виде дискретного ряда распределения c неравными частотами значений признака, то расчет средней производится по формуле средней арифметической взвешенной:

х – значение признака; f – частота повторения соответствующего признака (веса).
Пример 2 (средняя арифметическая взвешенная в дискретных рядах)
Таблица 5.1.
Затраты времени (сек.) на обработку детали (х) |
Число деталей (f) |
46 |
250 |
48 |
400 |
50 |
150 |
Итого |
800 |
Определить средние затраты времени на обработку детали.
Решение задачи:
 сек.
сек.
Если данные представлены в виде интервального ряда распределения, то принцип расчета средней остается прежним, но предварительно вычисляется среднее значение признака для каждого интервала, представляющее полусумму нижнего и верхнего значений интервала:


![]() –
нижняя
граница интервала;
–
нижняя
граница интервала;
![]() – верхняя граница интервала.
– верхняя граница интервала.
Если есть интервалы с открытыми границами, то для первой группы величина интервала берется равной величине интервала последующей группы.
Пример 3 (средняя арифметическая взвешенная в интервальных рядах)
Известны следующие данные о распределении рабочих предприятия по стажу работы (лет).
Таблица 5.2
-
Стаж работы (x)
Число рабочих (f)
до 5
15
5 – 10
25
10 – 15
12
15 – 20
28
20 и более
20
Определить средний стаж работы одного рабочего.
Решение задачи:
Среднее значение признака из интервального ряда можно определить двумя способами:
по средней арифметической взвешенной:

В этой формуле за величину x принимается средняя интервала в каждой группе.
методом моментов:

Момент первого порядка определяется так:

А - постоянная величина, за которую принимается варианта (середина интервала) находящаяся в центре ряда.
i - величина интервала.
Способы расчета представим в следующей таблице.
Таблица 5.3
Стаж работы, лет (x) |
Число рабочих, чел (f) |
Cередина
интервала
|
|
|
|
до 5 |
15 |
(0+5)/2=2,5 |
-10 |
-2 |
-30 |
5 -10 |
25 |
(5+10)/2=7,5 |
-5 |
-1 |
-25 |
10 - 15 |
12 |
(10+15)/2=12,5 |
0 |
0 |
0 |
15 - 20 |
28 |
(15+20)/2=17,5 |
+5 |
+1 |
+28 |
20 и более |
20 |
(20+25)/2=22,5 |
+10 |
+2 |
+40 |
Итого |
100 |
|
|
|
13 |
I способ расчета:
 года
года
II способ расчета:
Подставив данные таблицы в формулы, получим:
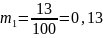 и
и
 года
года
Оба способа расчета дали одинаковый результат.
Пример 4 (свойства средней величины)
Все частоты уменьшились в два раза, а все варианты увеличились на две единицы. Что произойдет со средней?
Решение. Согласно свойствам средней арифметической, если все частоты ряда уменьшить или увеличить в одинаковое количество раз, то средняя не изменится, т.е. с точки зрения частот средняя не изменится. Если все варианты увеличить или уменьшить на одно и то же число, то и средняя изменится на это же число. В нашем случае средняя увеличится на две единицы.
Средняя гармоническая
Средняя гармоническая – это величина, обратная средней арифметической. Применяется, если заданы объемы явлений (объемы признаков), но не известны частоты. По способу расчета средняя гармоническая бывает:
 -
простая,
применяется, когда объемы признака (n)
равны.
-
простая,
применяется, когда объемы признака (n)
равны.
 -
взвешенная,
применяется, когда известны индивидуальные
значения признака (х),
но не заданы веса (f),
которые входят сомножителем в известный
объемный показатель (М
= х f).
-
взвешенная,
применяется, когда известны индивидуальные
значения признака (х),
но не заданы веса (f),
которые входят сомножителем в известный
объемный показатель (М
= х f).
В практической работе часто возникает задача выбора формы средней величины между средней арифметической взвешенной и средней гармонической взвешенной. Для этого необходимо составить исходную схему расчета показателя ():
 .
.
Например, ;
;

Если в условии задачи известен знаменатель исходной схемы, а неизвестен числитель, то применяется средняя арифметическая взвешенная.
Если известен числитель, а знаменатель – нет, то используется средняя гармоническая взвешенная.
Пример 5 (средняя гармоническая простая)
Бригада токарей была занята обточкой одинаковых деталей в течение 8-часового рабочего дня. Первый токарь затратил на одну деталь 12 мин, второй – 15 мин., третий – 11, четвертый – 16 и пятый – 14 мин. Определите среднее время, необходимое на изготовление одной детали.
Решение задачи:
На первый взгляд, кажется, что задача легко решается по формуле средней арифметической простой:
![]()
Полученная средняя была бы правильной, если бы каждый рабочий сделал только по одной детали. Но в течение дня отдельными рабочими было изготовлено различное число деталей.
Число деталей, изготовленных каждым рабочим, определяется отношением всего времени работы к среднему времени, затраченному на одну деталь. Тогда среднее время, необходимое для изготовления одной детали, равно:

Это же решение можно представить иначе:

Пример 6 (средняя гармоническая простая).
Три предприятия производят одинаковые товары. Себестоимость одного товара составляет: на 1-ом предприятии 50 руб., на 2-ом 60 руб., на 3-ем 80 руб. Определить среднюю себестоимость товара при условии, что общие затраты на производство товара на всех предприятиях одинаковы.
Решение задачи:
Составим исходную схему расчета (исходное соотношение):
 .
.
Так как общие затраты на всех предприятиях одинаковы, а значения признака (себестоимости) известны (x), расчет выполняем по средней гармонической простой:
 =
60,6 руб.
=
60,6 руб.
Пример 7 (cредняя гармоническая взвешенная)
Средняя выработка продукции на одного рабочего за смену в двух цехах завода, вырабатывающих однородную продукцию, характеризуется следующими данными:
Таблица 5.4
Бригада № |
Цех № 1 |
Бригада № |
Цех № 2 |
||||
дневная выработка продукции, шт |
число рабочих, чел |
дневная выработка продукции, шт |
объем произведенной продукции,шт. |
||||
I |
20 |
8 |
IV |
38 |
418 |
||
II |
30 |
11 |
V |
36 |
432 |
||
III |
35 |
16 |
VI |
20 |
140 |
||
Определить среднюю дневную выработку продукции рабочих по каждому цеху.
Решение задачи:
Логическое исходное соотношение:

По первому цеху расчет произведем по средней арифметической взвешенной, поскольку по условию задачи известен знаменатель логической схемы расчета, т. е. число рабочих или частота появления признака:
 шт.
шт.
По второму цеху – по средней гармонической взвешенной, т.к. известен числитель логической схемы расчета, т.е объем произведенной продукции, и не известен знаменатель – число рабочих:
 шт.
шт.
Пример 8 (cредняя гармоническая взвешенная)
Автомобиль проехал 1000 км, из них 480 км он прошел со скоростью 60 км/час, 320 со скоростью 80 км/час и 200 км со скоростью 50 км/час. Определите среднюю скорость, с которой совершался рейс.
Решение задачи:
Логическое исходное соотношение:
 ,
,
В этой задаче опять известны только значения признака, а значения частот (время) не даны, однако имеются данные о пройденном расстоянии, которое является произведением признака на частоту. В этом случае средняя рассчитывается по формуле средней гармонической взвешенной:
 ,
,
Средняя квадратическая и средняя кубическая
В ряде случаев в экономической практике возникает потребность расчета среднего размера признака, выраженного в квадратных или кубических единицах измерения. Тогда применяется средняя квадратическая (например, для вычисления средней величины стороны квадратных участков, средних диаметров труб, стволов и т.п.) и средняя кубическая (например, при определении средней длины стороны кубов).
Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, то средняя будет являться квадратической средней величиной.
Средняя квадратическая простая является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:

где
![]() ,
,![]() ,…
,…![]() - значения признака, n- их число.
- значения признака, n- их число.
Средняя квадратическая взвешенная:
 ,
где
,
где
![]() -
веса.
-
веса.
Средняя кубическая простая является кубическим корнем из частного от деления суммы кубов отдельных значений признака на их число:
 ,
,
где , ,… - значения признака, n- их число.
Средняя кубическая взвешенная:
 ,
,
где - веса.
Средняя квадратическая и средняя кубическая необходимы для расчета средних значений, когда исходные данные представлены в квадратных или кубических единицах измерения.
Пример 9 (средняя квадратическая)
Имеются
три участка земельной площади со
сторонами квадрата:
 = 100 м;
= 100 м;
 =
200 м;
=
200 м;
 =300 м. Определить среднюю сторону квадрата
(участка).
=300 м. Определить среднюю сторону квадрата
(участка).
Решение задачи:
Заменяя разные значения длины сторон на среднюю, мы, очевидно, должны исходить из сохранения общей площади всех участков.
Арифметическая средняя величина (100+200+300)/3 =200 м не удовлетворяет этому условию, так как общая площадь трех участков со стороной 200 м была бы равна: 3· .
В то же время площадь исходных трех участков равна:
 .
.
Правильный ответ дает квадратическая средняя:
 м.
м.
Средняя геометрическая
Используется для осреднения относительных величин. Чаще всего используется для определения средних коэффициентов роста, темпов роста и темпов прироста. Средняя геометрическая равна корню степени m из произведений относительных величин, чаще всего, коэффициентов роста. (m - число коэффициентов роста),
 ,
,
где П – знак произведения.
Средний
коэффициент роста (среднюю геометрическую)
можно определить и по значениям первого
и последнего членов динамического ряда.
Если первый уровень ряда обозначить
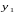 ,
а последний -
,
а последний -
 ,
то
,
то
 ,
,
где n - число уровней ряда (число лет).
Средняя из средних коэффициентов или темпов роста за неодинаковые промежутки времени рассчитывается по формуле средней геометрической взвешенной, причем весами являются сами промежутки времени, следовательно:

Пример 10 (средняя геометрическая)
Определите среднегодовой темп роста выпуска продукции на заводе, если в 1990 г. было произведено продукции на 21,15 тыс. у.е., а в 1995 г. было запланировано произвести продукции на 35 тыс.у.е.
Решение задачи:
Для определения средних темпов роста применяется средняя геометрическая. Когда имеются данные о первом периоде (в нашем случае выпуск продукции в 1990 г. на сумму 21,15 тыс.у.е.) и в последнем периоде (в задаче — выпуск продукции по плану в 1995 г. на сумму тыс.35 у.е.), среднегодовой темп роста определяется по формуле:

Пример 11 (средняя геометрическая)
Среднегодовой темп роста заработной платы рабочих завода за 1990-91 гг. составил 104%, а за 1992-1994 гг. -106%. Определить среднегодовой темп роста заработной платы на заводе за 1990 1994 гг.
Решение задачи:
Средняя из средних темпов роста за неодинаковые промежутки времени рассчитывается по формуле средней геометрической взвешенной, причем весами являются сами промежутки времени, следовательно:

Примеры на использование данной формулы рассматриваются также в теме «Ряды динамики»
Правило мажорантности средних величин
Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени m увеличивается и соответствующая средняя величина:
![]()
Все
выше рассмотренные виды средних величин
можно получить из формулы степенной
средней вида

При различных значениях показателя получаются различные средние: средняя арифметическая, гармоническая, геометрическая и квадратическая.
Мажорантность средних состоит в том, что средняя некоторого вида всегда больше средней некоторого другого вида (для признака, не могущего иметь отрицательных значений). В частности, если для одной совокупности вычислить средние гармоническую, геометрическую, арифметическую и квадратическую, то по численному значению они расположатся в возрастающем порядке. Порядок возрастания этих средних определяет показатель степени k в формуле степенной средней, т.е. чем больше k, тем больше средняя (табл 5.5).
Таблица 5.5
Порядок возрастания средних
k |
-1 |
0 |
1 |
2 |
Название средней |
гармоническая |
геометрическая |
арифметическая |
квадратическая |
Подробно общее условие мажорантности т.е. соотношения между различными видами средних было сформулировано А. Я. Боярским.
4. Структурные средние
К
ним относятся медиана ( ),мода
(
),мода
( ),
квартили (
),
квартили ( ),
децили (
),
децили (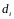 )
и перцентили (
)
и перцентили ( )
распределения.
)
распределения.
Медиана – это величина варьирующего признака, которая делит ряд распределения на две равные части, т.е. медиана соответствует варианте, стоящей в середине ряда.
Медиана определяется в зависимости от вида ряда распределения:
в ранжированном ряду с нечетным числом уровней медиана соответствует признаку с порядковым номером:
 ,
,
где n - объем совокупности.
в ранжированном ряду с четным числом значений варьирующего признака (
 ;
; )
за медиану условно принимают значение:
)
за медиану условно принимают значение:

в дискретном ряду распределения медиана соответствует варианте, для которой первая накопленная частота больше половины общего числа наблюдений;
в интервальном ряду распределения медианным интервалом будет интервал, для которого первая накопленная частота больше половины объема совокупности, а сама медиана определяется по формуле:
 ,
,
где -
нижняя граница медианного интервала;
-
нижняя граница медианного интервала; -
величина медианного интервала;
-
величина медианного интервала; -
частота медианного интервала;
-
частота медианного интервала;
 -
накопленная частота до медианного
интервала.
-
накопленная частота до медианного
интервала.
Графически медиана определяется по кумуляте распределения.
Мода - наиболее часто встречающийся признак в совокупности. Определяется:
в дискретном ряду – по максимальной частоте;
в интервальном ряду модальный интервал определяется по максимальной частоте, а сама мода - по формуле:
 ,
,
где
 -
нижняя граница модального интервала;
-
нижняя граница модального интервала;
 -
величина модального интервала;
-
величина модального интервала; -
частота модального интервала;
-
частота модального интервала; -
частота интервала, предшествующего
модальному;
-
частота интервала, предшествующего
модальному; -
частота интервала, следующего за
модальным.
-
частота интервала, следующего за
модальным.
Графически мода определяется на основе полигона распределения (для дискретного вариационного ряда) или гистограммы распределения (для интервального вариационного ряда).
Значения
признака, делящие совокупность на четыре
равные части, называются квартилями
и обозначаются буквой Q
с
подписным значком номера квартиля, -
ясно, что Q2
совпадает с медианой, т.е. Q2
=
= М
е.
Первый (Q1)
и третий (Q3)
квартили определяются по следующим
формулам: ;
; ,
,
где
хQ1,хQ3-
нижняя граница, соответственно, первого
и третьего квартильных интервалов;
hQ1,
hQ3-
величина соответствующего первого и
третьего квартильных интервалов;
fQ1,
fQ3
-
частота соотвествующих квартильных
интервалов; -
накопленная частота до первого
квартильного интервала;
-
накопленная частота до первого
квартильного интервала; -
накопленная частота до третьего
квартильного интервала.
-
накопленная частота до третьего
квартильного интервала.
Децили
– варианты, делящие ряд распределения
на десять равных частей. Вычисляются
они по той же схеме, что и медиана, и
квартили: ;
; и т.д
и т.д
Значения
признака, делящее ряд на сто частей,
называются перцентилями, и их расчет
выполняется аналогично исчислению
децилей и квартилей. Анализ вариационного
ряда дополняется определением показателей
дифференциации и концентрации. Например,
коэффициент децильной дифференциации: ,
,
где d9 – девятая дециль, или девятый дециль; d1 – первая дециль, или первый дециль.
Он показывает, во сколько раз наименьший уровень признака из 10% признаков, имеющих наибольший уровень, больше наибольшего уровня признака из 10% единиц совокупности, имеющих наименьший уровень признака.
Коэффициент
фондов (Кф)–
это соотношение между средними значениями
изучаемого признака (или суммарными их
значениями) в десятой и первой децильных
группах, - рассчитывается по формуле: .
.
Пример 12 (структурные средние)
Распределение семей по среднедушевым доходам следующее:
Таблица 5.6
Распределение семей по среднедушевому доходу
Среднедушевые доходы в год, тыс. руб. |
Число семей |
Закрытые интервалы среднедушевых доходов, тыс. руб. |
|
х |
xf |
1 |
2 |
3 |
4 |
5 |
6 |
До 150,0 |
10 |
130 - 150 |
10 |
140 |
1400 |
150,0 -170,0 |
20 |
150 - 170 |
30 |
160 |
3200 |
170,0 -190,0 |
40 |
170 - 190 |
70 |
180 |
7200 |
190,0 -210,0 |
50 |
190 - 210 |
120 |
200 |
10000 |
210,0 -230,0 |
30 |
210 - 230 |
150 |
220 |
6600 |
230,0 -250,0 |
25 |
230 - 250 |
175 |
240 |
6000 |
Свыше 250,0 |
25 |
250 - 270 |
200 |
260 |
6500 |
Итого |
200 |
|
|
|
40900 |
Определите структурные характеристики распределения семей по размеру среднедушевого дохода.
Решение задачи:
Определяем структурные характеристики ряда распределения.
Для
выбора соответствующего интервала
предварительно определим накопленные
частоты
 .
.
Модальный
интервал – это интервал с наибольшей
частотой
 ,
,
тогда:
 тыс.
руб.
тыс.
руб.
Большинство семей имеют среднедушевые доходы в размере 196,67 тыс. руб.
Медианным
является интервал
 ,
т.к. для него первая накопленная частота
больше половины объема совокупности,
т.е.
120100.
,
т.к. для него первая накопленная частота
больше половины объема совокупности,
т.е.
120100.
Тогда медиана будет равна:
 тыс.
руб.
тыс.
руб.
Половина семей имеют среднедушевые доходы, не превышающие доходы 202 тыс. руб., а у другой половины семей среднедушевые доходы, соответственно, выше 202 тыс. руб.
Интервал,
в котором будет находиться первый
квартиль( )
распределения,
)
распределения,
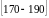 ,
т.к. ему соответствует первая накопленная
частота
,
т.к. ему соответствует первая накопленная
частота
![]() ,
большая
,
большая
 ;
а интервал, в котором находится третий
квартиль(
;
а интервал, в котором находится третий
квартиль( ),
будет
),
будет ,
т.к. ему соответствует
,
т.к. ему соответствует
![]() >
>
 .
.
Тогда соответствующие квартили будут равны:
 тыс.
руб;
тыс.
руб;
 тыс.
руб.
тыс.
руб.
Среднедушевые доходы, не превышающие 180 тыс. руб., получают не менее четверти (25%) из всей совокупности семей, а в размере, не превышающем 230тыс. руб., не менее 75% всех семей.
Более
детальная характеристика распределения
может быть получена на основе децилей
распределения. Интервалы соответствующих
децилей определяются аналогично по
соответствующим накопленным частотам.
Например, находим первую ,
- это будет
,
- это будет
 ;
тогда соответствующий ей интервал
;
тогда соответствующий ей интервал
 будет
тем интервалом, в котором находится
первый дециль (d1)
– и т.д.
будет
тем интервалом, в котором находится
первый дециль (d1)
– и т.д.
Рассчитаем соответствующие децили:
 тыс.
руб.;
тыс.
руб.;
 тыс.
руб;
тыс.
руб;
 тыс.
руб;
тыс.
руб;
 тыс.
руб;
тыс.
руб;
 тыс.
руб.;
тыс.
руб.;
 тыс.
руб;
тыс.
руб;
 тыс.
руб;
тыс.
руб;
 тыс.
руб;
тыс.
руб;
 тыс.
руб.
тыс.
руб.
Первый дециль показывает, что у 10% семей с самым низким среднедушевым доходом самый высокий размер среднедушевого дохода составляет 160 тыс. руб., а девятый дециль, - что среди 10% семей с самым высоким уровнем дохода – нижняя его граница составляет 254 тыс. руб.
Тема 6. Ряды динамики
Рядом динамики называется ряд чисел, характеризующих изменение явления во времени.
В зависимости от того, выражают уровни ряда состояние явления на определенные моменты времени (на начало месяца, квартала, года и т.п.) или его величину за определенные интервалы времени (за сутки, декаду, месяц, год и т.п.) различают соответственно моментные и интервальные ряды динамики.
Уровни ряда динамики могут выражаться абсолютными, относительными и средними величинами.
Для анализа изменения социально-экономических явлений во времени применяются следующие показатели: абсолютный прирост, темп роста, темп прироста, абсолютное содержание 1% прироста. Их определяют базисным, цепным способами и осредняют.
Таблица 6.1
Формулы показателей анализа ряда динамики
Показатели |
Способ расчета |
|
базисный |
цепной |
|
Абсолютный прирост |
|
|
Темп роста |
|
|
Темп прироста |
|
|
Абсолютное содержание 1% прироста |
- |
|
Условные обозначения: уi - уровень текущего периода; уi-1- уровень периода, предшествующего текущему; уб - базисный уровень (первый в ряду динамики).
В оценке динамики явлений большое значение имеют расчеты средних аналитических показателей, которые являются обобщающей характеристикой уровней, их абсолютной скорости и интенсивности изменения.
Методы расчета среднего уровня ряда динамики зависят от его вида и способов получения статистических данных.
В
интервальном ряду
динамики с равностоящими во времени
уровнями расчет среднего уровня ( )
производится по формуле средней
арифметической простой:
)
производится по формуле средней
арифметической простой:

где n – количество хронологических дат.
Если интервальный ряд динамики имеет не равноотстоящие уровни, то средний уровень вычисляется по формуле:

где t – количество периодов времени, в течение которых уровень не изменяется.
В моментных рядах динамики существует следующие варианты расчета среднего уровня:
1) дан ряд с равными интервалами времени между датами:

2) дан ряд с разными интервалами времени между датами и неизвестным характером изменений уровней между датами:

где
 -
средний уровень явления между двумя
соседними датами.
-
средний уровень явления между двумя
соседними датами.

где
 -
начальный и конечный уровни на і-м
интервале;
-
начальный и конечный уровни на і-м
интервале;
 -
длительность интервала времени между
двумя соседними датами.
-
длительность интервала времени между
двумя соседними датами.
3) дан ряд с неравными интервалами времени между датами, но с исчер-пывающими данными об изменении явления между теми же датами:

где yi – размер явления, который оставался неизменным в течение ti интервала времени.
Средний абсолютный прирост определяется по формуле:

где
 - конечный уровень ряда.
- конечный уровень ряда.
Средний темп роста рассчитывается по средней геометрической:

Средний темп прироста вычисляется так:
 или
или

Среднее абсолютное содержание 1% прироста рассчитывается по формуле:

Одной из причин неверного отражения динамики явления слу-жит несопоставимость уровней ряда. Устранение несопоставимости уровней динамических рядов достигается использованием специальных приемов.
Смыкание рядов динамики применяется в случае несопоставимости уровней по территории, по кругу охватываемых объектов, по методике расчета показателей и др. Смыкание осуществляется двумя методами.
1. Использование коэффициентов пересчета. За год, когда возникла несопоставимость уровней, рассчитывается коэффициент, показывающий во сколько раз один уровень больше или меньше другого. Умножая на полученный коэффициент уровни ряда до изменения, приводят их к виду, сопоставимому с последующими уровнями.
2. Замена абсолютных уровней относительными, выраженными в базисных темпах роста. При этом уровень ряда за год, общий для сравниваемых рядов, принимается за 100%. Остальные уровни пересчитываются по отношению к этой базе сравнения, и получается новый ряд динамики, состоящий из относительных показателей.
При изучении рядов динамики возникает необходимость получения сравнительных характеристик направления и интенсивности роста одновременно развивающихся во времени явлений. Это достигается путем приведения рядов динамики к общему основанию. В этом случае данные о величине изучаемого показателя за год, принятый за базисный, принимают в каждом ряду за 100%, а уровни остальных лет относят к нему, получая базисные темпы роста.
Для оценки роста показателей сравниваемых параллельных рядов динамики за один и тот же период времени рассчитывают коэффициент опережения.
Его исчисляют как отношение базисных темпов роста (или средних годовых темпов роста) за одинаковые отрезки времени по двум динамическим рядам:
 или
или

где
 ,
, -
соответственно базисные и средние
годовые темпы роста одного ряда динамики;
-
соответственно базисные и средние
годовые темпы роста одного ряда динамики;
 ,
, -
соответственно базисные и средние
годовые темпы роста второго ряда
динамики.
-
соответственно базисные и средние
годовые темпы роста второго ряда
динамики.
При этом в качестве первого ряда динамики берется тот ряд, темпы роста для которого выше.
Для характеристики скорости изменения уровней одного и того же ряда динамики за отдельные периоды времени определяют коэффициент ускорения (замедления). По аналогии с коэффициентом опережения он рассчитывается на основании базисных или средних годовых темпов роста:


где
 ,
, -
базисные темпы роста уровней ряда
динамики соответственно за второй и
первый периоды одного и того же ряда
динамики;
-
базисные темпы роста уровней ряда
динамики соответственно за второй и
первый периоды одного и того же ряда
динамики;
 ,
, -
средние годовые темпы роста соответственно
за второй и первый периоды одного и того
же ряда динамики.
-
средние годовые темпы роста соответственно
за второй и первый периоды одного и того
же ряда динамики.
Важной задачей статистики при анализе рядов динамики является определение основной тенденции развития.
Основными показателями, дающими представление о тенденции (тренде) развития явления во времени, являются цепные абсолютные приросты, цепные темпы роста и средние уровни.
Если расчет цепных показателей не позволил выявить тенденцию в ряду динамики, то переходят к обработке ряда с помощью методов, основанных на расчете средних уровней. К таким методам относятся: укрупнение интервалов времени, эмпирическое сглаживание (метод скользящей средней) и аналитическое выравнивание.
Укрупнение интервалов времени. Суть метода укрупнения интервалов времени в динамических рядах состоит в том, что берут данные за промежутки времени большей длительности по сравнению с первоначальными. Например, суточные данные заменяют пятидневными, декадными, месячными; месячные – квартальными, годовыми; годовые – трех-, четырех-, пятилетними и т.д. Укрупнение интервалов следует начинать с наименьшего возможного, т.е. интервала, объединяющего два уровня. В случае, если укрупнение по два уровня не дает возможности увидеть тенденцию, переходят к следующему возможному интервалу.
Сущность метода скользящей средней заключается в замене абсолютных уровней средними арифметическими за определенные периоды. При этом расчет средних ведется способом скольжения, т.е. постепенным исключением из принятого периода скольжения первого уровня и включением следующего.
Наиболее
эффективным способом выявления основной
тенденции развития является аналитическое
выравнивание.
При этом уровни ряда динамики выражаются
в виде функции времени: .
Аналитическое выравнивание может быть
осуществлено по любому рациональному
уравнению тренда. Выбор формы уравнения
производится на основе анализа характера
закономерностей динамики изучаемого
явления. В таблице 6.2 приведены системы
уравнений, которые необходимо решить
для определения параметров уравнений,
описывающих тенденции в рядах динамики.
.
Аналитическое выравнивание может быть
осуществлено по любому рациональному
уравнению тренда. Выбор формы уравнения
производится на основе анализа характера
закономерностей динамики изучаемого
явления. В таблице 6.2 приведены системы
уравнений, которые необходимо решить
для определения параметров уравнений,
описывающих тенденции в рядах динамики.
Таблица 6.2
Уравнения, используемые при аналитическом
выравнивании динамических рядов
Вид уравнения |
Системы уравнений |
|
Обычный способ рас- чета параметров |
Упрощенный способ расчета параметров |
|
Прямая:
|
|
|
Парабола второго порядка:
|
|
|
Показательная
кри-вая: |
|
|
Гипербола:
|
|
|
При
анализе рядов динамики в ряде случаев
возникает необходимость в выявлении
сезонных
колебаний.
Для определения сезонных колебаний
обычно анализируются месячные и
квартальные уровни ряда динамики за
год или за несколько лет (в основном не
менее 3-х лет). При выявлении и оценке
сезонности рассчитывают специальные
показатели – индексы сезонности ( ).
Способы определения индексов сезонности
различны и зависят от характера ряда
динамики.
).
Способы определения индексов сезонности
различны и зависят от характера ряда
динамики.
В
рядах, не имеющих ярко выраженной
тенденции развития (или она не наблюдается
совсем), изучение сезонности основано
на методе
простой средней. Сущность
этого метода заключается в том, что
показатели сезонной волны определяются
процентным отношением соответствующих
средних месячных (квартальных уровней)
к их общей средней за весь изучаемый
период. Следовательно, при изучении
помесячной сезонности сначала средние
по месяцам и среднюю годовую исчисляют
из данных за несколько лет (по простой
арифметической), а затем эти средние по
месяцам года ( )относят
к средней годовой (к среднему месячному
уровню для взятых лет) (
)относят
к средней годовой (к среднему месячному
уровню для взятых лет) ( ),
т.е. индекс сезонности исчисляется по
формуле:
),
т.е. индекс сезонности исчисляется по
формуле:

В рядах динамики, имеющих тенденцию развития, для определения индексов сезонности вначале рассчитывают уровни, сглаженные методом скользящей средней или выравненные по определенной функции.
Индексы
сезонности вычисляются отношением
фактического уровня за определенный
квартал или месяц ( )
к выравненному за этот же период (
)
к выравненному за этот же период ( ).
В результате при использовании, например,
квартальных данных за три года получают
двенадцать индексов сезонности:
).
В результате при использовании, например,
квартальных данных за три года получают
двенадцать индексов сезонности:
 .
.
Затем исчисляют средние индексы сезонности для одноименных кварталов за рассматриваемые годы:
 .
.
Пример 1
Рассчитать следующие показатели анализа рядов динамики: цепные и базисные абсолютные приросты, коэффициенты, темпы роста и прироста, абсолютное значение одного процента прироста, а также средние показатели ряда динамики.
Таблица 6.3
годы |
1992 |
1993 |
1994 |
1995 |
1996 |
выплавка стали (тыс. т) |
1160 |
1210 |
1260 |
1310 |
1360 |
Решение задачи:
Рассчитанные аналитические показатели изложили в табличной форме:
Показатели |
1992 |
1993 |
1994 |
1995 |
1996 |
Выплавлено стали (тыс. т) |
1160 |
1210 |
1260 |
1310 |
1360 |
Абсолютные приросты (тыс.т) цепные (по сравн. с пред. год.) |
- |
+50 |
+50 |
+50 |
+50 |
базисные (по сравн. с 1990) |
- |
+50 |
+100 |
+150 |
+200 |
Коэффициенты роста цепные (по сравн. с пред. год.) |
1 |
1,043 |
1,041 |
1,039 |
1,038 |
базисные (к 1990г.) |
1 |
1,043 |
1,086 |
1,129 |
1,172 |
Темпы роста (в %) цепные |
100 |
104,3 |
104,1 |
103,9 |
103,8 |
базисные |
100 |
104,3 |
108,6 |
112,9 |
117,2 |
Темпы прироста (в %) цепные |
- |
+4,3 |
+4,1 |
+3,9 |
+3,8 |
базисные |
- |
+4,3 |
+8,6 |
+12,9 |
+17,2 |
Абсолютное содержание одного процента прироста (т. т) |
- |
1,16 |
1,21 |
1,26 |
1,31 |
Средний абсолютный прирост:

 тыс.т
тыс.т
Средний коэффициент определяется по формуле средней геометрической:
 К
=
К
=
 или
К =
или
К =
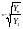
К
=

К
=

Средний темп роста:
__ __ __
Т = К * 100 Т = 1,04 * 100 = 104 %
Средний темп прироста:
_ __ _
t = T - 100 t = 104 - 100 = 4 %.
Пример 2.
Имеются данные об урожайности ячменя за 1988 - 1996гг. (ц).
1988 |
1989 |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
10 |
10,7 |
12 |
10,3 |
12,9 |
16,3 |
15,6 |
17,8 |
18 |
Выявить основную тенденцию урожайности за 1988 - 1996 гг.: 1) методом сглаживания ряда с помощью скользящей средней; 2) методом аналитического выравнивания по уравнению прямой.
Решение задачи:
МЕТОД СГЛАЖИВАНИЯ РЯДА ДИНАМИКИ СКОЛЬЗЯЩЕЙ СРЕДНЕЙ. Сгладим ряд динамики по трехлетней скользящей средней, так как период колебаний продажи равен трем годам.
Исчислим:
средний уровень за 1988 - 1990 гг.
__
У1
 (ц)
(ц)
Средний уровень за 1989 - 1991 гг.
У2
 (ц)
(ц)
Средний уровень за 1990 - 1992 гг.
У3
 (ц)
и т.д.
(ц)
и т.д.
Результаты расчета трехлетней скользящей средней представлены в нижеследующей таблице:
|
годы |
Скользящая трехлетняя |
Трехлетняя скользящая средняя |
А |
1 |
2 |
3 |
1988 |
10,0 (У1) |
- |
- |
1989 |
10,7 (У2) |
32,7 (У1 + У2 + У3) |
10,9 (У1) |
1990 |
12,0 (У3) |
33,0 (У2 + У3 + У4) |
11,0 (У2) |
1991 |
10,3 (У4) |
35,2 (У3 + У4 + У5) |
11,8 (У3) |
1992 |
12,9 (У5) |
39,5 (У4+ У5 + У6) |
13,2 (У4) |
1993 |
16,3 (У6) |
44,8 (У5 + У6 + У7) |
14,9 (У5) |
1994 |
15,5 (У7) |
49,7 (У6 + У7 + У8) |
16,6 (У6) |
1995 |
17,8 (У8) |
51,4 (У7 + У8 + У9) |
17,1 (У7) |
1996 |
18,0 (Уn) |
- |
- |
Полученные результаты (гр. 3) характеризуют рост урожайности.
МЕТОД АНАЛИТИЧЕСКОГО ВЫРАВНИВАНИЯ РЯДА ДИНАМИКИ ПО ПРЯМОЙ.
Уравнение прямой линии выражено формулой:
Уt = a0 +a1t
где Уt - значение выравненного ряда, которые нужно вычислить (теоретические уровни);
a0 и a1 - параметры прямой;
t - показатель времени (дни, месяцы, годы и т.д.)
Для нахождения параметров a0 и a1 необходимо решить систему нормальных уравнений:
a0 n + a1t = у
a0 t + a1t2 = уt ,
где у - фактические уровни ряда динамики;
n - число уровней.
Для упрощения расчетов обозначим время так, чтобы начало отсчета времени приходилось на середину рассматриваемого периода:
Годы |
1988 |
1989 |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
t |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
Следовательно, t = 0. тогда система нормальных уравнений примет вид:
a0 n = у
a1t2 = уt ,
Отсюда
a0
 ;
a1
;
a1
 .
.
Расчет параметров a0 и a1
Годы |
Урожайность в ц с 1 га |
Условные годы , t |
t2 |
уt |
уt |
A |
1 |
2 |
3 |
4 |
5 |
1988 |
10,0 |
-4 |
16 |
-40,0 |
9,30 |
1989 |
10,7 |
-3 |
9 |
-32,1 |
10,41 |
1990 |
12,0 |
-2 |
4 |
-24,0 |
11,52 |
1991 |
10,3 |
-1 |
1 |
-10,3 |
12,63 |
1992 |
12,9 |
0 |
0 |
0 |
13,74 |
1993 |
16,3 |
1 |
1 |
16,3 |
14,85 |
1994 |
15,6 |
2 |
4 |
31,2 |
15,96 |
1995 |
17,8 |
3 |
9 |
53,4 |
17,07 |
1996 |
18,0 |
4 |
16 |
72,0 |
18,18 |
|
у = 123,6 |
t = 0 |
t2 = 60 |
+172,9 - 106,4 = ------------ уt = 66,5 |
уt = 123,66 |
Следовательно,
a0
 (руб.);
(руб.);
a1
 (руб.)
.
(руб.)
.
Таким образом, уравнение прямой имеет вид:
уt = 13,74 + 1,11 * t
Подставив в это уравнение значение t (гр.2), получим выравненные теоретически значения уt (гр.5).
Тема 7. Показатели вариации и другие характеристики рядов распределения
7.1. Понятие о вариации
При изучении процессов и явлений общественной жизни статистика встречается с разнообразной вариацией признаков, характеризующей отдельные единицы совокупности. Величина признака изменяется, колеблется под влиянием различных причин и условий. Чем разнообразнее условия, влияющие на размер данного признака, тем больше его вариация.
Таблица 7.1
Дневная выработка рабочих двух бригад
Номер бригады |
Число рабочих |
Дневная выработка деталей отдельных рабочих, шт. |
Средняя дневная выработка |
1 |
6 |
75 90 78 82 93 86 |
84 |
2 |
6 |
65 122 84 70 105 58 |
84 |
Одна и та же средняя может характеризовать совокупность, в которой размеры вариации признака существенно отличаются друг от друга (табл.5.1). Как видно, средняя дневная выработка в обеих бригадах одинакова, хотя в первой бригаде средняя значительно меньше отличается от индивидуальных значений признака, чем во второй.
Следовательно, для всесторонней характеристики рядов распределения необходимы показатели, определяющие меру, степень колеблемости отдельных значений признака от средней, т.е. степень вариации, а также форму (тип) распределения, характеризующую ее закономерности.
7.2. Показатели вариации и способы их расчета
а) Размах вариации является наиболее простой мерой колеблемости значений признака и представляет собой разность между максимальным и минимальным значением признака: R = Хmax - Хmin.
Размах вариации имеет недостаток, проявляющийся в том, что при вычислении R используется только крайние значения ряда распределения, и он не всегда правильно характеризует колеблемость признака.
В связи с тем, что каждое индивидуальное значение признака отклоняется от средней на определенную величину, мерой вариации может служить средняя из отклонений каждой отдельной варианты от их средней.
Такими показателями являются среднее линейное отклонение, дисперсия, среднее квадратическое отклонение.
б) Среднее линейное отклонение представляет собой среднюю из абсолютных значений отклонений индивидуальных значений признаков от их средней:
 ;
;  .
.
Недостаток среднего линейного отклонения в том, что оно берется без учета знака. Поэтому в статистике чаще используют дисперсию и среднее квадратическое отклонение.
в) Дисперсия и среднее квадратическое отклонение. Дисперсией называется средний квадрат отклонений индивидуальных значений признака от их средней величины
 ;
;  .
.
Дисперсия имеет очень большое значение в анализе. Однако ее применение как меры вариации в ряде случаев бывает не совсем удобным, потому что размерность дисперсии равна квадрату размерности изучаемого признака. Поэтому вычисляют среднее квадратическое отклонение, равное корню квадратному из суммы квадратов отклонений индивидуальных значений признака от их средней, т.е. из дисперсии
 .
.
Сопоставление линейных или средних квадратических отклонений по нескольким совокупностям дает возможность определять степень их однородности в отношении того или иного признака. Чем меньше: R, d, σ2,σ, тем совокупность более однородна, тем более типичной будет средняя величина.
г) Коэффициент вариации. Так как дисперсия и среднее квадратическое отклонение характеризуют абсолютный размер отклонений, то представляет интерес сопоставить среднее квадратическое отклонение с его средней величиной. Такой показатель называется коэффициентом вариации
 .
.
Если
взять отношение среднего линейного
отклонения к средней арифметической,
то получим линейный
коэффициент вариации
 .
.
Отношение
размаха вариации к средней арифметической
называется коэффициентом осцилляции:
 .
.
Взаимосвязь показателей вариации
В
нормальном ряду распределения между
показателями вариации имеются следующие
примерные соотношения:
7.3. Основные свойства дисперсии
Если все значения признака уменьшить или увеличить на какое-то постоянное число а, то дисперсия не изменится.
Если все значения признака уменьшить или увеличить в К раз, то дисперсия изменится в К2 раз.
Сумма квадратов отклонений индивидуальных значений признака x от их средней
 меньше суммы квадратов отклонений
индивидуальных значений признака от
любого числа а,
при условии, что
меньше суммы квадратов отклонений
индивидуальных значений признака от
любого числа а,
при условии, что
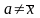
 .
.
Дисперсия признака равна разности между средним квадратом значения признака и квадратом их средней:
 .
.
Дисперсия альтернативного признака
В ряде случаев возникает необходимость измерить вариацию альтернативного признака, то есть такого, который может принимать только два значения. Обозначив отсутствие интересующего нас признака через 0, его наличие через 1, долю единиц, обладающих данным признаком через р, не обладающих — через q, дисперсию этого признака можно определить как

Например, если 64% работников предприятия имеют высшее образование р, то дисперсия будет равна:
 .
.
7.4. Правило сложения дисперсий
На вариацию признака влияют различные причины и факторы, которые делятся на случайные и систематические. Поэтому и вариация может быть случайной, вызванной действием случайных причин и систематической, обусловленной воздействием постоянных причин и факторов. В связи с этим возникает необходимость в определении случайной систематической составляющей и её роли в общей вариации. Общую дисперсию мы уже рассматривали. Она характеризует общую вариацию признака под влиянием всех условий, всех причин, вызывающих эту вариацию и исчисляется по формуле:

Для определения влияния постоянного фактора на величину вариации пользуются аналитической группировкой. Вариация, обусловленная фактором, положенным в основание группировки, называется межгрупповой вариацией. Размеры ее определяются при помощи дисперсии групповых средних или межгрупповой дисперсии, которая характеризует колеблемость групповых или частных средних около их общей средней:
 ,
,
где
 -
средняя по каждой отдельной группе;
- средняя по всей совокупности; n
- число единиц совокупности;
f
-
частоты или веса.
-
средняя по каждой отдельной группе;
- средняя по всей совокупности; n
- число единиц совокупности;
f
-
частоты или веса.
Таким образом, межгрупповая дисперсия (дисперсия групповых средних) равна средней арифметической из квадратов отклонений частных средних от общей средней. Она характеризует систематическую вариацию, которая возникает под влиянием фактора, признака, положенного в основание группировки.
Для определения влияния случайных факторов и их роли в общей вариации определяют дисперсию в пределах каждой группы, т.е. внутригрупповую дисперсию, а затем и среднюю из внутригрупповых дисперсий:
 где
x
- индивидуальные значения признака;
-
групповые или частные средние:
где
x
- индивидуальные значения признака;
-
групповые или частные средние:
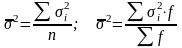
В математической статистике доказано, что общая дисперсия признака равна сумме межгрупповой дисперсии и средней из внутригрупповых дисперсий.

Это правило называется правилом сложения дисперсий.
7.5. Ряды распределения и их моделирование
а) Моменты распределения
Одной из важных задач анализов рядов распределения является выявление закономерности распределения, определение ее характера и количественного выражения. Эта задача решается при помощи показателей, характеризующих форму, тип распределения.
Кроме рассмотренных выше важной характеристикой рядов распределения являются моменты распределения.
Моментом распределения (Мк) называется средняя арифметическая из отклонений значений признака x от некоторой постоянной величины а в степени к:

Величина к определяет порядок момента. В зависимости от величины а различают начальные, центральные и условные моменты (табл. 5.2).
Таблица 7.2
Значение моментов распределения
Величина |
Название момента |
Обозначение момента |
Величина момента
|
||
|
|
|
к=0 |
к=1 |
к=2 |
0 |
начальный |
М |
1 |
|
|
|
центральный |
M |
1 |
0 |
σ |
а |
условный |
М |
|
||
Условные моменты используются для определения дисперсий высоких степеней. Практически используются моменты первых четырех порядков. Если в качестве весов взять не частоты, а вероятности, то получим теоретические моменты распределения.
б) Кривые распределения
Для обобщенной характеристики особенностей формы распределения применяются кривые распределения, которые выражают закономерность распределения единиц совокупности по величине варьирующего признака.
Эмпирическая кривая - это фактическая кривая, полученная по данным наблюдения, в которой отражаются как общие, так и случайные условия, определяющие распределение (кривая 1, рис.5.3)
Теоретическая кривая распределения - это кривая, выражающая функциональную связь между изменением варьирующего признака и изменением частот и характеризующая определенный тип распределения (кривая 2, рис.5.3).
По форме кривые распределения бывают симметричными и асимметричными. В зависимости от того, какая ветвь кривой вытянута, различают правостороннюю асимметрию и левостороннюю асимметрию (рис.5.1). Кривые распределения также могут иметь различную островершинность (рис.5.2).
Для характеристики степени асимметрии кривой используют коэффициент асимметрии, который представляет собой отношение центрального момента третьего порядка к среднему квадратическому отклонению в кубе
 .
.
Если А > 0, то асимметрия правосторонняя, а если А < 0, то асимметрия левосторонняя, в симметричном распределении А=0. Кроме этого коэффициента для характеристики асимметрии применяют и соотношение между и модой или медианой по отношению к среднеквадратическому отклонению.
 .
Он менее точен по сравнению с коэффициентом
асимметрии и применяется реже.
.
Он менее точен по сравнению с коэффициентом
асимметрии и применяется реже.
Для характеристики островершинности кривой распределения применяют коэффициент эксцесса, который равен отношению центрального момента четвертого порядка к дисперсии в квадрате
 .
.
В нормальном распределении Е=3, поэтому, если Е>3, то эксцесс выше нормального (островершинная кривая), Е<3, эксцесс ниже нормального (плосковершинная кривая).
в) Моделирование рядов распределения
Все рассмотренные выше показатели характеризуют отдельные свойства совокупности. Общую характеристику ряда распределения можно представить аналитически, в виде функции, характеризующей зависимость между изменениями признака и частотами. Если имеется эмпирический ряд распределения, то необходимо найти функцию распределения, т. е. подобрать такую теоретическую кривую, которая наиболее полно бы раскрывала закономерность распределения. Нахождение функции кривой распределения называется моделированием.
Для
аппроксимации (выравнивания) эмпирических
кривых распределения в статистике часто
пользуются нормальным распределением,
функция которого
 ,
,
где F(x) - интегральная функция распределения; t - нормированное отклонение; e - основание натуральных логарифмов.
Теоретическое распределение вероятностей и частот дает представление о форме, типе распределения, о закономерности, свойственной изучаемому явлению.
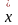 МеМо
=Ме=Мо
МеМо
МеМо
=Ме=Мо
МеМо
Правосторонняя Симметричная Левосторонняя
Асимметрия кривая асимметрия

Рис. 7.1 Типы кривых распределения (по асимметрии)
Р ис.
7.2 Типы кривых распределения (по
островершинности)
ис.
7.2 Типы кривых распределения (по
островершинности)

Эмпирическое и теоретическое распределение рабочих по степени выполнения норм приведено в табл.7.3 и на рис.7.3.
Таблица 7.3
Распределение рабочих по степени выполнения норм выработки
Группы рабочих по степени выполнения норм,% |
Число рабочих (эмпирические частоты) (f) |
Теоретические частоты (f’) |
до 100 |
2 |
5 |
100-110 |
15 |
13 |
110-120 |
26 |
24 |
120-130 |
32 |
28 |
130-140 |
12 |
20 |
140-150 |
9 |
8 |
150 и выше |
4 |
2 |
Итого: |
100 |
100 |
г) критерии согласия
Для оценки близости эмпирического и теоретического распределения используются специальные показатели, которые называются критериями согласия. Критерии согласия как правило тем или иным способом оценивают степень расхождения между эмпирическими и теоретическими частотами.
Наиболее
часто используется критерий, который
называется
хи-квадрат
Пирсона
и рассчитывается
 ,
,
где f’-теоретические частоты, f-эмпирические частоты.
Чем
меньше значение
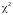 ,
тем лучше теоретическое распределение
отражает реальное положение в совокупности
и наоборот. Если
=0,
то расхождение между f
и
f’
отсутствует.
,
тем лучше теоретическое распределение
отражает реальное положение в совокупности
и наоборот. Если
=0,
то расхождение между f
и
f’
отсутствует.
Для
проверки согласия с помощью
рассчитанное значение
 сравнивают
с табличным и при условии
<
сравнивают
с табличным и при условии
<
 можно
с определенной вероятностью сказать,
что расхождение теоретического и
эмпирического распределения случайно,
и наоборот.
можно
с определенной вероятностью сказать,
что расхождение теоретического и
эмпирического распределения случайно,
и наоборот.
Также
применяется и критерий согласия
Колмогорова
 ,
который равен
,
который равен
 ,
где D
- максимальная разность накопленных
частот (без учета знака), n
- объем совокупности.
,
где D
- максимальная разность накопленных
частот (без учета знака), n
- объем совокупности.
Вычислив
фактический критерий
 ,
по специальной таблице находят вероятность
достижения критерием этого значения.
Если вероятность значительна, то
расхождение между эмпирическим и
теоретическим распределением можно
считать случайным.
,
по специальной таблице находят вероятность
достижения критерием этого значения.
Если вероятность значительна, то
расхождение между эмпирическим и
теоретическим распределением можно
считать случайным.
В явлениях общественной жизни асимметричные распределения встречаются гораздо чаще, чем симметричные. Некоторые асимметричные распределения могут быть приведены к симметричному путем преобразования признака Х, например логарифмированием. В этом случае распределение называется логарифмически нормальным. Такое преобразование производится, как правило, для сильно асимметричных распределений.
Пример 1. Проверка пряжи на крепость в лаборатории дала следующие результаты (табл. 7.4):
Таблица 7.4
Крепость пряжи, г (х) |
150 |
160 |
170 |
180 |
190 |
200 |
210 |
Количество проб, (f) |
2 |
13 |
24 |
31 |
20 |
4 |
6 |
Вычислить все показатели вариации.
Решение.
В
задаче значения признака имеют различную
численность, поэтому значения,
,
d,
 ,
,
 ,
V
должны
вычисляться как средние взвешенные
величины. Для вычисления показателей
вариации проводим дополнительные
расчеты (табл. 7.5)
,
V
должны
вычисляться как средние взвешенные
величины. Для вычисления показателей
вариации проводим дополнительные
расчеты (табл. 7.5)
Таблица 7.5
x |
f |
xf |
(x - ) |
(x - )f |
(x - )2 |
(x - )2f |
150 |
2 |
300 |
-29 |
-58 |
841 |
1682 |
160 |
13 |
2080 |
-19 |
-247 |
361 |
4693 |
170 |
24 |
4080 |
-9 |
-216 |
81 |
1944 |
180 |
31 |
5580 |
1 |
31 |
1 |
31 |
190 |
20 |
3800 |
11 |
220 |
121 |
2420 |
200 |
4 |
800 |
21 |
84 |
441 |
1764 |
210 |
6 |
1260 |
31 |
186 |
961 |
5766 |
Итого |
100 |
17900 |
|
+521 -521 |
|
18300 |
Средняя крепость пряжи определяется по формуле
 г.
г.
Размах вариации
 г.
г.
Среднее линейное отклонение вычисляется по формуле
 г.
г.
Дисперсия, взвешенная по частоте вариантов, равна
 г2.
г2.
Среднее квадратичное отклонение равно:
 г.
г.
коэффициент вариации составляет
 .
.
Пример 2. На предприятии 64% работников имеют среднее и высшее образование. Определить дисперсию доли рабочих, имеющих среднее и высшее образование.
Решение. Дисперсия альтернативного признака определяется как =pq, где p – доля единиц совокупности, обладающих данным признаком, а q=1-p – доля единиц совокупности, не обладающих данным признаком, следовательно: =0,64·0,36=0,2304.
Приме 3. Имеются следующие данные (табл.7.6):
Таблица 7.6
Заработная плата рабочих по профессиям (1997 год), тыс. руб.
№ п/п
|
Группы рабочих по профессиям |
Число рабочих |
З/п одного рабочего в месяц |
1 |
Токари |
2 |
140, 160 |
2 |
Слесари |
3 |
120, 200, 160 |
3 |
Кузнецы |
5 |
140, 180, 200, 220, 260 |
Вычислить:
среднюю месячную заработную плату для каждой группы и для всех рабочих; групповые дисперсии; среднюю из внутригрупповых дисперсий; межгрупповую дисперсию; общую дисперсию; проверить правило сложения дисперсий и сделать выводы.
Решение. В задаче требуется определить, как влияют на изменение заработной платы рабочих постоянные причины, положенные в основание группировки (в данном случае различия в профессии), и случайные причины. Для этого необходимо определить систематическую и случайную вариации и их роль в общей вариации. Для решения задачи и вычисления заданных показателей, построим вспомогательную таблицу (табл.7.7).
Таблица 7.7
№ п/п |
x |
x– |
|
|
|
Токари |
|||||
1 |
140 |
-10 |
100 |
-38 |
1444 |
2 |
160 |
10 |
100 |
-18 |
324 |
Итого: |
300 |
0 |
200 |
|
|
Слесари |
|||||
1 |
120 |
-40 |
1600 |
-58 |
3364 |
2 |
200 |
40 |
1600 |
22 |
484 |
3 |
160 |
0 |
0 |
-18 |
324 |
Итого: |
480 |
|
3200 |
|
|
Кузнецы |
|||||
1 |
140 |
-60 |
3600 |
-38 |
1444 |
2 |
180 |
-20 |
400 |
2 |
4 |
3 |
200 |
0 |
0 |
22 |
484 |
4 |
220 |
20 |
400 |
42 |
1764 |
5 |
260 |
60 |
3600 |
82 |
6724 |
Итого: |
1000 |
0 |
8000 |
|
|
Всего: |
1780 |
|
11400 |
|
16360 |
Среднюю заработную плату по каждой группе и для всех рабочих определяем по формуле средней арифметической простой:

Внутригрупповые дисперсии вычисляем по формуле:
 Средняя
из внутригрупповых дисперсий
равна:
Средняя
из внутригрупповых дисперсий
равна:

Межгрупповая дисперсия определяется как:
 ,
,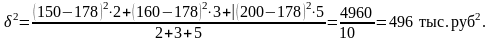
Общая
дисперсия
равна:

По
правилу сложения дисперсий общая
дисперсия равна сумме средней
внутригрупповых и межгрупповой дисперсии:
2
=
 2
+ 2
= 1140 + 496 = 1636.
2
+ 2
= 1140 + 496 = 1636.
Пример 4. Средняя успеваемость студентов экономического факультета =4 балла, Мо=4,8 балла, Ме=4,2 балла. Указать, симметричным или асимметричным является распределение студентов по успеваемости. Если асимметричным, то с какой асимметрией (левосторонней или правосторонней).
Решение. В симметричном распределении =Мо=Ме. В нашей задаче такого равенства нет. Следовательно, распределение асимметрично, а так как <Ме<Мо, то разности между –Ме и –Мо отрицательные и асимметрия левосторонняя.
Пример 5. Урожайность сахарной свеклы в сельхозпредприятиях области характеризуется следующими показателями: =300 ц/га, =120 ц/га, Мо=240 ц/га, а урожайность зерновых - =30ц/га; =10 ц/га, Мо=27 ц/га. Вычислить показатели асимметрии и указать где она больше. Каково направление асимметрии?
Решение.

Асимметрия
правосторонняя, так как
 >0,
и больше в первом случае.
>0,
и больше в первом случае.
Пример
6.
Центральный момент третьего порядка
 =34,56
при
=34,56
при
 =12.
Вычислить коэффициент асимметрии и
сделать выводы; центральный момент
четвертого порядка
=12.
Вычислить коэффициент асимметрии и
сделать выводы; центральный момент
четвертого порядка
 =64,32 при
=2
. Вычислить коэффициент эксцесса и
сделать выводы.
=64,32 при
=2
. Вычислить коэффициент эксцесса и
сделать выводы.
Решение.

Асимметрия правосторонняя, так как A>0 , и незначительная

Эксцесс выше нормального, потому что E>3.
Тема 8. Выборочное наблюдение
8.1. Общие сведения о выборочном наблюдении
В связи с тем, что статистика имеет дело с массовыми совокупностями статистические исследования весьма трудоемки. Поэтому давно возникла мысль о замене сплошного наблюдения выборочным.
Выборочное наблюдение это наиболее совершенный способ несплошного наблюдения, при котором обследуется не вся совокупность, а лишь ее часть, отобранная по определенным правилам выборки и обеспечивающая получение данных, характеризующих всю совокупность в целом.
При проведении выборочного наблюдения нельзя получить абсолютно точные данные. Как при сплошном, так как при выборочном наблюдении неизбежны ошибки, которые делятся на ошибки регистрации и ошибки репрезентативности. В свою очередь, ошибки репрезентативности бывают случайные и систематические.
Важнейшим условием применения выборочного метода является правильный отбор единиц совокупности, а именно:
а) строго объективный отбор единиц совокупности, при котором каждая из них получала бы абсолютно одинаковую возможность попасть в выборку;
б) достаточное количество отобранных единиц совокупности. При соблюдении этих условий выборка будет репрезентативной или представительной.
Вся совокупность единиц, из которой производится отбор, называется генеральной совокупностью и обозначается буквой N. Часть генеральной совокупности, попавшая в выборку, называется выборочной совокупностью и обозначается n.
Обобщающие
показатели генеральной совокупности
- средняя, дисперсная и доля - называются
генеральными
и
соответственно обозначается
 σ, р,
где
p
- доля или отношение числа единиц
совокупности М,
обладающих данным признаком ко всей
численности генеральной совокупности,
т.е.
σ, р,
где
p
- доля или отношение числа единиц
совокупности М,
обладающих данным признаком ко всей
численности генеральной совокупности,
т.е. .
Те же обобщающие характеристики в
выборочной совокупности обозначаются
соответственно
.
Те же обобщающие характеристики в
выборочной совокупности обозначаются
соответственно
 ,
,
 2,
ω.
2,
ω.
Теоретической основой выборочного метода является теорема П.Л.Чебышева, которая формулируется следующим образом: с вероятностью, сколь угодно близкой к единице (достоверности), можно утверждать, что при достаточно большом объеме выборки и ограниченной дисперсии генеральной совокупности разность между выборочной средней и генеральной средней будет сколь угодно мала:
 <
ε .
<
ε .
При практическом использовании теоремы Чебышева генеральную дисперсию , которая неизвестна, заменяют выборочной дисперсией.
8.2. Виды и схемы отбора
Формирование выборочной совокупности из генеральной может осуществляться по-разному. Различают следующие виды отбора: собственно-случайный; механический; типический; серийный; комбинированный.
Собственно-случайный отбор. Он ориентирован на выборку единиц из генеральной совокупности без всякого расчленения ее на части или группы. Либо применяется жеребьевка, либо используются таблицы случайных чисел.
Механический отбор. Он состоит в том, что отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы), причем все единицы генеральной совокупности должны располагаться в определенном порядке. Размер интервала или группы равен обратной величине доли выборки (или количеству отбираемых единиц). Из каждой группы (интервала) берется только одна единица. Так, при 2%-ной выборке отбирается каждая 50-ая единица (1:0,02; или формируется 50 групп или интервалов), при 20%-ной выборке - каждая 5-я единица (1:0,2) и т. д.
Типический отбор. При его осуществлении вся генеральная совокупность делится на группы по типическому признаку, а затем в каждой группе проводится тот или иной отбор. Наиболее часто из каждой группы выбирается количество единиц, пропорциональное удельному весу группы в общей совокупности и как правило - механическим отбором. Такой отбор часто называют пропорциональным типическим отбором с механической выборкой.
Серийный отбор с равновеликими сериями состоит в выборке не отдельных единиц генеральной совокупности, а целых серий (гнезд). Попавшие в выборку серии подвергаются сплошному наблюдению. Сами серии могут формироваться различными методами и способами.
Комбинированный отбор. Все вышеперечисленные виды отбора комбинируются между собой.
Используя различные виды отбора, можно применить и различные схемы отбора: бесповторный отбор (схема невозвращенного шара) - после выбора какой-либо единицы она обратно в генеральную совокупность не попадает и не может быть выбрана снова; повторный отбор (схема возвращенного шара) - после выбора какой-либо единицы она вновь возвращается в генеральную совокупность и может быть выбрана снова.
8.3. Определение средних и предельных ошибок при различных видах отбора
Ошибка
выборки
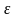
разность между характеристиками
выборочной и генеральной совокупности.
разность между характеристиками
выборочной и генеральной совокупности.
Если
 представляет собой предел, которого не
превосходит абсолютная величина
то
представляет собой предел, которого не
превосходит абсолютная величина
то

Ошибка
выборки зависит от многих факторов, и,
если из одной и той же генеральной
совокупности можно сформировать
бесконечное множество выборочных
совокупностей, каждая из них даст и свою
ошибку. Поэтому при выборочном наблюдении
говорят о средней из возможных ошибок
(средняя
или стандартная ошибка выборки), которую
обозначают как
 .
.
Величина
 прямо
пропорциональна корню квадратному из
дисперсии и обратно пропорциональна
квадратному корню из объема выборочной
совокупности;
прямо
пропорциональна корню квадратному из
дисперсии и обратно пропорциональна
квадратному корню из объема выборочной
совокупности;
 ,
для доли, соответственно
,
для доли, соответственно .
.
Эти формулы справедливы для повторной схемы отбора. При бесповторном отборе вводится поправочный коэффициент, равный
 ,
тогда
,
тогда
 .
.
В
тех случаях, когда выборка небольшая
этим множителем можно пренебречь, так
как его значение близко к единице (обычно
при
 ).
).
Для решения практических задач важна не средняя ошибка выборки, а пределы, за которые она не выйдет, т.е. говорят о предельной ошибке выборки.
Предельная
ошибка выборки связана со средней
ошибкой соотношением
 ,
где
t-
коэффициент доверия, или
t-
статистика; t
принимает значения 1, 2 или 3 и связан с
вероятностью достижения заданного
предела. Если t=1
это значит, что вероятность того, что
ошибка выборки не превысит заданного
значения, равна 0,683 или 68,3%. При t=2
P=0,954
или 95,4%;
t=3
P=0,997
или 99,7%.
,
где
t-
коэффициент доверия, или
t-
статистика; t
принимает значения 1, 2 или 3 и связан с
вероятностью достижения заданного
предела. Если t=1
это значит, что вероятность того, что
ошибка выборки не превысит заданного
значения, равна 0,683 или 68,3%. При t=2
P=0,954
или 95,4%;
t=3
P=0,997
или 99,7%.
Таким
образом, предельная ошибка выборки
зависит от трех факторов: дисперсии
 ,
объема выборки n,
и коэффициента доверия
t.
Формулы для определения предельных
ошибок при различных видах и схемах
отбора приведены в табл. 8.1.
,
объема выборки n,
и коэффициента доверия
t.
Формулы для определения предельных
ошибок при различных видах и схемах
отбора приведены в табл. 8.1.
Таблица 8.1
Определение предельной ошибки выборки при различных видах отбора
|
Схема отбора |
Предельная ошибка выборки |
|||
|
для средней
|
для доли
|
|
||
Собственно - случайный и механический отбор |
|
||||
Повторный отбор
|
|
|
|
||
Бесповторный отбор
|
|
|
|
||
Типический отбор |
|
||||
Поторный отбор |
|
|
|
||
Бесповторный отбор |
|
|
|
||
Серийный отбор |
|
||||
Повторный отбор |
|
|
|
||
Бесповторный отбор |
|
|
|
||
8.4. Определение необходимой численности выборки
При
разработке выборочного наблюдения
предполагают заранее заданными величину
допустимой ошибки выборки и вероятность
ответа (и t).
Неизвестным, следовательно, остается
тот минимальный объем выборки, который
должен обеспечить требуемую точность.
Из формулы
 и формул предельных ошибок выборки
устанавливаем необходимую численность
выборки. Формулы для определения
численности выборки n
зависят от способа отбора (табл.8.2).
и формул предельных ошибок выборки
устанавливаем необходимую численность
выборки. Формулы для определения
численности выборки n
зависят от способа отбора (табл.8.2).
Таблица 8.2
Формулы расчета численности выборки при собственно-случайном отборе
Способ отбора
|
Для средней |
Для доли |
Для доли, если даже приблизительно она неизвестна |
Повторный |
|
|
|
Бесповторный |
|
|
|
Численность
выборки можно выразить через отношение
 , т.е. предельную ошибку выборки выражают
в единицах среднего квадратичного
отклонения. Так, например, формула
численности бесповторной собственно-случайной
выборки для средней при t=3
примет вид
, т.е. предельную ошибку выборки выражают
в единицах среднего квадратичного
отклонения. Так, например, формула
численности бесповторной собственно-случайной
выборки для средней при t=3
примет вид
 .
.
Для типического и серийного отбора объем выборки определяется по специальным формулам.
Пример 1. Методом случайной повторной выборки было взято для проверки на вес 200 шт. деталей. В результате был установлен средний вес детали - 30 г при среднеквадратическом отклонении равном 4 г. С вероятностью 0,954 требуется определить предел, в котором находится средний вес детали в генеральной совокупности.
Решение.
Предельная ошибка средней при собственно-случайном отборе (повторная выборка) определится по формуле
.
Нам
известно, что t=2
(т.к. P=0.954);
 ;
n=200,
тогда
;
n=200,
тогда
 .
.
Следовательно, с вероятностью 0,954 можно утверждать, что средний вес детали в генеральной совокупности будет находиться в пределах
 .
.
Пример 2. Был проведен учет городского населения города А методом случайного бесповторного отбора. Из общей численности населения 500 тыс. человек было отобрано 500 тыс. и установлено, что 15% имеют возраст старше 60 лет. С вероятностью 0,683 определить предел, в котором находится доля жителей города А в возрасте старше 60 лет.
Решение.
Предельная ошибка доли при собственно-случайном бесповторном отборе определится как
.
Здесь
 =0.15;
1-
=
=0.15;
1-
= ;
n=50;
N=500;
t=1
(P=0.683),
тогда подставляя эти данные в формулу
получим:
;
n=50;
N=500;
t=1
(P=0.683),
тогда подставляя эти данные в формулу
получим:

Следовательно, с вероятностью 0,683 можно утверждать, что доля жителей старше 60 лет находится в пределах:
0,15-0,048<P<0,15+0,048; или 10,2%<P<19,8%.
Пример 3. Проведена 10%-ная типическая выборка пропорциональна численности отобранных групп (табл. 6.3).
Таблица 6.3
Группировка рабочих разных профессий по степени выполнения
норм выработки
Группы рабочих |
Число рабочих |
Среднее выполнение норм, % |
|
Токари |
40 |
98 |
2 |
Слесари |
60 |
108 |
3 |
Фрезеровщики |
50 |
104 |
5 |
Требуется с вероятностью 0,954 определить пределы, в которых находится средний процент выполнения норм рабочими завода в целом. Выборка бесповторная.
Решение: Вычислим общий средний процент выполнения норм выработки:
 .
.
Далее определим среднюю из групповых дисперсий
 .
.
Рассчитаем предельную ошибку выработки для типического отбора
 .
( N=1500,
т.к. выборка 10%-ная).
.
( N=1500,
т.к. выборка 10%-ная).
Таким образом, с вероятностью 0,954 можно утверждать, что средний процент выполнения норм рабочими завода в целом находится в пределах
 или
или

т.е. он не меньше 103,82% и не больше 104,18%.
Пример 4. Для определения средней урожайности сахарной свеклы в области проведена 20%-ная серийная бесповторная выборка, в которую вошло 5 районов из 25. Средняя урожайность по каждому отобранному району составила: 250, 260, 275, 280, 300 ц/га. Определить с вероятностью 0,954 пределы, в которых будет находиться средняя урожайность сахарной свеклы по области.
Решение. Найдем общую среднюю
 ц/га.
ц/га.
Определим межсерийную дисперсию по формуле
 ц/га.
ц/га.
Рассчитаем предельную ошибку выборки при серийном бесповторном отборе
 ц/га.
ц/га.
Следовательно, с вероятностью 0,954 можно утверждать, что средняя урожайность сахарной свеклы в области будет находиться в пределах от 272,66 до 287,34 ц/га.
Пример 5. Предполагается, что партия деталей содержит 8 % брака. Определить необходимый объем выборки, чтобы с вероятностью 0,954 можно было установить долю брака с погрешностью не более 2% . Исследуемая партия содержит 5000 деталей.
Решение.
По условию задачи t=2
, доля бракованных деталей
 =0,08,
=0,08,
1-
=0,92.
Предельная ошибка доли по условию равна
 =0,02,
а N=5000.
Подставляем эти данные в формулу и
получим
=0,02,
а N=5000.
Подставляем эти данные в формулу и
получим
 .
.
Чтобы с вероятностью 0,954 можно было утверждать, что предельная ошибка доли брака не превысит 2% , необходимо из 5000 деталей отобрать 642.
Пример 6. Что произойдет с предельной ошибкой выборки, если:
а) дисперсия уменьшится в 4 раза;
б) численность выборки увеличить в 9 раз;
в) вероятность исчисления изменится с 0,683 до 0,997.
Решение.
Из формулы для расчета предельной ошибки
выборки

видно, что она:
а) прямо пропорциональна корню квадратному из дисперсии. Следовательно, если дисперсия уменьшится в 4 раза, то предельная ошибка уменьшится в 2 раза;
б) обратно пропорциональна корню квадратному из численности выборки. Следовательно, если объем выборки увеличится в 9 раз, то предельная ошибка уменьшится в 3 раза;
в) прямо пропорциональна вероятности исчисления, т.е. при увеличении Р с 0,683 (t=1) до 0,997 (t=3) ошибка увеличится в 3 раза.
Тема 9. Индексы
Индекс – это относительный показатель, характеризующий изменение величины какого-либо социально-экономического явления во времени или соотношение её в пространстве.
Различают индивидуальные индексы и общие. Первые устанавливают изменение единичных, простых показателей (производства отдельного вида изделий, цен на отдельные виды продукции и т.п.), их обозначают буквой “і”. Общие индексы характеризуют изменение показателя по сложной совокупности (объема реализации продукции нескольких видов, цен на все виды проданных товаров и т.п.), их обозначают буквой “І” (рис.9.1)
Все анализируемые с помощью индексов показатели также имеют свою символику и условно делятся на три группы: количественные, качественные и объемные (некоторые из них приведены в табл.9.1.).
Таблица 9.1
Группировка статистических показателей и их символы
в индексном анализе
С т а т и с т и ч е с к и е п о к а з а т е л и |
||||||
количественные |
качественные (показатели уровня) |
объёмные |
||||
символ |
название |
символ |
название |
символ |
название |
|
q |
количество продукции |
p |
цена |
C |
выручка, товарооборот |
|
q |
количество продукции |
z |
себестоимость |
Z |
общие затраты на производство |
|
h |
посевная площадь |
u |
урожайность |
V |
валовой сбор |
|
T |
затраты труда |
w |
выработка |
q |
количество продукции |
|
T |
затраты труда |
f |
средняя зарплата |
F |
фонд заработной платы |
|
q |
количество продукции |
t |
трудоемкость |
T |
затраты труда |
|
ОФ |
стоимость ос-новных фондов |
f0 |
фондоотдача |
q |
количество продукции |
|
|
средние товарные запасы |
с |
скорость товарооборота |
ТО |
товарооборот |
|
И
н д е к с ы


По
характеру сравниваемых
совокупностей
территориальные

временные

индивидуальные
По
сложности охватываемых явлений
общие
сводные
однофакторные

По
количеству учитываемых факторов
двухфакторные

многофакторные
цепные
По
принятой базе
сравнения

базисные
агрегатные
По
способу исчисления
средних
величин

средние
их индивидуальных

средние
гармонические
средние
арифметические

Рис.9.1. Классификация индексов.
Всякий объёмный показатель есть произведение количественного на качественный, т.е. всегда C = q · p; Z = q · z; q = T · w; T =q · t и т.д. Качественными называют показатели, характеризующие уровень явления, т.е. величину объёмного показателя, приходящуюся на единицу количественного. При расчете индексов сравниваемая величина показателя (числитель отношения) называется текущей или отчетной и помечается в формулах подстрочным знаком “1”. А значение показателя, с которым ведется сравнение (знаменатель дроби), называют базисным и помечают в формулах подстрочным знаком “0”. Подстрочным знаком после символа индекса указывается символ индексируемой величины (табл. 8.1).
Индивидуальные индексы. Индивидуальные индексы представляют собой относительные величины динамики, выполнения плана, сравнения. Их расчет не требует знания специальных правил.
Формула индивидуального индекса некоторого показателя (х) записывается в следующей последовательности:
 .
.
Тогда
индивидуальные индексы отдельных
показателей имеют вид: цен -
 =
= ;
себестоимости -
;
себестоимости -
 ;
валового сбора -
;
валового сбора -
 ;
трудоемкости -
;
трудоемкости -
 ;
количества проданной продукции отдельного
вида –
;
количества проданной продукции отдельного
вида –
 и т. д.
и т. д.
Агрегатные индексы. Агрегат – сложный экономический показатель, получаемый путем произведения непосредственно не суммируемых взаимосвязанных величин с последующим суммированием результатов умножения. Такие расчеты выражают аддитивно-муль-типликативную зависимость. Агрегатные индексы являются общими.
Общие
индексы объёмных
показателей
строятся аналогично индивидуальным
индексам. Последовательность записи
формулы об-щего индекса некоторого
объёмного показателя (M)
можно представить следующим образом: .
.
Тогда, например, формулы общих индексов отдельных объёмных показателей записываются в следующем виде:
индекс
стоимости:
 или
или
 , т.к.
, т.к.
 ;
;
индекс
общих затрат:
 или
или
 ,
т.к.
,
т.к.
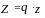 ;
;
индекс
валового сбора:
 или
или
 ,
т.к. V
= h
· u
.
,
т.к. V
= h
· u
.
Построение общих индексов количественных показателей, суммируемых в натуральном выражении, осуществляется аналогично агрегатным индексам объемных показателей, а именно: суммируются отдельные значения показателя в каждом из сравниваемых периодов и полученные суммы соотносятся между собой. Например:
индекс
затрат труда: ;
индекс посевных площадей:
;
индекс посевных площадей: .
.
При построении общих индексов количественных показателей, непосредственно несуммируемых в натуральном выражении, необходимо предварительно привести их к сопоставимому виду. Это достигается чаще всего путем выражения показателя в денежном измерении (через цену - “р” или себестоимость - “z”). Качественные показатели-соизмерители (веса) не должны влиять на динамику анализируемого количественного показателя и их следует взять неизменными, т.е. на уровне одного периода (как правило базисного) и в числителе, и в знаменателе индекса.
Формула общего индекса физического объёма и последовательность её построения следующая:

При
построении агрегатных индексов
качественных
показателей
также возникает проблема соизмерения
(взвешивания), т.к. суммирование отдельных
значений качественных показателей
(показателей уровня) лишено смысла.
Показателями-соизмерителями (весами)
при этом выступают только те количественные,
на единицу которых рассчитаны индексируемые
качественные показатели. Количественные
показатели-веса принято фиксировать
на уровне отчетного периода.
Последовательность записи формулы,
например, общего
индекса цен
будет следующей:
Агрегатные
индексы других качественных показателей
имеют вид: выработки (производительности
труда) - ;
урожайности -
;
урожайности - ; трудоемкости -
; трудоемкости - и т. д.
и т. д.
Разность между числителем и знаменателем соответствующих агрегатных индексов позволяет установить абсолютную величину изменения объемного показателя в целом, а также под влиянием отдельно количественного и качественного показателей-факторов. Знак полученной разности укажет на направление изменений: рост (+) или снижение (–).
Например, общее абсолютное изменение стоимости продукции (объемного показателя) находится как разность числителя и знаменателя агрегатного индекса стоимости:

 -
-
 (напомним, что
(напомним, что
 ).
).
Абсолютный прирост стоимости товаров за счет изменения их количества (физического объема) будет равен:

 -
-
 (напомним, что
(напомним, что
 ).
).
Абсолютный прирост стоимости товаров за счет изменения их цен:

 -
(напомним, что
-
(напомним, что
 ).
).
Таким образом, агрегатные индексы количественных и качественных показателей выступают аналитическими индексами, т.е. измерителями роли показателей-факторов в общей динамике объёмного показателя. Это требует их взаимосвязи.
Индексы
показателей связаны точно также, как
связаны сами показатели, т.е. если C
= q · p,
то и
 ;
если Z
= q · z,
то и
;
если Z
= q · z,
то и
 ;
если T
= q · t ,
то и
;
если T
= q · t ,
то и
 и т.д.
и т.д.
Покажем
эту взаимосвязь на примере индексов
стоимости, физического объема и цен:
 =
=


 =
=
 .
.
Средние из индивидуальных индексов. Средние из индивидуальных индексов образуются из агрегатной формы индекса, когда нет данных об абсолютных значениях индексируемой величины за базис-ный и отчетный периоды, но известно относительное её изменение в динамике (индивидуальный индекс). При этом из формулы индиви-дуального индекса выводят недостающую для агрегатного индекса величину и полученное выражение подставляют в исходную формулу.
Так,
агрегатный индекс физического объема
(
)
преобразовы-вается в средний арифметический
индекс, когда из формулы индивидуального
индекса физического объема ( )
выводят величину числителя:
)
выводят величину числителя: и
полученное выражение подставляют в
числитель агрегатного индекса
и
полученное выражение подставляют в
числитель агрегатного индекса
 ;
агрегатный индекс цен (
;
агрегатный индекс цен ( )
преобразовыва-ется в средний гармонический
индекс, когда из формулы индивидуального
индекса цены (
)
преобразовыва-ется в средний гармонический
индекс, когда из формулы индивидуального
индекса цены ( )
находится знаменатель:
)
находится знаменатель:
 и полученное выражение подставляется
в знаменатель агрегатного индекса цен
-
и полученное выражение подставляется
в знаменатель агрегатного индекса цен
-
 .
.
Индексы
средних величин. Из
трех видов показателей, выделяемых в
индексном анализе, осредняют индивидуальные
значения только качественных. Расчет
их средних уровней ведут по формуле
средней арифметической взвешенной ( ).
Например:
).
Например:
-
средняя
цена
некоторого товара “А”, продаваемого
несколькими торговыми предприятиями,
будет равна:

где p - цена товара “А” на каждом торговом предприятии; q - количество товара “А”, проданного каждым торговым предприятием;
- средняя себестоимость некоторого изделия “С”, производимого несколькими предприятиями:
 ,
,
где z - уровень себестоимости изделия “С” на каждом предприятии, q - количество изделий данного вида, произведенного каждым предприятием.
Относительная оценка изменения во времени среднего уровня качественного показателя ведется с помощью индекса переменного состава, который, например, для средней цены имеет вид:
 :
: =
= .
.
Разность числителя и знаменателя этого индекса устанавливает абсолютное изменение анализируемого показателя
 .
.
Чтобы установить, как изменилась величина среднего показателя за счет изменения только индивидуальных значений осредняемого признака (в нашем примере - индивидуальных цен), рассчитывают индекс постоянного (фиксированного) состава. Применительно к показателю средней цены он имеет вид:
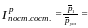
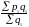 :
: =
= .
.
Если
найти разность числителя и знаменателя
индекса фиксированного состава, будет
получено абсолютное изменение средней
цены за счет изменений в отчетном периоде
по сравнению с базисным индивидуальных
цен товара, продаваемого разными
объектами:

Влияние изменений в структуре совокупности на динамику среднего показателя устанавливают с помощью индекса структурных сдвигов. Покажем его вид на примере средней цены:

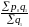 :
:
 =
= .
.
Чтобы установить на сколько изменилась средняя цена товара в результате изменения в структуре ее реализации нужно вычислить разность числителя и знаменателя индекса структурных сдвигов.
 .
.
Прикладные
индексные модели. Рассмотренные
принципы построения индексов не являются
единственно возможными в
экономико-статистическом анализе. Так,
агрегатный индекс цен с весами,
зафиксированными на уровне отчетного
периода ( ),
называется индексом Пааше и используется,
как было отмечено, в оценке динамики
розничных цен. Несколько иной результат
будет получен, если применить веса
базисного периода:
),
называется индексом Пааше и используется,
как было отмечено, в оценке динамики
розничных цен. Несколько иной результат
будет получен, если применить веса
базисного периода: .
Этот индекс служит основой для расчета
индекса потребительских цен и называется
формулой Ласпейреса. Он позволяет
установить изменение потребительских
расходов в текущем периоде по сравнению
с базисным, если при изменении цен
уровень и структура потребления останутся
прежними. Поэтому значение данного
индекса в оценке динамики цен возрастает
в условиях высоких темпов инфляции,
когда как раз не происходит существенных
изменений ни в объеме, ни в структуре
потребления.
.
Этот индекс служит основой для расчета
индекса потребительских цен и называется
формулой Ласпейреса. Он позволяет
установить изменение потребительских
расходов в текущем периоде по сравнению
с базисным, если при изменении цен
уровень и структура потребления останутся
прежними. Поэтому значение данного
индекса в оценке динамики цен возрастает
в условиях высоких темпов инфляции,
когда как раз не происходит существенных
изменений ни в объеме, ни в структуре
потребления.
Средняя
геометрическая из индексов Пааше и
Ласпейреса получила название “индекс
Фишера”: Данная формула применяется в случаях
трудностей с выбором весов или
значительного изменения структуры
весов.
Данная формула применяется в случаях
трудностей с выбором весов или
значительного изменения структуры
весов.
В
статистической теории известен индекс
цен, получивший название формулы
Эджворта-Маршалла:
 .
.
Многие сложные экономические явления описываются смешанной (аддитивно-мультипликативной) функциональной зависимостью. Так, например, среднюю производительность труда одного работника (W) можно представить произведением четырех показателей-факто-ров: средней часовой производительности труда (wчас), средней продолжительности рабочего дня (tчас), средней продолжительности рабочего периода (tдн), долей рабочих в общей численности работников предприятия (dр). Общий вид модели будет таким: W = wчас· tчас· tдн · dр
Для установления влияния каждого показателя-фактора (сомножителя) на результативный показатель-функцию (W) в индексном анализе используются два подхода:1) схема обособленного учета влияния факторов; 2) последовательно-цепная схема разложения.
Каждый из них имеет свои достоинства и недостатки. Покажем их, обозначив показатели-факторы буквами: “а”, “в”, “с”, “d”, а результативный показатель-функцию буквой “У”.
При определении влияния каждого фактора методом их обособленного учета любой частный индекс (субиндекс) строят в предположении, что изменяется от базисного периода к отчетному уровень только данного фактора, величины же всех остальных показателей остаются неизменными, зафиксированными на уровне базисного периода. При данной схеме не имеет значения очередность рассмотрения факторов (это достоинство метода), т.к. при любой очередности получают одинаковые результаты. Но произведение частных индексов не дает полной взаимосвязи с общим индексов (в этом состоит недостаток метода):
 ≠
≠



 .
.
 При
определении влияния факторов
последовательно-цепным методом (с
помощью взаимосвязанных частных
индексов) предполагают, что факторы
оказывают свое влияние на изменение
экономического явления в определенной
последовательности, при этом каж-
дый
следующий фактор действует при условии
уже изменившихся ранее учтенных факторов.
Достоинство и недостаток первого метода
меняются местами, а именно: произведение
частных индексов дает общий индекс, но
возникает вопрос о том, в какой
последовательности должны быть
расположены и рассмотрены факторы. От
этого зависит размер изменения явления,
приписываемый каждому из них. Другими
словами, в первую очередь необходимо
решить, какой из двух очередностей
отдать предпочтение: a
в с d
При
определении влияния факторов
последовательно-цепным методом (с
помощью взаимосвязанных частных
индексов) предполагают, что факторы
оказывают свое влияние на изменение
экономического явления в определенной
последовательности, при этом каж-
дый
следующий фактор действует при условии
уже изменившихся ранее учтенных факторов.
Достоинство и недостаток первого метода
меняются местами, а именно: произведение
частных индексов дает общий индекс, но
возникает вопрос о том, в какой
последовательности должны быть
расположены и рассмотрены факторы. От
этого зависит размер изменения явления,
приписываемый каждому из них. Другими
словами, в первую очередь необходимо
решить, какой из двух очередностей
отдать предпочтение: a
в с d
 =
=



или d c b a:
 =
=


 .
.
В решении этой проблемы исходят из общепринятого правила взвешивания при построении индексов: веса – качественные показатели берутся базисными, а веса – количественные показатели следует фиксировать на уровне отчетного периода. В соответствии с этим требованием, в первую очередь, необходимо учитывать влияние количественных показателей-факторов, а очередность расположения всех факторов должна быть такой, чтобы еще не рассмотренные факторы в произведении давали качественный показатель. Это положение в нашем случае требует очередности: d c b a:
Примирить оба подхода возможно с помощью приема, который получил название цепных показателей. Относительное влияние каждого фактора на общую динамику результативного показателя устанавливается при этом через соотношение соответствующих индексов: в числителе дроби берется разность индексов числителя и знаменателя расчетной формулы показателя-фактора, а в знаменателе – индекс знаменателя расчетной формулы показателя-функции. Для нахождения абсолютного изменения показателя-функции за счет каждого фактора достаточно каждый цепной относительный показатель умножить на уровень результативного показателя-функции в базисном периоде.
Пример 1. Имеются следующие данные о производстве продукции на заводе:
Вид из-делия |
Объем производства, тыс.шт |
Себестоимость, тыс.руб./шт |
|||
базисный период |
отчетный период |
базисный период |
отчетный период |
||
А |
2,5 |
3,0 |
20 |
18 |
|
Б |
1,4 |
1,75 |
30 |
36 |
|
Вычислите: 1) индивидуальные индексы себестоимости, физического объема производства и затрат на производство продукции А; 2) общий индекс затрат; 3) общий индекс физического объема производства продукции; 4) общий индекс себестоимости; 5) общее абсолютное изменение затрат на производство продукции, в том числе за счет изменения количества и себестоимости продукции. Покажите взаимосвязь между исчисленными индексами.
Решение
Индивидуальные индексы рассчитаем для изделия “А”:
а)
себестоимости
 ;
;
 или 90%, т.е. себестоимость изделия А
снизилась на 10%.
или 90%, т.е. себестоимость изделия А
снизилась на 10%.
б)
количества произведенной продукции:
 ;
;
 или
120%, т.е. объем производства этого изделия
вырос на 20%.
или
120%, т.е. объем производства этого изделия
вырос на 20%.
в)
затрат
на производство продукции: ;
; или 108%, т.е. затраты на производство
продукции А выросли на 8%.
или 108%, т.е. затраты на производство
продукции А выросли на 8%.
Общий (агрегатный) индекс затрат определяется по формуле:

 или
127,2 %, т.е. затраты на производство в
отчетном периоде по сравнению с базисным
увеличились на 27,2 %.
или
127,2 %, т.е. затраты на производство в
отчетном периоде по сравнению с базисным
увеличились на 27,2 %.
Общий (агрегатный) индекс физического объема производст-ва продукции равен:

 или
122,3 % т.е. общий объем производства
продукции вырос на 22,3 %.
или
122,3 % т.е. общий объем производства
продукции вырос на 22,3 %.Общий (агрегатный) индекс себестоимости равен:

 или
104 %, т.е. себестоимость всей разнородной
продукции выросла в среднем на 4 %.
или
104 %, т.е. себестоимость всей разнородной
продукции выросла в среднем на 4 %.
5.
Общее абсолютное изменение затрат на
производство продукции в отчетном
периоде по сравнению с базисным
определяется по данным общего индекса
затрат и равно разности между числителем
и знаменателем этого индекса: 117-92=25
тыс. руб.
117-92=25
тыс. руб.
Абсолютное
изменение затрат на производство
продукции за счет изменения объема
производства определяется по данным
общего индекса физического объема
производства и равно разности между
числителем и знаменателем этого индекса:
 112,5
– 92 = 20,5 тыс. руб.
112,5
– 92 = 20,5 тыс. руб.
Абсолютное
изменение затрат на производство
продукции за счет изменения себестоимости
изделий определяется по данным общего
индекса себестоимости и равно разности
между числителем и знаменателем этого
индекса: 117-112,5=4,5
тыс. руб.
117-112,5=4,5
тыс. руб.
Таким образом, в отчетном периоде по сравнению с базисным затраты на производство продукции выросли на 27,2 % или на 25 тыс. грн. Объем производства продукции вырос на 22,3 % и за счет этого затраты на производство продукции выросли на 20,5 тыс. руб.
Себестоимость
продукции выросла на 4 %, и это привело
к увеличению затрат на 4,5 млн. руб. Между
исчисленными индексами существует
взаимосвязь
 =1,223 · 1,040 = 1,272.
=1,223 · 1,040 = 1,272.
Пример 2. По имеющимся данным о производстве продукции на заводе вычислите: 1) общий индекс физического объема производства продукции; 2) как изменилась стоимость произведенной продукции под влиянием изменения количества произведенных изделий.
Вид изделия |
Произведено в прошлом году, тыс. руб |
Индекс количества произведенной продукции в текущем году по сравнению с прошлым годом |
Пылесосы Электроутюги |
200 150 |
0,95 1,20 |
Итого |
350 |
- |
Решение
1. Для определения относительного изменения объема производства продукции в текущем году по сравнению с прошлым годом следует использовать средний арифметический индекс:

 или
105,7 %
или
105,7 %
Следовательно, объем производства двух видов продукции по заводу вырос на 5,7 %.
2.
 =370-350
= +20 тыс. руб.; т.е. рост физического объема
производства привел к увеличению
стоимости произведенной продукции в
текущем году на 20 тыс. руб.
=370-350
= +20 тыс. руб.; т.е. рост физического объема
производства привел к увеличению
стоимости произведенной продукции в
текущем году на 20 тыс. руб.
Пример 3. Имеются следующие данные о продаже товаров по центральному универмагу города:
Товарные группы |
Товарооборот ΙΙ квартала, тыс. руб |
Увеличение (+), уменьшение (-) цены во ΙΙ квартале по сравнению с I кварталом, % |
Ткани |
61,5 |
+105 |
Галантерея |
16,5 |
-3 |
Вычислите: 1) общий индекс цен; 2) сумму экономии или пер-расхода, вызванную изменением цен.
Решение
Общий индекс цен равен:
 .
Для вычисления этого индекса определим
предварительно индивидуальные индексы
цен:
.
Для вычисления этого индекса определим
предварительно индивидуальные индексы
цен:
для тканей: iР = 100 + 105 = 205% или 2,05;
для галантереи: iР = 100 – 3 = 97% или 0,97.
Тогда: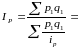
 или
166%, т.е. цены на товары во ΙΙ квартале по
сравнению с Ι кварталом выросли на 66%.
или
166%, т.е. цены на товары во ΙΙ квартале по
сравнению с Ι кварталом выросли на 66%.
Перерасход, вызванный изменением цен, составил:
 78
– 47 = 31 тыс. руб.
78
– 47 = 31 тыс. руб.
Пример 4. Имеются следующие данные о продаже товаров в универсаме № 1:
Товары |
Товарооборот в действующих ценах, тыс. руб |
Изменение цен во ΙΙ квартале по сравнению с I,% |
|
I квартал |
ΙΙ квартал |
||
Колбасные изделия |
40 |
35 |
+25 |
Рыба и рыбные продукты |
30 |
51 |
-7 |
Вычислите: 1) общий индекс товарооборота, 2) общий индекс цен; 3) общий индекс физического объема товарооборота; 4) экономию или дополнительные расходы населения, вызванные изменением цен.
Решение
Общий индекс товарооборота равен:

 = 1,229 или 122,9%, т.е. товарооборот во ΙΙ
квартале по сравнению с I кварталом
возрос на 22,9% или на 16 тыс. руб. (86 – 70).
= 1,229 или 122,9%, т.е. товарооборот во ΙΙ
квартале по сравнению с I кварталом
возрос на 22,9% или на 16 тыс. руб. (86 – 70).Общий индекс цен определяем по формуле:
 .
.
Индивидуальные индексы цен равны:
по колбасным изделиям: iР = 100 + 25 = 125 % ,
по рыбе и рыбным продуктам: iР = 100 – 7 = 93 %.
Тогда или
103,8%, т.е. цены на то-вары выросли на 3,8%,
что привело к росту товарооборота на
3,16 тыс. руб. (86 - 82,84).
или
103,8%, т.е. цены на то-вары выросли на 3,8%,
что привело к росту товарооборота на
3,16 тыс. руб. (86 - 82,84).
3.
Общий индекс физического объема
товарооборота определим исходя из
взаимосвязи индексов: =1,229
: 1,038 = 1,184 или 118,4%, т.е. физический объем
продажи товаров вырос на 18,4%.
=1,229
: 1,038 = 1,184 или 118,4%, т.е. физический объем
продажи товаров вырос на 18,4%.
4.
Дополнительные расходы населения,
вызванные ростом цен на товары составили: =
86,0 - 82,84 = 3,16 тыс. руб., т.е. они равны
исчисленному выше приросту товарооборота
за счет роста цен.
=
86,0 - 82,84 = 3,16 тыс. руб., т.е. они равны
исчисленному выше приросту товарооборота
за счет роста цен.
Пример 5. Имеются следующие данные о продаже картофеля на двух рынках города:
Номер рынка |
Базисный период |
Отчетный период |
|||
продано, тыс.кг |
цена за 1кг, руб. |
продано,тыс.кг |
цена за 1кг,руб. |
||
1 |
1200 |
1,30 |
600 |
1,35 |
|
2 |
800 |
1,40 |
900 |
1,32 |
|
Вычислите: 1) индекс средней цены переменного состава; 2) ин-декс средней цены постоянного состава; 3) индекс средней цены структурных сдвигов; 4) абсолютное изменение средней цены картофеля всего, в том числе за счет изменения: а) цены на каждом рынке; б) структуры продажи картофеля; 5) абсолютное изменение товарооборота, вызванное изменением объема, структуры продажи и цен на картофель.
Решение
Индекс цены переменного состава равен:


 :
:
= 0,985 или 98,5%. Средняя цена картофеля в отчетном периоде по сравнению с базисным снизилась на 1,5%.
Это снижение вызвано изменением цены картофеля и структуры его продажи по рынкам.
Индекс цены постоянного состава равен:


 0,971
или 9,71%. Средняя цена картофеля за счет
изменения цен на рынке снизилась на
2,9%.
0,971
или 9,71%. Средняя цена картофеля за счет
изменения цен на рынке снизилась на
2,9%.
Индекс цены структурных сдвигов:


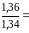 1,015
или 101,5%, т.е. изменение структуры продажи
картофеля по рынкам привело к росту
средней цены картофеля на 1,5%.
1,015
или 101,5%, т.е. изменение структуры продажи
картофеля по рынкам привело к росту
средней цены картофеля на 1,5%.
В отчетном периоде по сравнению с базисным средняя цена картофеля снизилась на:
 1,32
– 1,34 = = - 0,02 руб., в том числе за счет
изменения:
1,32
– 1,34 = = - 0,02 руб., в том числе за счет
изменения:
а)
цены на картофель по рынкам:
 =
1,32 – 1,36 = - 0,04 руб.;
=
1,32 – 1,36 = - 0,04 руб.;
б)
структуры продажи картофеля: =
1,36 – 1,34 = 0,02 руб.
=
1,36 – 1,34 = 0,02 руб.
Абсолютное изменение товарооборота определяется так:
а) за счет изменения объема продажи картофеля:
 =
(1500-2000) · 1,34 = - 670 тыс. руб;
=
(1500-2000) · 1,34 = - 670 тыс. руб;
б) за счет изменения структуры продажи картофеля:
 =
2040 - 1,34 · 1500 = 30 тыс. руб. или
=
2040 - 1,34 · 1500 = 30 тыс. руб. или
 =
+ 0,02 · 1500 = 30 тыс. руб;
=
+ 0,02 · 1500 = 30 тыс. руб;
в) за счет изменения цены картофеля по рынкам:
 =
1980 – 2040 = - 60 тыс. руб. или
=
1980 – 2040 = - 60 тыс. руб. или
 =
- 0 ,04 · 1500 = - 60 тыс. руб.
=
- 0 ,04 · 1500 = - 60 тыс. руб.
Таким
образом, =
= +
+
 +
+
 =
-670 + 30 + (-60) =
=
-670 + 30 + (-60) =
= -700 тыс. руб.
1 По материалам сайта Росстата: http://www.gks.ru

 А
=
12,5
А
=
12,5 А)
/ i
=
А)
/ i
=
 12,5)
/ 5
12,5)
/ 5






 или
или

 или
или