Solving Genetics Problems I: Monohybrid Crosses

Classical genetics is a science of logic and statistics. While many find the latter intimidating, the mathematical side of most classical genetics puzzles is relatively simple — and there are actually ways to get around most of the math. The logic part is inescapable. All genetics problems are solved using the same basic logic structure. If you learn the sense of the approach, you can solve virtually any genetics problem, provided you are given enough basic information.

Let's first consider the little puzzle you were given in the "Five Rules" essay. The problem involved two gerbils named Honey and Ritz. The gene in question was a fur color gene which has two alleles — dominant brown (B) andrecessive black (b). It's a very good idea to write down the information you are given in a problem so that it will be easy for you to refer to it when necessary. So begin by writing something like this at the top of your work page:

Using the Five Rules for Pedigree Analysis, we figured out that each of our parent gerbils was heterozygous for this gene. So here is our mating:

Step One: Figure out the genotypes of the parents.

Once you've got that settled, you need to address the question of all of the possible kinds of babies they could produce. Before any parent makes babies, of course, that parent makes gametes. So in order to find what kinds of babies they can have, you must first determine what kinds of gametes they can produce. Since Honey is a heterozygote (and paying attention to Rule #1), she can produce two kinds of eggs: B eggs and b eggs. Ritz is also a heterozygote, so he can produce two kinds of sperm: B sperm and b sperm. Something like this:

Step Two: Figure out what kinds of gametes the parents can produce.

Now you need to determine all the possible ways that his sperm can combine with her eggs. There are several different techniques used for this operation. The most popular among students is the Punnett Square. Punnett Squares are probability tables — a way to do statistics while avoiding as much math as possible.

Step Three: Set up a Punnett Square for your mating.

Setting up a Punnett Square is easy. You need to create a chart with one column for each of the female's egg types, and one row for each of the male's sperm types. For Honey and Ritz, your table would look like this:

The little boxes on the inside of the table are the kinds of offspring this pair can produce. Note that, since Honey's two kinds of eggs will be produced in equal proportions, and Ritz's two sperm types will also be produced in equal proportions, each of the boxes inside should represent an equal proportion of potential offspring. A statistician would say that each of the offspring types has an equal probability.

Now we fill in the inside of the table. The upper left square represents those babies that get a B from both egg and sperm; the upper right box represents babies that get B from the sperm and b from the egg. You can figure out the rest.

Step Four: Fill in the babies inside the table by matching the egg allele at the top of the column with the sperm allele at the head of the row.

When you are finished, your completed square should look like this:

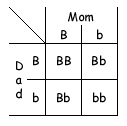
So we have now figured out that, if Honey and Ritz have a lot of babies, we can predict that 1/4 of them should be BB, 1/2 of them (2/4) should be Bb, and 1/4 should be bb.

This conclusion is often expressed as a genotypic ratio: 1 BB:2Bb:1bb. This means that we are predicting that, for every BB baby, they should have 2 Bb babies (twice as many), and one bb baby.

Step Five: Figure out the genotypic ratio for your predicted babies.

Notice that dominance hasn't entered into the problem yet (other than in the application of the Five Rules to figure out the genotypes of the parents). Now it's time to consider dominance.

If you look back at the Five Rules, you'll note that the question you were asked wasn't about genotypic ratios. You were asked to figure out what fraction of their babies would be expected to be brown. This means that you have to figure out the phenotypic ratio.

Step Six: Figure out the phenotypic ratio for your predicted babies.

To do this, you need to ask yourself one question: do any of these different genotypes produce the same phenotype? In other words, do any of these babies look alike? This is where dominance enters the picture. If B is completely dominant to b, all gerbils with at least one B will look pretty much alike, no matter whether their second allele is B or b. So BB and Bb have the same phenotype, and we can add them together. Thus, our phenotypic ratio is 3 Brown:1 Black. Or, there should be three times as many brown babies as black babies.

So the answer to our question is, 3/4 of the babies should be brown.