
- •Парная регрессия. Точечные оценки параметров в условиях классической нормальной модели.
- •Интервальные оценки параметров линейной регрессии.
- •Интервальная оценка средних и индивидуальных значений объясняемой переменной при заданном значении объясняющей переменной.
- •Проверка гипотезы о значимости коэффициентов линейной регрессии. Оценивание качества приближения с помощью коэффициента детерминации.
- •Коэффициент детерминации.
- •Проверка гипотезы о значимости уравнения регрессии в целом.
Интервальная оценка средних и индивидуальных значений объясняемой переменной при заданном значении объясняющей переменной.
Рассмотрим уравнение
y
= a0+a1x+
при некотором фиксированном значении
x
= x0.
Тогда среднее значение
 случайной величины y
равно a0+a1x0,
а индивидуальное a0+a1x0+.
Для оценки этих величин естественно
использовать соотношения b0+b1x0
и соответственно b0+b1x0+
случайной величины y
равно a0+a1x0,
а индивидуальное a0+a1x0+.
Для оценки этих величин естественно
использовать соотношения b0+b1x0
и соответственно b0+b1x0+
Найдем законы
распределения этих случайных величин
и характеристики. Рассмотрим сначала
случайную величину
 .
.
Найдем ковариацию случайных величин
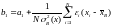 и
и
 .
.
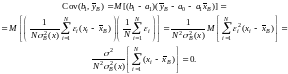
Следовательно,
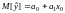 ,
,
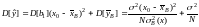 ,
,
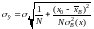 .
.
Можно показать,
что случайные величины
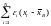 и
и
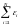 являются независимыми, следовательно,
случайная величина
являются независимыми, следовательно,
случайная величина
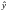 распределена по нормальному закону.
Если взять в качестве оценки параметра
статистику s
то получим, что случайная величина
распределена по нормальному закону.
Если взять в качестве оценки параметра
статистику s
то получим, что случайная величина
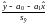 ,
,
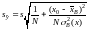 ,
,
распределена по закону Стьюдента с N2 степенями свободы.
Интервальная оценка с доверительной вероятностью средних значений переменной y при x = x0.
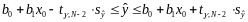 .
.
Для
индивидуальных значений переменной y
все аналогично. Дисперсия случайной
величины
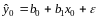 равна
равна

и интервальная оценка индивидуальных значений имеет вид
 ,
,
Где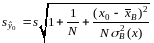 .
.
Проверка гипотезы о значимости коэффициентов линейной регрессии. Оценивание качества приближения с помощью коэффициента детерминации.
Выше мы оценивали параметры линейной регрессии в условиях классической нормальной модели. Статистики, используемые для оценивания коэффициентов линейной регрессии, зависят от стохастической части регрессионной зависимости . Даже если истинные значения параметров a1 и a0 равны нулю, реализации случайных величин b1 и b0, как правило, будут отличаться от нуля. Если параметры a1 и a0 равны нулю, мы будем называть их незначимыми. Наша задача – сформировать процедуру проверки гипотезы о незначимости коэффициентов линейной регрессии и уравнения регрессии в целом по найденным точечным оценкам параметров b1 и b0.
Статистическая гипотеза– высказывание о свойствах генеральной совокупности. Например, статистической гипотезой является предположение о том, что коэффициент a1 в уравнении регрессии равен нулю.
Ошибка 1–го рода– это отказ от гипотезы в случае, когда она верна. Ошибка 2–го рода– принятие гипотезы в случае, когда она не верна. Вероятность сделать ошибку 1–го рода при проверке гипотезы с помощью некоторого критерия называется уровнем значимости критерия. Вероятность не сделать ошибку 2–го рода называется мощностью критерия.
Любой возможный критерий проверки гипотезы о значимости коэффициентов регрессии основан на свойствах распределения случайных величин b1, b0 и s2. Напомним, что случайные величины
,
распределены по закону Стьюдента с числом степеней свободы, равным N 2. В частности, если a1 = 0, то вероятность события

равна
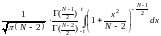 .
.
Напомним, что критической точкой распределения Стьюдента с числом степеней свободы n и доверительной вероятностью называется решение уравнения
Следовательно,
если гипотеза о равенстве нулю коэффициента
a1
верна, то вероятность уклонения величины
 от нуля на величину
от нуля на величину
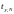 не превосходит =
1.
Это дает следующий простой критерий
проверки гипотезы о незначимости
коэффициента a1
на уровне значимости .
Если
не превосходит =
1.
Это дает следующий простой критерий
проверки гипотезы о незначимости
коэффициента a1
на уровне значимости .
Если
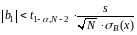 ,
то гипотеза о равенстве нулю коэффициента
a1
принимается. Иначе, гипотеза отвергается,
и коэффициент a1
считается существенно отличным от нуля.
Действительно, ошибку первого рода мы
сделаем лишь в том случае, когда отвергнем
гипотезу, то есть при условии
,
то гипотеза о равенстве нулю коэффициента
a1
принимается. Иначе, гипотеза отвергается,
и коэффициент a1
считается существенно отличным от нуля.
Действительно, ошибку первого рода мы
сделаем лишь в том случае, когда отвергнем
гипотезу, то есть при условии
 .Но
вероятность этого события заведомо не
превосходит величины
.Но
вероятность этого события заведомо не
превосходит величины
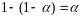 .
Следовательно, уровень значимости
критерия равен .
.
Следовательно, уровень значимости
критерия равен .
Аналогично формулируется критерий проверки гипотезы о значимости коэффициента a0. Если
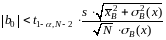
то гипотеза о равенстве нулю коэффициента a0 принимается. Иначе, гипотеза отвергается, и коэффициент a0 считается существенно отличным от нуля.
