Парная регрессия. Точечные оценки параметров в условиях классической нормальной модели.

Предположим, что мы изучаем одновременно две случайные величины 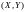. Пусть в результате испытания нами получено N пар наблюдений 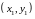, , 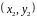, , среди которых могут быть и совпадающие. Вопрос: зависят ли эти две случайные величины друг от друга, и, если зависят, то каков характер этой зависимости?

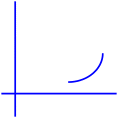
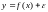
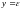
Детерминированная Стохастическая Стохастичность

зависимость зависимость

Предположим, что между y и x имеется стохастическая зависимость вида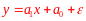

где  – нормально распределенная случайная величина, не зависящая от x. Эти предположения называются классической нормальной регрессионной моделью. Наша задача – по данным наблюдений дать наилучшую оценку параметров a₁ и a₀. Теорема Гаусса–Маркова утверждает, что статистическая оценка с наименьшей дисперсией (то есть эффективная оценка) может быть получена методом наименьших квадратов Гаусса.

Пусть 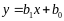– произвольная прямая на плоскости 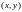. Будем измерять совокупное расстояние от системы наблюдаемых точек выборки до прямой с помощью функции Гаусса

Принцип наименьших квадратов заключается в том, чтобы в качестве параметров b₀ и b₁ выбрать решение задачи

Поскольку функция квадратичная и выпуклая, у задачи имеется единственное решение. По теореме Ферма в точке минимума имеем

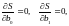
откуда следует, что

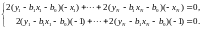
После приведения подобных слагаемых, получаем:

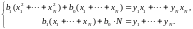
Коэффициенты этой системы можно интерпретировать в статистических терминах. Вспомним, что

, , .

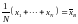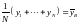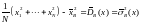Тогда систему последнюю систему уравнений можно записать в виде

Исключая переменную b, получим

 .

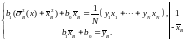
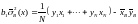В результате получаем формулу для оценки параметра a₁:

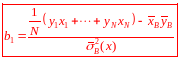
Для параметра a₀ получаем оценку:

Уравнение регрессии удобно записать в следующем виде. Обозначим ,

,

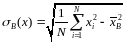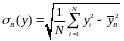
Коэффициент 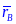называется выборочным коэффициентом корреляции. Тогда функция регрессии задается уравнением

Формулы, полученные для оценки параметров a₀ и a₁ линейной части стохастической зависимости y от x в классической нормальной регрессионной модели, являются состоятельными и несмещенными.

Статистика является состоятельной оценкой некоторого параметра  генеральной совокупности, если выполнено соотношение .

Иными словами, является случайной величиной, вероятность уклонения которой от параметра на произвольно малое расстояние  стремится к нулю с ростом объема выборки N. Реализацию случайной величины принимают за статистическую оценку параметра  по выборке . Оценка является несмещенной, если .

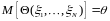Докажем состоятельность оценки b₁. Для этого вычислим математическое ожидание и дисперсию b₁, а затем воспользуемся неравенством Чебышева.

Получаем:

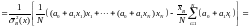
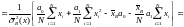
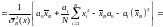
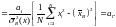
Здесь использовано то обстоятельство, что величины 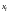являются неслучайными, и . Таким образом, оценка b₁ для параметра a₁ является несмещенной.

Прежде чем вычислять дисперсию случайной величины b₁, преобразуем b₁ к следующему виду

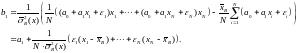
Вспоминая, что дисперсия суммы независимых случайных величин равна сумме их дисперсий, а постоянный множитель выносится из–под знака дисперсии с квадратом, получаем:

Поскольку выбор значений x_i в выборке (x_i,y_i) можно контролировать (переменные x_i можно считать детерминированными), при неограниченном увеличении объема выборки N дисперсия статистики b₁ стремится к нулю как 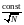. В силу неравенства Чебышева

,

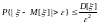получаем, что оценка b₁ является состоятельной, то есть

.

ЗАМЕЧАНИЕ. Сумма любого числа нормально распределенных независимых случайных величин распределена по нормальному закону. В силу соотношения

,

статистика b₁ распределена нормально с математическим ожиданием a₁ и средним квадратичным уклонением . Здесь параметр  есть среднее квадратичное уклонение нормально распределенных случайных величин _i. Таким образом,

Теперь мы можем дать оценку параметра  случайных величин _i. Если бы случайные величины _i были наблюдаемы, и их реализации в статистическом эксперименте оказались бы равны 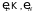, то самой простой состоятельной и несмещенной оценкой дисперсии и, соответственно, среднего квадратичного уклонения каждой из этих величин были бы статистики

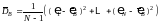и

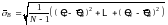
соответственно. С учетом соотношения , статистическим наблюдением случайной величины _i является величина . Однако эта величина не является наблюдаемой, и вместо нее мы можем наблюдать лишь величину 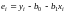. Вычислим, реализацией какой случайной величины является . Подставляя формулы

, ,

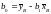получаем

.

Подставляя, в свою очередь, соотношения

,

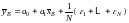
окончательно получаем

.

Легко вычислить математическое ожидание для статистик : . Сложнее вычислить дисперсию 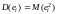. При случайные величины , являются независимыми, поэтому 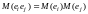. Поскольку , получаем . Следовательно, в выражении 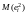ненулевыми являются только математические ожидания “чистых” квадратов 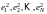. С учетом соотношения

,

получаем

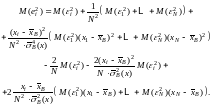
Подставляя 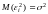, получим

При вычислении были использованы два тождества

, .

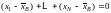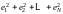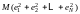Составим так называемую остаточную сумму квадратов, то есть величину , и вычислим . Суммируя по i, получим

Следовательно, несмещенной оценкой параметра  случайной величины  является статистика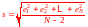 .