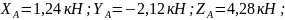- •Вариант № 60 Задача с-1
- •Задача с-2
- •Задача с-3
- •1. Рассмотрим равновесие узла h, в котором сходятся стержни 1, 2. 3.
- •2. Рассмотрим равновесие узла м.
- •Задача к-1
- •2. Скорость и ускорение точки
- •3. Касательное и нормальное ускорение точки при
- •4. Радиус кривизны траектории при
- •Задача к-2
- •Построение плана скоростей начнем с ведущего звена ав.
- •2. Построим план ускорений механизма.
- •Задача д-1
- •Рассмотри движение груза на участке ав, считая его материальной точкой.
- •Рассмотрим теперь движение груза на участке bc.
Вариант № 60 Задача с-1
Конструкция состоит из жесткого угольника и стержня, которые в точке С свободно опираются друг на друга (рис. С2.6). Внешними связями, наложенными на конструкцию, являются шарнир в точке В и жесткая заделка в точке А.
На конструкцию действуют: пара сил с моментом М = 60 кН-м, равномерно распределенная нагрузка интенсивности q = 20 кН/м на участке СL и еще две силы в точке H и K.
Определить реакции связен в точках А, В, С, вызванные заданными нагрузками. При окончательных расчетах принять а = 0,3 м.
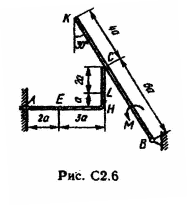
Дано:
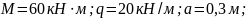
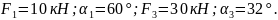
Решение:
Для
определения реакций расчленим систему
и рассмотрим сначала равновесие
угольника
AHC
(рис.
С.2.6,а).
Проведем
координатные оси ху
и
изобразим действующие на стержень силы:
силу
 ,
,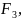 реакцию
реакцию
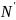 ,
направленную
перпендикулярно стержню КВ,
и составляющие
,
направленную
перпендикулярно стержню КВ,
и составляющие
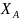 и
и
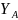 реакции
и момент
реакции
и момент
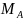 заделки А.
Также на участке CL
действует равномерно распределенная
нагрузка, которую заменяем силой Q,
которая
приложена в середине участка KL
(
заделки А.
Также на участке CL
действует равномерно распределенная
нагрузка, которую заменяем силой Q,
которая
приложена в середине участка KL
(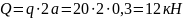 ).
Для
полученной плоской системы сил составляем
три уравнения равновесия:
).
Для
полученной плоской системы сил составляем
три уравнения равновесия:
 а)
б)
а)
б)
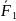

K


 С
С 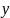



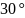
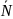
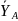
 q
C
q
C
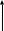
L




 M
M
A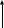
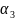 H
H
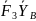
 B
B

Рис. С.2.6

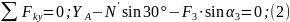
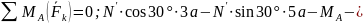
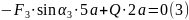
2.
Теперь
рассмотрим
равновесие стержня (рис. С.2.6,б).
На
него действует сила
,
реакция опоры
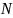 ,направленная
перпендикулярно стержню,
пара
сил с моментом М
и
составляющие
,направленная
перпендикулярно стержню,
пара
сил с моментом М
и
составляющие
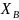 и
и
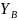 реакции
шарнира B.
реакции
шарнира B.
Для этой плоской системы сил тоже составляем три уравнения равновесия:
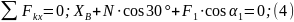
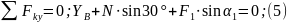

Из уравнения (6) найдем

С учетом найденного значения из остальных уравнений системы вычисляем
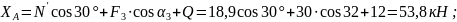
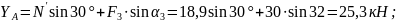
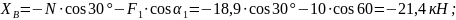
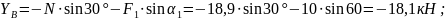
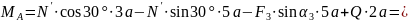
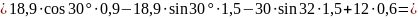
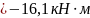
Ответ:
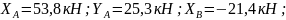
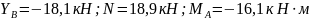

Задача с-2
Две однородные прямоугольные тонкие плиты жестко соединены (сварены) под прямым углом друг к другу к закреплены сферическим шарниром в точке А, цилиндрическим шарниром в точке В и невесомым стержнем (рис. С4.6); стержень прикреплен к плите и к неподвижной опоре шарнирами.
Размеры плит указаны на рисунках; вес большей плиты P1 = 6 кН, вес меньшей плиты Р2 = 5 кН. Каждая из плит расположена параллельно одной из координатных плоскостей (плоскость ху — горизонтальная) .
На плиты действуют пара сил с моментом М =10 кН-м, лежащая в плоскости одной из плит, и две силы. Значения этих сил, их направления и точки приложения: сила F1 — в плоскости, параллельной xy, приложена в точке E и сила F2 — в плоскости, параллельной xz, приложена в точке H. Точка E находится в середине стороны плиты.
Определить реакции связей в точках А и B и реакцию стержня. При подсчетах принять а = 0,6 м.
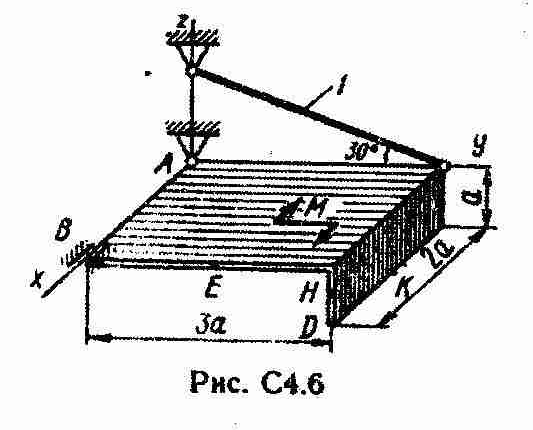
Дано:
Р1
= 6
кН;
Р2
= 5
кН;
М
=
10 кН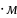 ;
;

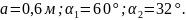
Найти:

Решение:
Рассмотрим равновесие плиты. На плиту действуют заданные силы
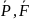 и пара с моментом М
,
а также реакции связей. Реакцию подшипника
в точке В
разложим на две составляющие, лежащие
в плоскости перпендикулярной оси
подшипника. Реакция шарнира в точке А
имеет три составляющие, направленные
по всем трем координатным осям. Реакцию
стержня
направим вдоль него, предполагая, что
он растянут (рис.
С.4.6.б).
и пара с моментом М
,
а также реакции связей. Реакцию подшипника
в точке В
разложим на две составляющие, лежащие
в плоскости перпендикулярной оси
подшипника. Реакция шарнира в точке А
имеет три составляющие, направленные
по всем трем координатным осям. Реакцию
стержня
направим вдоль него, предполагая, что
он растянут (рис.
С.4.6.б).
 z
z


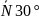


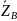 A
A



 y
y
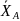 M
M
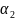
B 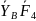
x 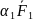

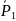
Рис С.4.6.б)
2. Для определения шести неизвестных реакций составляем шесть уравнений равновесия действующей на плиту пространственной системы сил:
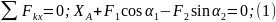
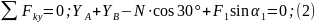
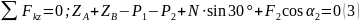

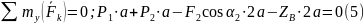
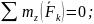

Сразу из 1-го уравнения системы видим:
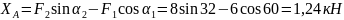
Из уравнения (4) следует:
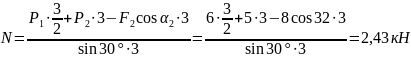
Из уравнения (5) вычислим:

Из уравнения (6) находим:
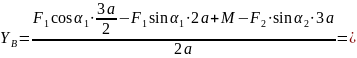

Подставляя в уравнение (2) и (3) найденные значения, определяем:
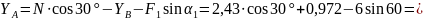
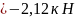


Ответ: