Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

Московский государственный технический университет имени Н.Э. Баумана» (МГТУ им. Н.Э. Баумана)

ФАКУЛЬТЕТ «РАДИОЭЛЕКТРОНИКА И ЛАЗЕРНАЯ ТЕХНИКА» (РЛ)

КАФЕДРА «РАДИОЭЛЕКТРОННЫЕ СИСТЕМЫ И УСТРОЙСТВА» (РЛ-1)

РАСЧЕТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

По курсовой работе

на тему:

Влияние паразитных емкостей и индуктивностей на работу преобразователя постоянного напряжения.

Исполнитель проекта ____________ ______________

(Подпись, дата) (И.О. Фамилия)

Группа Вариант

Руководитель проекта ____________ ______________

(Подпись, дата) (И.О. Фамилия)

Нормок

онтролер ____________ ______________

Москва. 2014

ОГЛАВЛЕНИЕ Часть 1.

Часть 1. Расчет и моделирование схемы понижающего преобразователя постоянного напряжения в программах схемотехнического моделирования Microcap 9 demo и математическом пакете mcad.

1.1. Основы работы понижающего преобразователя постоянного напряжения.

Схема понижающего преобразователя состоит из двух управляющих ключей, один из которых состоит в качестве элемента в управляющем устройстве и интегрирующей цепи.

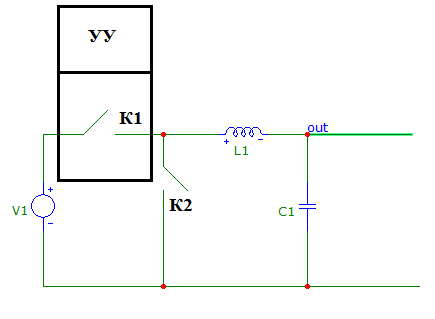
Рисунок 1. Принципиальная схема преобразователя.

Ключи К1 и К2 открываются и закрываются только поочередно, т.е. когда разомкнут ключ К1, К2 обязательно замкнут.

В интервале, когда К1 открыт, происходит накопление энергии в катушке индуктивности и емкости. При закрытии транзистора катушка индуктивности и емкость выступает в роли источника энергии и начинают разрежаться через ключ К2.

Ключи К1 и К2, связанные с управляющим устройством, участвуют в процессе формирования прямоугольных импульсов.

Для наглядности, покажем реакцию такой интегрирующей цепи на единичный прямоугольный импульс:

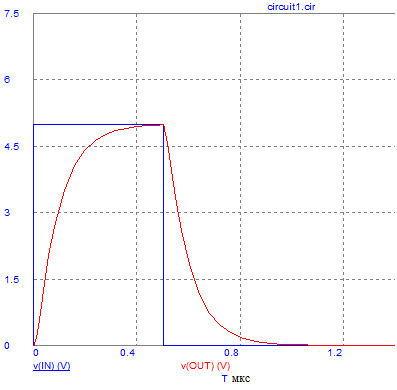
Рисунок 2. Реакция интегрирующей цепи на прямоугольный импульс.

Рассчитаем постоянную времени такой цепи. Включим в схему сопротивление, равное 1 кОм.

Далее будем писать вместо , подразумевая зависимость от времени.

Тогда:

Полное напряжение на конденсаторе является суммой вынужденного и свободного напряжения:

Поэтому:

Запишем характеристическое уравнение:

Положим что разряд конденсатора предельно-апериодический. Тогда

Таким образом мы нашли условие выбора номиналов емкости и индуктивности. Пусть тогда , а .

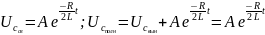
Теперь рассмотрим начальные условия:

В начальный момент времени конденсатор разряжен. Тогда на промежутке времени , напряжение на конденсаторе будет равно:

А при будет равно другому выражению:

Таким образом:

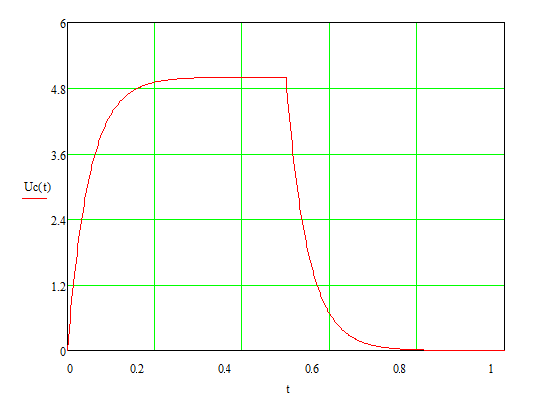
Рисунок 3. Результаты расчетов реакции цепи в MathCad.

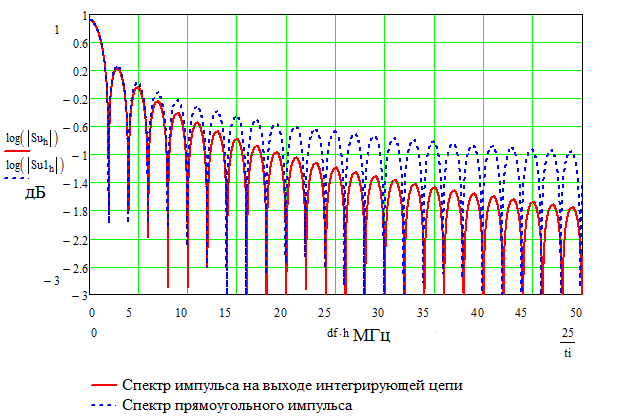
Рисунок 4. Модуль спектральной плотности сигнала на выходе и на входе.

После прохождения импульса через интегрирующую цепочку можно заметить следующее: в спектре импульса амплитуда ВЧ составляющих уменьшилась(для частот ), с другой стороны во временной области фронт импульса стал пологим. Соответственно можно сделать вывод, что ВЧ составляющие в спектре импульса отвечают за формирование формы фронта(постоянную времени фронта).В свою очередь нули спектра импульса не изменяют своего положения по частоте. Что означает, что длительность импульса не изменяется.

Спектр выходного сигнала равняется произведению спектра входного сигнала и АЧХ устройства.

Соответственно можно на активных элементах сделать устройство которое изменяет амплитуду частотных составляющих, либо добавляет «нули».

Постоянная времени такой цепи:

В данном случае можно считать, что период последовательности прямоугольных импульсов много больше постоянной времени цепи. Это значит что конденсатор успевает полностью разрядиться к моменту прихода переднего фронта следующего импульса. Если уменьшить период прямоугольных импульсов, то конденсатор не успеет разрядиться.

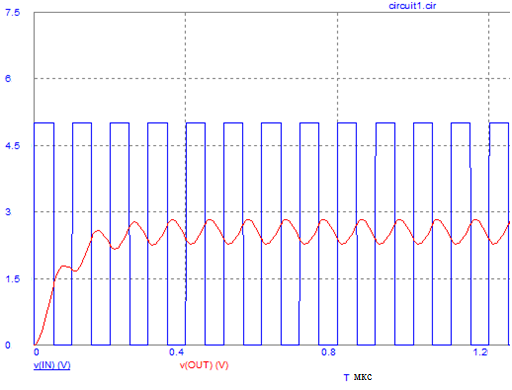
Рисунок 5. Реакция цепи на последовательность импульсов.

Для расчета цепи в случае последовательности импульсов, воспользуемся операторным методом.

Сопротивление катушки будет равным , а конденсатора

Тогда

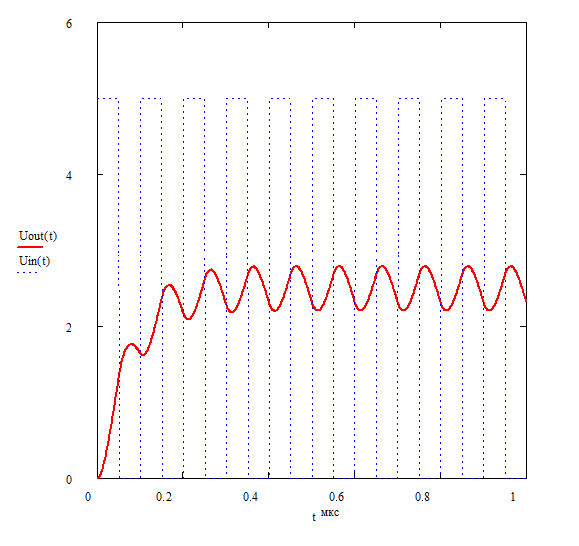
Рисунок 6. Результаты расчетов в MathCad.

Если аппроксимировать напряжение на конденсаторе, то получится, что уровень напряжения на выходе, равен среднему значению напряжения за период. Это значит, что если устройство управления меняет скважность входного сигнала, то будет меняться и напряжение на выходе.