Программа для перестроение таблицы и добавления в неё ещё 1 столбец.

qz=0.3;% выбрали уровень значимости

ResTabl=Tabl (1,1:6);% взяли первую строку

for k1=2:k, % берем остальные строки таблицы

if ResTabl (end, 6)<5, % предыдущее npj<5 – будем суммировать

ResTabl (end, 3)=Tabl (k1,3);% новая правая граница интервала

ResTabl (end, 4:6)=ResTabl (end, 4:6)+Tabl (k1,4:6);% суммируем

else% предыдущее npj>=5 – будем дописывать строку

ResTabl=[ResTabl; Tabl (k1,1:6)];% дописываем строку

end

if ResTabl (end, 6)<5, % последнее npj<5

ResTabl (end – 1,3)=ResTabl (end, 3);% новая правая граница

ResTabl (end – 1,4:6)=ResTabl (end – 1,4:6)+ResTabl (end, 4:6);

ResTabl=ResTabl (1:end-1,:);% отбросили последнюю строку

end

kn=size (ResTabl, 1);% число объединенных интервалов

ResTabl(:, 1)=[1:kn]';% новые номера интервалов

ResTabl(:, 7)=(ResTabl(:, 4) – ResTabl(:, 6)).^2./ResTabl(:, 6);

disp ('Сгруппированная сводная таблица результатов')

fprintf (' j aj bj')

fprintf (' nj pj npj ')

fprintf([' (nj-npj)^2/npj\n'])

fprintf (' % 2.0f % 12.5f % 12.5f % 6.0f % 12.5f % 12.5f % 12.5f\n', ResTabl')

hi2=sum (ResTabl(:, 7));% сумма элементов последнего столбца

fprintf(['Статистика Пирсона chi2=%10.5f\n'], hi2)

m=[3,2,3,2];% число ограничений

fprintf ('Задаем уровень значимости q=%5.4f\n', qz)

chi2qz=chi2inv (1-qz, kn-m(bdistr));% квантиль

fprintf(['Квантиль chi2-распределения Пирсона '…

'chi2 (1-q)=%10.5f\n'], chi2qz)

if hi2<=chi2qz,

disp ('Распределение подобрано верно, т. к. chi2<=chi2 (1-q)')

else

disp ('Распределение подобрано неверно, т. к. chi2>chi2 (1-q)')

end

Статистика Пирсона chi2= 4347.29975

Задаем уровень значимости q= 0.3000

Квантиль chi2-распределения Пирсона chi2 (1-q)= 170.93451

Распределение подобрано неверно, т. к. chi2>chi2 (1-q)

Вывод: По критерию Пирсона распределение подобрано неверно, т. к. реальное значение статистики χ²_р=4347.29975 намного превышает критическое значение χ²_т,f=170.93451, следовательно, гипотеза о нормальном законе распределения амплитуд сигнала не подтверждается на уровне значимости 0.05.

Статистика Пирсона chi2= 325.28014

Задаем уровень значимости q=0.3000

Квантиль chi2-распределения Пирсона chi2 (1-q)= 194.58370

Распределение подобрано, верно, т. к. chi2<=chi2 (1-q)

Вывод: Для фонового сигнала по критерию Пирсона распределение подобрано неверно, т. к. реальное значение статистики χ²_р=325.28014 превышает критическое значение χ²_т,f=194.58370, следовательно, гипотеза о нормальном законе распределения амплитуд сигнала не подтверждается на уровне значимости 0.05.

2. Корреляционный анализ сигналов

2.1 Постановка задачи исследования

Для этого принять сигнал за реализацию случайной функции, выбрать наиболее яркий фрагмент сигнала длительностью 2000 отсчетов и построить для него корреляционную функцию. Для сигналов человека и группы людей оценить квазипериодическую составляющую, а для сейсмического фона и техники – периодическую. Сделать выводы о внутренней структуре сигнала. Сделать выводы по этапу.

2. Теоретическая часть. Свойства корреляционной функции

Корреляционный анализ дает возможность установить в сигналах (или в рядах цифровых данных сигналов) наличие определенной связи изменения значений сигналов по независимой переменной, то есть, когда большие значения одного сигнала (относительно средних значений сигнала) связаны с большими значениями другого сигнала (положительная корреляция), или, наоборот, малые значения одного сигнала связаны с большими значениями другого (отрицательная корреляция), или данные двух сигналов никак не связаны (нулевая корреляция).

В функциональном пространстве сигналов эта степень связи может выражаться в нормированных единицах коэффициента корреляции, т.е. в косинусе угла между векторами сигналов, и, соответственно, будет принимать значения от 1 (полное совпадение сигналов) до -1 (полная противоположность) и не зависит от значения (масштаба) единиц измерений.

Особое значение методы корреляции имеют при анализе случайных процессов для выявления неслучайных составляющих и оценки неслучайных параметров этих процессов.

Заметим, что в терминах "корреляция" и "ковариация" в настоящее время существует изрядная путаница. В иностранной литературе термин "ковариация" применяется к центрированным функциям, а "корреляция" – к произвольным. В отечественной литературе, и особенно в литературе по сигналам и их обработке, довольно часто применяется прямо противоположная терминология. Однако при переводах иностранной литературы терминология, как правило, не изменяется, и начинает все шире проникать в отечественную литературу. Принципиального значения это не имеет, но при знакомстве с литературными источниками стоит обращать внимание на принятое назначение данных терминов.

Свойством корреляционной функции является ее убывание с увеличением t, что вытекает из очевидного факта ослабления взаимной связи между случайными величинами л: ( 0) и x ( t) по мере увеличения временного интервала At - t между ними. Если при этом корреляционная функция стремится к нулю, говорят, что характеризующийся ею стационарный случайный процесс обладает свойством эргодичности. Это удобно при практическом выполнении и обработке наблюдений.  Из свойств корреляционной функции / Сф ( i) следует, что спектральная плотность мощности 5Ф ( ал) является вещественной, четной и положительной функцией.  Хотя многие свойства корреляционных функций тесно связаны со свойствами корреляционных функций в классической теории, существуют некоторые свойства квантовых корреляционных функций, которые не имеют классической аналогии. Например, так как операторы нормально упорядочены, то последовательное применение операторов уничтожения справа или операторов рождения слева приведет к обращению корреляционной функции в нуль, если состояние содержит число фотонов меньшее, чем число операторов. 

2.3 Программа и результат корреляционной функции

Для построения корреляционной функции двух сигналов, выберем фрагменты сигналов:

Программа предназначена для построения корреляционной функции двух сигналов.

%Начало фрагмента задается величиной N1

N1=25001;

% конец фрагмента задается величиной N2

N2=26000;

x=h3_r10 (N1:N2); %вырезали фрагмент сигнала

r=xcorr (x, x); %Вычисление корреляционной функции

На рисунке 10 представлен график исходного сигнала человека.

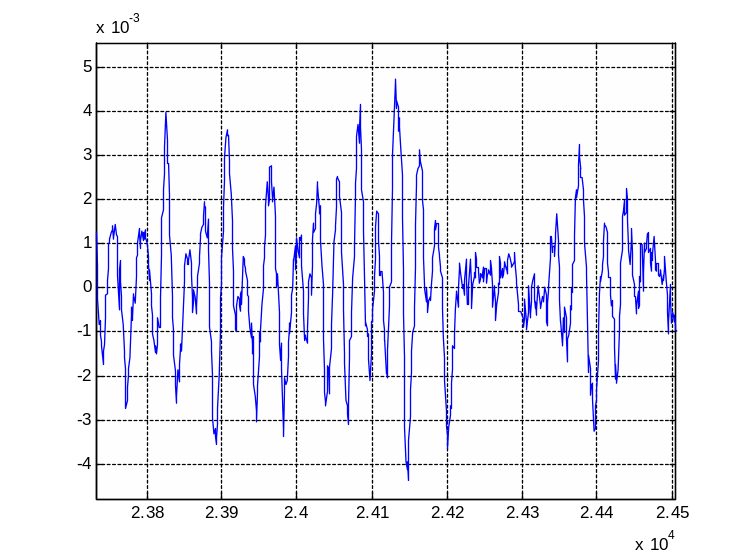
Рисунок 10 – График исходного сигнала человека

Для сигнала человека выбираем наиболее информативный участок от 24000 до 25000

На рисунке 11 изображен график исходного фонового сигнала.

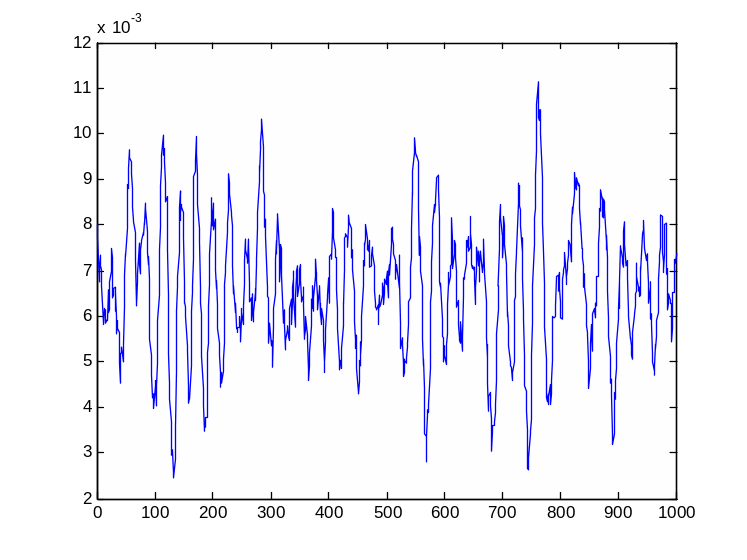
Рисунок 11 – График исходного фонового сигнала

Для фонового сигнала выбираем наиболее информативный участок то 25000 до 26000.

Программа для сигнала человека

h1=h3_r10 (54000:55000);% вырезали фрагмент

k=1000;

KF=xcorr (h1, h1, k);% КФ

k1=-k:k; plot (k1, KF);%построили КФ

На рисунке 12 изображен график корреляционной функции человека.

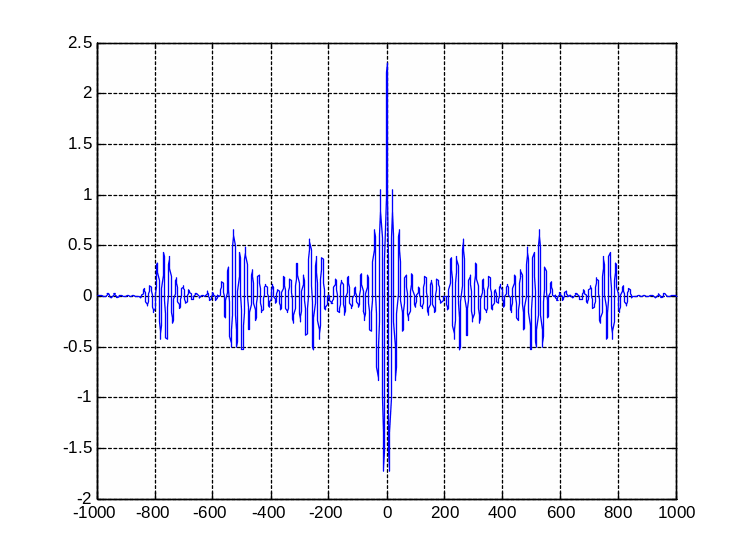
Рисунок 12 – График корреляционной функции человека

Вывод: График имеет квазипериодический характер. Повтор явных всплесков колебаний через каждые 250÷300 отсчетов. По корреляционной функции также можно сказать, что сигнал имеет колебательный случайный характер. Так же можно сказать, что функция не стационарна, так как дисперсия ее не постоянна. Период колебания корреляционной функции сигнала человека составляет примерно 290 отсчетов (0.58 с).

Программа для фонового сигнала

h2=h3_r10 (15000:16000);% вырезали фрагмент

k=1000;

KF=xcorr (h2, h2, k);% КФ

k1=-k:k; plot (k1, KF);%построили КФ

На рисунке 13 представлен график корреляционной функции фонового сигнала.

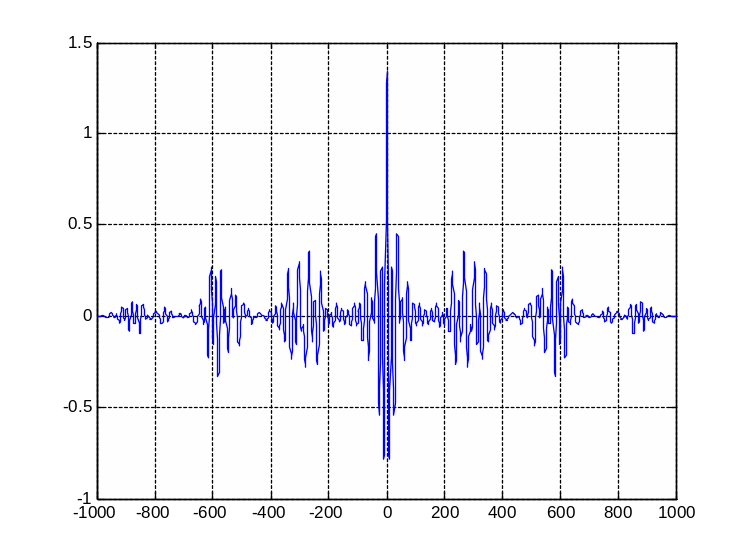
Рисунок 13 – График корреляционной функции фонового сигнала

Вывод: по корреляционной функции для фонового сигнала можно сказать, что сигнал имеет колебательный случайный характер. Так же можно сказать, что функция не стационарна, так как дисперсия ее не постоянна. Период колебания корреляционной функции фонового сигнала составляет приблизительно 190 отсчетов.

3. Исследование признаков

3.1 Оценка параметров распределения признаков.

Требуется изучить количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак. Естественно возникает задача оценки параметров, которыми определяется это распределение. Обычно в распоряжении исследователя имеются лишь данные выборки, например, значения количественного признака, полученные в результате  наблюдений. Через эти данные и выражают оцениваемый параметр. Рассматривая  как независимые случайные величины, можно сказать, что найти статистическую оценку неизвестного параметра распределения – это значит найти функцию от наблюдаемых случайных величин, которая и дает приближенное значение оцениваемого параметра.