Глава II випадкові величини і закони розподілу

§ 9. Поняття випадкової величини і закону розподілу

Окрім поняття випадкової події головним поняттям теорії ймовірності є поняття випадкової величини .

Випадковою величиною називається змінна, яка в результаті випробування набуває деяке значення, невідоме до проведення випробування.

Прикладами випадкових величин є:

1. число влучень в ціль при заданій кількості пострілів;

2. кількість телефонних викликів за заданий час;

3. сума виграшу або програшу в азартній грі;

4. час очікування в черзі;

5. витрати палива на перехід з одного порту до іншого;

6. похибки вимірювання будь-якої величини тощо.

Значення випадкової величини залежить від результату випробування тобто від елементарної події, яка сприяє цьому результату. Тому випадкову величину можна визначити і як функцію, задану на множині результатів (елементарних подій) випробування.

Конкретні значення, які може приймати випадкова величина, називаються її можливими значеннями.

Далі випадкові величини будемо позначати великими буквами латинської абетки: , а їх можливі значення відповідно малими: . За характером множини усіх можливих значень випадкові величини можна поділити на дискретні і неперервні.

Випадкова величина називається дискретною, якщо навколо кожного її можливого значення існує окіл, до якого не належать інші можливі значення. У наведених вище прикладах до дискретних відносяться приклади величин 1-3.

Випадкова величина називається неперервною у випадку, коли її можливі значення неперервно заповнюють деякий числовий проміжок. До неперервних величин слід віднести приклади величин 4–6.

Сукупність двох випадкових величин ( ) називається двовимірною випадковою величиною, або двовимірною випадковою точкою, або двовимірним випадковим вектором. Так, положення судна ( ) є випадковою двовимірною величиною, де , – відповідні координати судна.

Аналогічно можна визначити n-вимірний випадковий вектор як впорядковану сукупність випадкових величин .

Дослідження випадкової величини, по-перше, полягає у встановленні множини всіх її можливих значень. По-друге, необхідно знати як часто можуть з’являтися ті чи інші значення випадкової величини в результаті випробувань за однакових умов. Іншими словами, необхідно знати ймовірність появи конкретних можливих значень випадкової величини. Будь-який зв’язок між можливими значеннями випадкової величини і ймовірністю їх появи у випробуванні називається законом розподілу випадкової величини.

Нехай – дискретна випадкова величина, яка при випробуванні може мати значення . Тоді результат випробування складається із елементарних подій:

, . (9.1)

Для ймовірностей цих подій введемо позначення:

.

Якщо ці ймовірності відомі, то закон розподілу випадкової величини можна задати у вигляді наступної таблиці:

						(9.2)

В першому рядку цієї таблиці перелічені всі можливі значення випадкової величини , а у другому – ймовірності цих значень. Причому, оскільки події (9.1) утворюють повну групу подій, то

.

Таблицю (9.2) прийнято називати рядом розподілу.

Користуватися рядом розподілу стає незручно коли випадкова величина має велику кількість можливих значень. Щоб придати ряду розподілу більш наочний вигляд, здійснюють його графічне зображення. Для цього на осі абсцис відкладають можливі значення, а на осі ординат їх ймовірності і будують на площині точки з відповідними координатами. Після цього отримані точки послідовно з’єднують відрізками прямих. Побудована фігура називається многокутником розподілу:

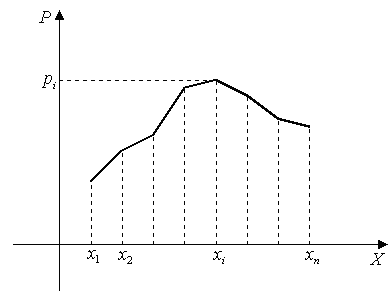
Рис. 4.

Задання закону розподілу у вигляді ряду або многокутника можливе лише у випадку дискретної випадкової величини із скінченою кількістю можливих значень. Задати так закон розподілу неперервної випадкової величини неможливо. По-перше, кількість значень неперервної випадкової величини є нескінченою і не може бути перелічена у таблиці. По-друге, кожне окреме значення неперервної випадкової величини має нульову ймовірність. Для задання закону розподілу неперервної випадкової величини використовують не ймовірність події , а ймовірність того, що , тобто ймовірність того, що випадкова величина у випробуванні прийме значення, менше ніж . Ця ймовірність, зрозуміло, буде функцією від і називається функцією розподілу.

Функцією розподілу випадкової величини називається ймовірність того, що у випробуванні значення цієї величини не буде перевищувати :

. (9.3)

З означення можна бачити, що функцію розподілу можна використовувати і для дискретної випадкової величини. Якщо – дискретна випадкова величина з рядом розподілу (9.2), то

. (9.4)

Нерівність під знаком суми означає, що додаються ймовірності тих значень , які менші ніж .

Побудуємо графік функції розподілу дискретної випадкової величини з рядом розподілу (9.2).

Нехай , тоді – неможлива подія і ;

при

;

на наступному проміжку :

.

Взагалі, для будь-якого проміжку

.

Наприкінці, коли , знаходимо

Таким чином, графік буде мати вигляд:

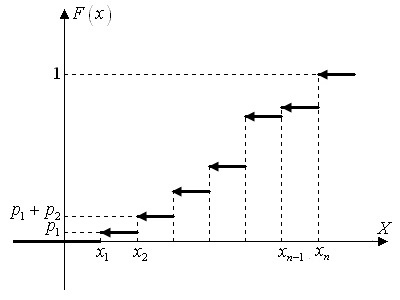
Рис. 5

З наведеного графіка можна бачити, що функція розподілу дискретної величини є розривною. В точках, які співпадають з можливими значеннями, вона має розриви першого роду.