3.2.3. Бесконечно большие последовательности
Рассмотрим
произвольную неограниченную
последовательность
.
Ее предел в обычном смысле не существует.
В этом случае вводится понятие бесконечного
предела.
Определение
3.7. Говорят,
что последовательность
сходится к
при
,
если
существует такой
номер
,
что для всех номеров
выполнено
неравенство
.
Обозначают:
.
Например,
последовательность
сходится к
,
то есть
.
Определение
3.8. Говорят,
что последовательность
сходится к
при
,
если
существует такой
номер
,
что для всех номеров
выполнено
неравенство
.
Обозначают:
.
Например,
последовательность
сходится к
,
то есть
.
Определение
3.9. Говорят,
что последовательность
сходится к
при
,
если
существует такой
номер
,
что для всех номеров
выполнено
неравенство
.
Обозначают:
.
Например,
последовательность
не сходится ни к
,
ни к
,
однако
.
Определение
3.10. Последовательность,
пределом которой является бесконечность
(со знаком или без), называется бесконечно
большой последовательностью,
то есть
.
ТЕОРЕМА 3.3. Справедливы следующие утверждения.
1.
Если
при
,
то
при
.
2.
Если
при
,
то
при
.
3.
Если
при
,
то
при
.
4.
Если
при
,
то
при
.
§3.3. Теоремы о сходящихся числовых последовательностей
ТЕОРЕМА 3.4 (ограниченность сходящейся последовательности). Сходящаяся последовательность ограничена.
Доказательство.
Пусть
последовательность
ограничена и
.
Тогда
.
Так
как
,
то
оставшаяся часть последовательности
имеет наибольшее и наименьшее значения.
Обозначим
,
.
Тогда
выполнено неравенство
.
ТЕОРЕМА
3.5. Если
и
,
то существует номер
такой, что
выполнено
.
Доказательство.
Выберем
и
так, чтобы
-окрестности
точек а
и b
не пересекались. Так как
,
то для всех
выполнено неравенство
.
В
силу определения предела последовательности
существуют номера
и
такие, что
при
и
при
.
Если
взять
,
то при
будет выполнено неравенство
.
Следствие
3.2. Если
существует
и
(или
),
где
,
то существует номер
такой, что для всех
выполнено неравенство
.
ТЕОРЕМА
3.6 (предельный переход в неравенствах).
Пусть
и
сходящиеся последовательности и
.
Тогда
.
Доказательство.
Пусть
и
.
Нужно доказать, что
.
Докажем методом от противного. Предположим,
что
.
По определению
предела последовательности
|
(3.5) |
,
|
(3.6) |
.
Пусть
,
тогда для любого
и для всех номеров
одновременно выполнены неравенства
(3.5) и (3.6), следовательно,
.
Однако
неравенство
не выполняется, например, для
.
Получили противоречие. Значит, предпосылка
неверна и
.
ТЕОРЕМА
3.7 (арифметические действия с пределами).
Если
последовательности
и
имеют конечные пределы
и
,
то последовательности
,
,
,
также сходятся и выполняются равенства:
1)
;
2)
;
3)
,
где
(постоянный множитель можно выносить
за знак предела);
4)
,
если
.
Доказательство.
1) Из определения
предела последовательности следует,
что
выполнено
или
|
(3.7) |
,
|
(3.8) |
.
Возьмём , тогда выполнены неравенства (3.7) и (3.8) одновременно.
сложим правые части неравенств (3.7) и (3.8), тогда
,
то
есть
— это значит, что
.
Утверждение для
доказано.
Для последовательности доказывается аналогично.
2)
По теореме 3.4 обе последовательности
и
ограничены, то есть
выполнено
.
Пусть
и
,
где
.
По определению предела последовательности:
,
где
такое, что
выполняются одновременно неравенства
и
.
При имеем:
.
Таким
образом, мы показали, что
.
3)
Рассмотрим вспомогательную
последовательность
,
и применим доказанное выше равенство
для последовательности
,
учитывая, что
.
4)
Если
,
то
и по следствию 3.2:
.
Если
,
то
,
тогда
.
То
есть последовательность
ограничена.
Последовательность
сходится, а значит ограничена. Поэтому
можно записать неравенства
Пользуясь
определением предела последовательности,
получим, что
одновременно выполняются неравенства:
.
При любом имеем
.
Замечание 3.4. Если последовательности имеют бесконечные пределы или знаменатель дроби стремится к нулю, утверждения из теоремы 3.7 вообще говоря, не имеют места. Приведем примеры.
Примеры.
3.13. Найти предел последовательности при , если:
а)
;
б)
;
в)
;
г)
.
Решение.
а)
здесь
при
,
тогда
;
б)
здесь
при
,
тогда
;
в)
здесь
при
,
тогда
;
г)
здесь
при
,
тогда
— не имеет предела.
3.14. Найти предел последовательности при , если:
а)
;
б)
;
в)
.
Решение.
а)
здесь
при
,
тогда
;
б)
здесь
при
,
тогда
;
в)
здесь
при
,
тогда
— не имеет предела.
3.15. Найти предел последовательности при , если:
а)
;
б)
;
в)
;
г)
.
Решение.
а)
здесь
при
,
тогда
;
б)
здесь
при
,
тогда
;
в)
здесь
при
,
тогда
;
г)
здесь
при
,
тогда
— не имеет предела.
3.16. Найти предел последовательности при , если:
а)
;
б)
;
в)
;
г)
.
Решение.
а) здесь при , тогда ;
б) здесь при , тогда ;
в) здесь при , тогда ;
г)
здесь
при
,
тогда
— не имеет предела.
Замечание 3.5. Случаи, указанные в замечании 3.4 относятся к числу задач с неопределенностью, а их решение называются раскрытием неопределенности.
В
примере 3.13 рассмотрена неопределенность
вида
:
,
тогда
.
В
примере 3.14 рассмотрена неопределенность
вида
:
,
тогда
.
В
примере 3.15 рассмотрена неопределенность
вида
:
,
тогда
.
И,
наконец, в примере 3.16 рассмотрена
неопределенность вида
:
,
тогда
.
Примеры.
3.17.
Найти предел последовательности
.
Решение.
Здесь
,
при
.
Умножим
и разделим на сопряженное выражение:
.
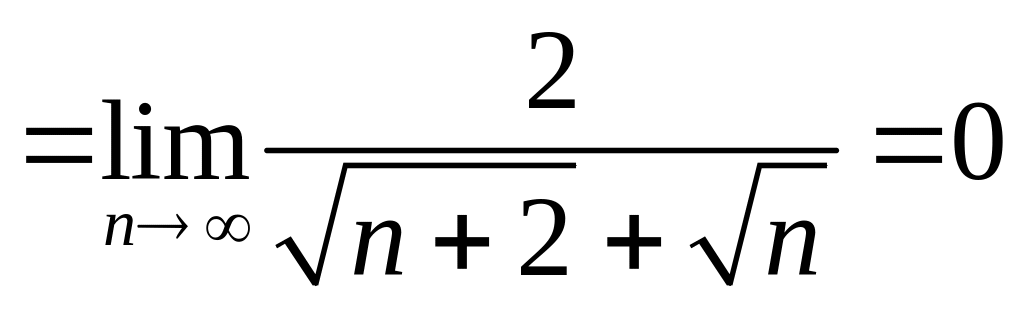3.18.
Найти предел последовательности
.
Решение.
Воспользуемся формулой суммы
(в нашем случае
)
членов арифметической прогрессии:
.
Заметим, что в нашем случае число членов . Тогда
.
3.19.
Найти предел последовательности
.
Решение.
Разделим числитель и знаменатель дроби
на
и воспользуемся тем, что
и
:
.
3.20. Доказать, что если:
1)
,
то
;
2)
,
то
.
Решение.
1)
Для
доказательства, воспользуемся неравенством
Бернулли. Пусть
,
тогда
|
(3.9) |
.
Представим
в виде
,
где
,
тогда из неравенства (3.9) получим
.
Так
как
,
то и
.
2)
Пусть теперь
.
Обозначим
,
значит
и
.
ТЕОРЕМА
3.8 (признак существования предела).
Если
,
и
то последовательность
также сходится и
.
Доказательство. По определению предела последовательности
,
.
Выберем
,
тогда
и
.
В силу неравенства из условия теоремы:
,
значит
.
Отсюда
получим
,
или
для всех
,
что и означает, что
.
Примеры.
3.21.
Доказать, что
для произвольного
.
Решение.
1)
Пусть
.
Тогда
,
т.к. в противном случае
и при
перемножая это неравенство n
раз получим
,
что противоречит условию
.
Положим
,
тогда
и
.
Применим неравенство Бернулли:
,
то
есть
.
Тогда, так как
,
учитывая теорему 3.6, получаем
,
и,
значит,
.
Из теоремы 3.8 следует, что
.
2)
Пусть
.
Обозначим
.
По доказанному для
выполнено
.
Тогда
.
3)
Пусть
,
тогда
и, следовательно,
.
3.22.
Доказать, что
для произвольного
.
Решение. Воспользуемся примером 3.26:
.
3.23.
Вычислить
.
Решение. Воспользуемся очевидным неравенством:
.
Следовательно,
.
Так
как
(см. пример 3.21), то
и по теореме 3.6 получаем, что
.
ТЕОРЕМА
3.9. Если
,
,
,
то
.
ТЕОРЕМА
3.10. Если
,
,
то
.
Пример.
3.24.
Вычислить
предел
.
Решение.
Используя свойство VII,
получаем
.
ТЕОРЕМА
3.11. Если
,
,
,
,
,
то
.