Часть II. Методы управления старением машин

Прикладное значение теории старения машин предполагает три обязательных этапа работы с объ­ектом для поддержании его в работоспособном состоянии:

1. Профилактика - старения материалов, деталей и всей машины.

2. Установление диагноза изменение состояния машины - это техническая диагностика, без которой невозможно установить "рецепты" лечения (ремонтов).

3. Восстановление технического состояния машин - ремонт машин, продлевающий их срок службы (аварийный и плановый).

Глава 4. Конструктивные методы управления старением машин

Современные горные машины эксплуатируют в тяжелых условиях, связанных с ограниченностью габаритов, абразивностью горных пород, запыленностью атмосферы, воздействием агрессивных шахтных вод. Долговечность горной машины зависит не только от тех идей и приемов, ма­териалов и конструкций, которые были заложены при проектировании ма­шины, но и от возможности ее реновации, которая могла быть применена дополнительно в машине при ее ремонтах, и модернизации. Реновация машины на стадии эксплуатации позволяет улучшить, как правило, наиболее нагруженные детали и узлы, повысить за счет этого долговечность и обеспечивает возможность сохранить эффективность использования всей машины, т.е. управлять процессом старения машины.

В процессе реновации конструкции машины соз­даются условия для замедленного ее старения. При этом возможность устранения выявленных ошибок конструктора, которые часть связаны с несовершенством методов конструирования и недостаточно полным учетом условий изготовления и эксплуатации машин.

Ниже подробно рассматриваются методы решения этих проблем.

И, наконец, при эксплуатации машины ее старение будет зависеть от режима работы машины, методов профилактики, применяемых приемов восстановления деталей и системы ремонта машины.

Ниже подробно рассматриваются "рецепты" управления старением машин на всех этих этапах.

4.1. СОВЕРШЕНСТВОВАНИЕ РАСЧЕТОВ ДЕТАЛЕЙ

Типовые расчеты деталей машин на долговечность производятся или по коэффициенту работоспособности: С=Q(n-h)^0,3, где Q - приведенная на­грузка, а h - расчетная долговечность (или , где t_ср - средний срок службы 50 % изделий, R - величина рабочего воздействия), или по ко­эффициенту запаса (запасу прочности) по эквивалентному напряжению (для валов, например, , где _н и _к - наибольшие напряжения соответственно при изгибе и при кручении).

При расчетах на усталостную прочность эквивалентное напряжение рассчитывается по формуле, которая позволяет более полно учесть выявленный при эксплуатации разброс напряжений, цикла нагружений в преобладающем спектре:

,

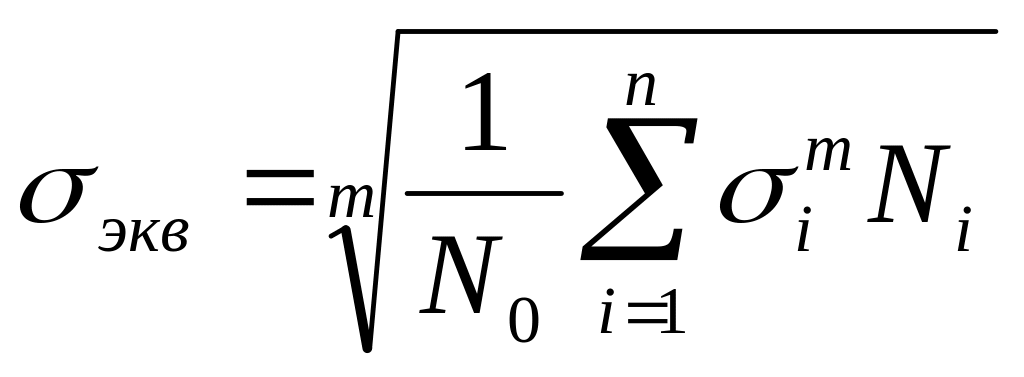где N₀ - число циклов, соответствующее точке перегиба кривой усталости (обычно принимают N₀=(35) 10⁶ циклов), N_i - общее число циклов нагружений при напряжениях _i.

Можно долговечность деталей рассчитать и по приведенному числу циклов нагружений, учитывающему реальный спектр нагрузок и фактическую нагруженность критического элемента по времени ее действия:

,

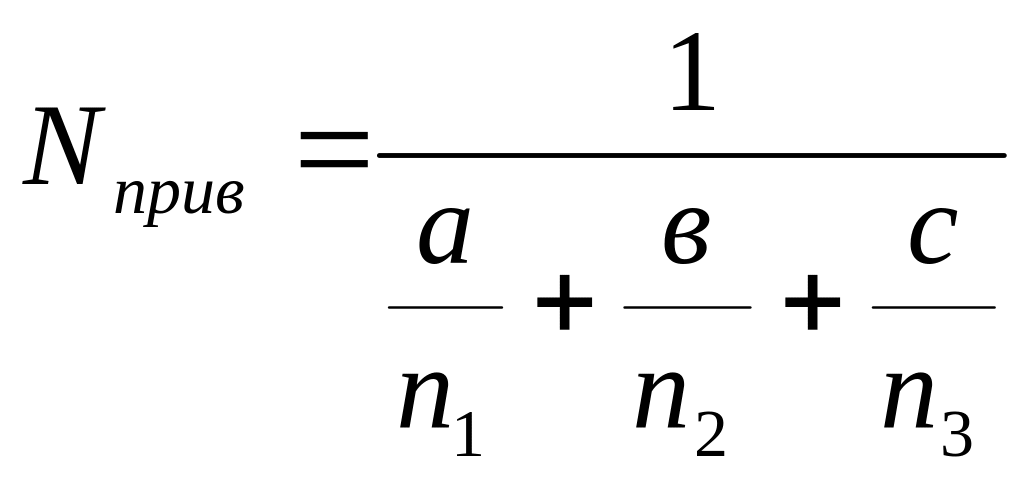где а, в, с - средневзвешенная доля работы при нагрузках, вызывающих соответственно напряжения ₁, ₂, ₃;

n₁, n₂ и n₃ - по диаграмме усталости - число циклов, при которых произойдет разрушение от напряжений ₁, ₂, ₃.

Например, для вала дробящего конуса дробилки нагрузка нормальная в месте посадки 5000 Па, при попадании не дробимого тела (кусок металла) напряжение возрастает до 15000 Па. Коэффициент концентрации: от посадки вала для Ст5 равен 2, от неровностей обработки -1,15.

Напряжение с учетом коэффициента концентрации: _норм=500021,15- 11500 Па; _увелич=1500021,15=34500 Па.

Примем, что дробилка работает на 70 % с полной нагрузкой, 30 % - с половинной, 1 раз в смену попадает недробимое тело.

Определим приведенное число циклов (с учетом N_прив):

.

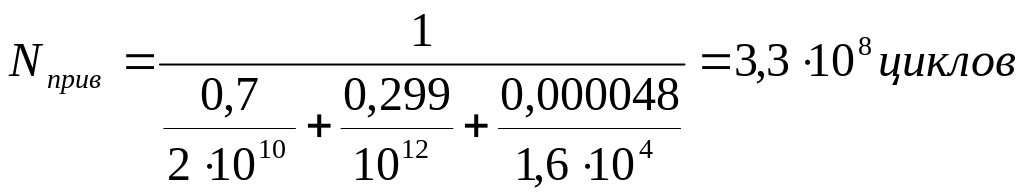Долговечность вала при работе в сутки в течение 20 часов при n = 220 об/мин:

.

Однако даже при таких расчетах не учитывается в полной мере случайный характер действующих нагрузок, изменчивость механических свойств металлов деталей. Если известны параметры рассеяния нагруженности (например, измеренная методом тензометрирования) и характеристик прочности (проведенная ста­тистической обработкой данных сертификатов на металл), то целесообразно расчет на выносливость производить вероятностными методами.

При вероятностном методе расчета выбор запаса прочности определя­ется вероятностью разрушения в течение срока службы машины. Основой вероятностных расчетов является положение о том, что эксплуата­ционные нагрузки носят случайный характер и характеристики сопротивле­ния усталости также являются случайными величинами.

Н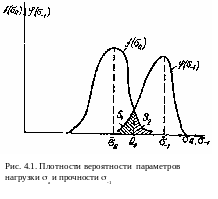 а рис. 4.1 показаны плотности распределения Гаусса параметров нагрузки _а и прочности _-1. Вероятность Р_отказа по разрушению детали пропорциональна левому участку S₁ площади под перекрывающимися участка­ми кривых этих рас­пределений. Эту площадь, а, следова­тельно, и вероятность разрушения можно уменьшить тремя способами:

- снижением напряжений _а за счет увеличения сечения и массы детали, что в большинстве случаев для горных машин недопустимо;

• увеличением среднего значения предела выносливости _-1, что воз­можно за счет удорожания изделия,

• уменьшением дисперсии прочности используемых материалов за счет увеличения однородности и снижения разброса механических свойств металла (например, в сталях электрошлакового переплава или рафинированных синтетическим шлаком, см. ниже).

Достижение прочности с необходимым уровнем безотказности можно гарантировать при вероятностном определении запасов прочности с учетом законов распределения как нагрузок, так и показателей, определяющих прочность деталей.

Условие прочности или условие безотказности означает отсутствие у элемента предельного состояния, т.е. когда прочность соответствует или превосходит нагрузку, что выражается неравенством:

.

При известных законах распределения _а и _-1 вероятность отсутствия отказа у детали вследствие того, что _-1>_а, может быть определена для нагрузки уровня Q_i (см. рис. 4.1) путем интегрирования плотности вероятно­сти f(_-1) распределения показателя прочности:

.

Вероятность непоявления отказа в общем случае определяется из выражения:

,

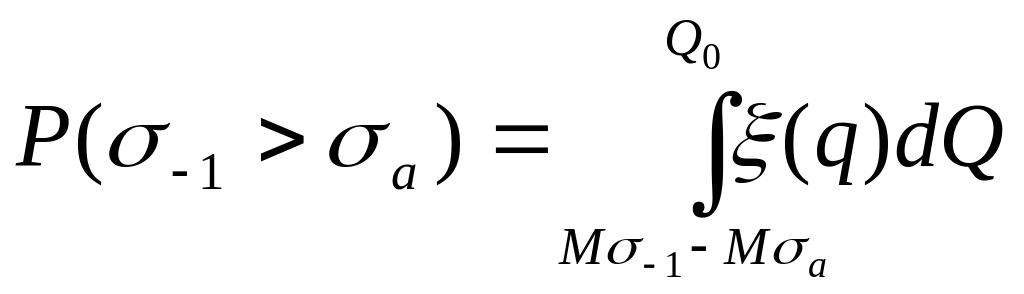где (q) - плотность вероятности случайной величины , представляющей собой композицию законов распределения напряжений _а и _-1 (композиция законов распределения случайных величин называется законом распределения суммы этих величин);

и - математические ожидания показателей прочности и нагруз­ки соответственно.

В частном случае, при подчиненности нормальным законам распределения показателей прочности и нагрузки композиция законов их распределе­ния также будет подчинена нормальному закону распределения:

.

Случайные величины _а и _-1 являются независимыми (нагрузка не за­висит от прочности), поэтому:

_,

где М_q - математическое ожидание случайной величины q;

D² - дисперсии соответствующих величин.

Учитывая это, получим:

.

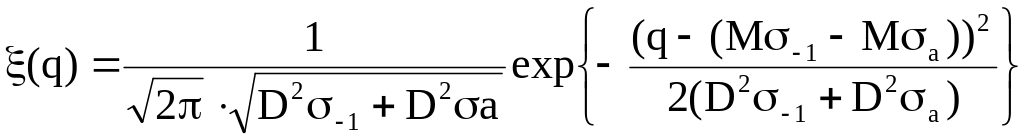Вероятность отсутствия отказа вследствие того, что _-1>_а , опреде­лится (с использованием функции Лапласа):

.

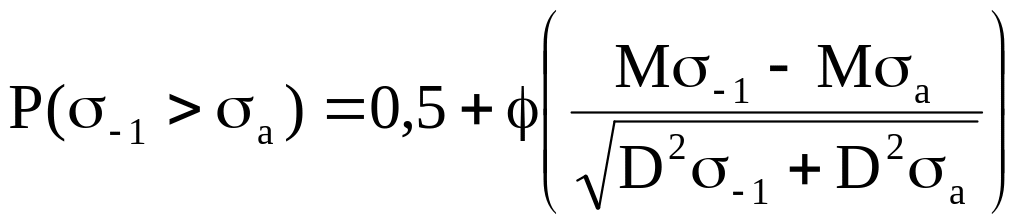При произвольных законах распределения рекомендуется метод приближенного определения вероятности отсутствия отказа рассчитываемого элемента. Вероятность отказа

,

где S₁ - вероятность того, что прочность детали меньше, чем Q₀ (см. рис 4.1), S₂ - вероятность превышения нагрузки уровня Q₀:

;

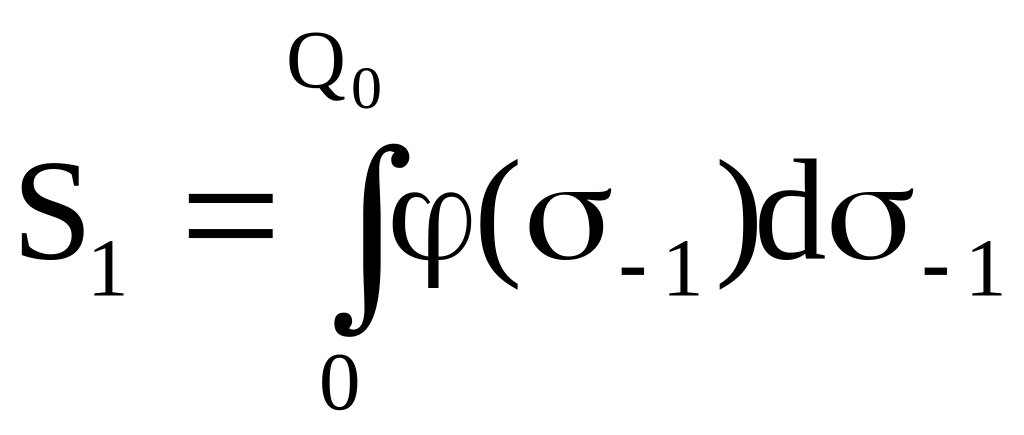Вероятность безотказности рассчитываемой детали:

P>(1-S₁)(1-S₂)

Учитывая, что Р+F=1 , получим:

1-P<S₁+S₂-S₁S₂

Отсюда выражение для оценки точности данного приближенного ме­тода расчета вероятности безотказности рассчитываемой детали:

S₁S₂<1-P<S₁+S₂-S₁S₂

Таким образом, переход при расчетах прочности к использованию вероятностных распределений значений нагрузок и прочности позволяет вести расчеты с обеспечением требуемого уровня безотказности.