Интегральные теплоты растворения солей, образующих кристаллогидраты, при 25 с

Вещество	Число молей H2O на 1 моль соли	–Hm, кДж/моль
BaCl2	400	11,18
BaCl2 H2O	400	–7,74
BaCl2 2H2O	400	–18,74
CuSO4	500	68,37
CuSO4 H2O	500	40,42
CuSO4 3H2O	500	12,68
CuSO4 5H2O	500	–10,50
LiCl	800	36,53
LiCl H2O	800	18,58
LiCl 2H2O	800	4,06
LiCl 3H2O	800	–8,83
MgSO4	400	87,61
MgSO4 2H2O	400	46,36
MgSO4 4H2O	400	17,66
MgSO4 6H2O	400	1,00
MgSO4 7H2O	400	–15,86
Na2CO3	400	23,43
Na2CO3 7H2O	400	–45,86
Na2CO3 10H2O	400	–69,04
Na2HPO4	500	25,94
Na2HPO4 2H2O	500	0,17
Na2HPO4 7H2O	500	–47,95
Na2HPO4 12H2O	500	–96,06
ZnSO4	500	77,28
ZnSO4 H2O	500	42,13
ZnSO4 6H2O	500	–4,31
ZnSO4 7H2O	500	–18,87

Работа № 7 (термодинамика) Изучение химического равновесия в гетерогенной системе

Цель работы

Освоить статический метод исследования химического равновесия; изучить зависимость химического равновесия от температуры; по экспериментальным данным рассчитать тепловой эффект и другие термодинамические характеристики реакции.

Вопросы коллоквиума

1. Химическое равновесие. Условие химического равновесия. Константа равновесия.

2. Закон действующих масс. Термодинамический вывод константы равновесия.

3. Подвижность химического равновесия. Принцип Ле-Шателье. Влияние изменения внешних условий на равновесие.

4. Уравнение изобары химической реакции как количественное выражение смещения равновесия при изменении температуры. Анализ и интегрирование уравнения изобары.

5. Определение теплового эффекта реакции по константам равновесия при различных температурах.

6. Экспериментальные методы определения упругости диссоциации.

Приборы и реактивы

1. Печь трубчатая.

2. Манометр.

3. Милливольтметр.

4. Карбонат кальция.

Методика выполнения работы и ее обоснование

Химическое равновесие в гетерогенных системах рассмотрим на примере реакции диссоциации карбоната кальция.

Процессы диссоциации карбонатов широко распространены в металлургии и химической промышленности (обжиг известняка, разложение известняка в доменной печи, где он используется в качестве флюса, известковое кипение в мартеновской печи и т. д.).

Карбонат кальция, являющийся составной частью мела, известняка, мрамора, диссоциирует по реакции:

CaCO_3(т) = CaO_(т) + CO_2(г).

Эта реакции обратима. Константа равновесия имеет вид:

, (7.1)

где – активности оксида и карбоната кальция;

– фугитивность двуокиси углерода.

Считаем, что активности чистых фаз CaCO_3(т) и CaO_(т) при данной температуре постоянны: = 1 и = 1, и при небольших давлениях . Константа равновесия реакции принимает вид:

, (7.2)

где – равновесное давление или упругость диссоциации карбоната кальция.

Изменение упругости диссоциации с ростом температуры можно показать на основании уравнения изобары реакции:

. (7.3)

С учетом (7.2) уравнение изобары для данной реакции можно записать:

. (7.4)

Для процесса диссоциации ∆H > 0, поэтому упругость диссоциации растет с увеличением температуры.

Изменение упругости диссоциации с ростом температуры показано на рис.2. Кривая делит плоскость диаграммы на две области. В области, лежащей выше равновесной кривой, устойчив карбонат кальция, ниже – оксид кальция. Для области I характерны давления CO₂, большие, чем равновесные.

Используя уравнение изотермы:

, (7.5)

можно определить знак ∆G для процесса в условиях I. Так как фактическое давление CO₂ для всех точек этой области выше равновесного, т.е. , то ∆G > 0. Следовательно, в условиях повышенного по сравнению с равновесным, давления CO₂, возможна обратная реакция – процесс карбонизации: CaO_(т) + CO_2(г) = CaCO_3(т).

Аналогично рассуждая для области II, где , можно заключить, что при давлениях ниже равновесного возможно развитие процесса диссоциации, т.к. ∆G < 0.

Численные значения равновесных , атм при различных температурах могут быть получены из уравнения:

, (7.6)

где – тепловой эффект реакции при данной температуре, Дж/моль;

– изменение энтропии реакции для этой же температуры,

Дж/(моль∙К).

Теоретические значения и можно рассчитать, используя справочные величины (табл. 7.2).

П роинтегрировав уравнение (7.4) в пределах и и соответственно T₁ и T₂ (предполагая постоянство ∆H в данном интервале температур), получим соотношение:

, (7.7)

из которого можно найти величину теплового эффекта реакции в данном температурном интервале:

. (7.8)

Рис.2 Зависимость упругости

диссоциации от температуры

Для измерения упругости диссоциации карбонатов часто используют статический метод. Суть его заключается в непосредственном измерении давления в установке, предварительно откачанной до предельного разряжения. При этом в печи при заданной температуре помещена навеска карбоната кальция. При малых равновесных давлениях измеряют с помощью манометра Мак-Леода, принцип действия которого основан на законе PV = const. При больших упругостях диссоциации иногда ограничиваются масляным U – образным манометром (рис.3).

Рис.3. Схема установки: 1 – образец; 2 – термопара; 3 – милливольтметр; 4 – печь; 5 – кварцевая трубка; 6 – вакуумметр; 7 – двухходовой кран.

Порядок выполнения работы

1. Через открытый конец кварцевой трубки (рис. 3) в печь помещают навеску карбоната кальция, вес которой строго не контролируется, однако должен быть избыток карбоната по сравнению с количеством, необходимым для установления равновесия. Иногда навеска бывает заранее внесена в трубку печи. Конец трубки закрывается шлифом или пробкой и включается масляный ротационный насос. Вакуумный кран при этом открыт, а кран для впуска воздуха закрыт. Если опыт производится с навеской повторно (перед началом опыта в установке разряжение), то вакуумный кран открывают на 2 – 3 минуты после включения насоса, когда в части системы создается разряжение. Открывать вакуумный кран следует очень осторожно, поддерживая его левой рукой, а правой плавно поворачивая пробку крана. Система откачивается до предельного разряжения. Закрывают вакуумный кран, включают насос и открывают кран для впуска воздуха. При использовании только трехходового крана впуск воздуха и подсоединение вакуума производятся с его помощью. Выполняется в присутствии преподавателя.

2. Систему выдерживают под вакуумом, проверяя ее надежность в течение 5 – 10 минут. Затем включают печь и доводят температуру до первой заданной. Поддерживая температуру постоянной в течение 10 – 15 минут, достигают установления постоянного давления, определяемого манометром. Показание манометра при данной температуре позволяет рассчитать упругостью диссоциации известняка. При высоких температурах выдержку можно делать меньше, чем при низких, так как скорость реакции с ростом температуры возрастает. При достижении постоянного давления записывают его величину и повышают температуру печи до следующей заданной. Таким образом, производят измерения разновесных давлений CO₂ при нескольких температурах в диапазоне 500 – 800°С с шагом в 25 – 50°С (по заданию преподавателя).

3. По опытным данным строят график в координатах ln – 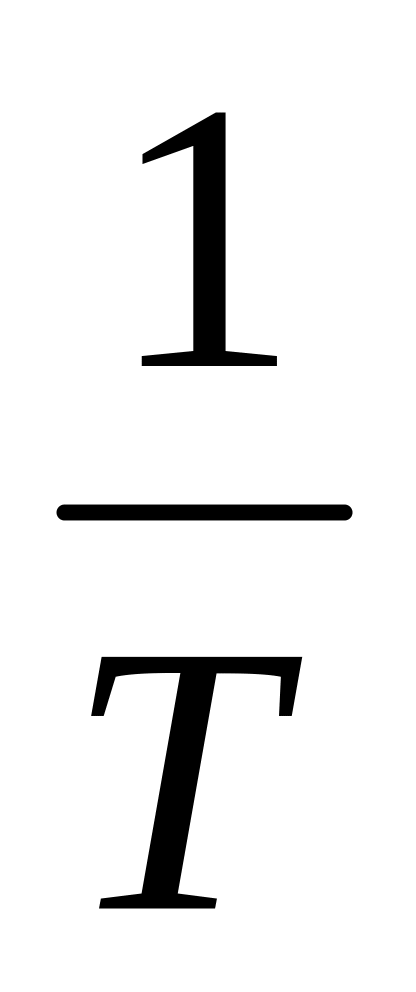, из которого определяют тепловой эффект реакции по уравнению 7.8.

4. Теоретические значения рассчитывают по уравнению 7.6. Величины и находят с помощью справочных данных (табл. 7.2).

5. Сопоставляют теоретические и опытные значения и и делают вывод о влиянии температуры на химическое равновесие.

Таблица 7.1

Опытные и теоретические данные

Опытные данные						Теоретические данные
температура, T		показания вакууметра		ln	, K–1	,	,	ln
°С	K	n	, Па						атм	Па

Таблица 7.2

Справочные термодинамические данные

Вещество	Н0f,298,	S0298,	Коэффициенты уравнения С0P = f (T)
			а	b103	с110–5
СаСО3 (т)	–1206,83	91,71	104,52	21,92	–25,94
СаО (т)	–635,10	38,07	49,63	4,52	–6,95
СО2 (г)	–393,51	213,66	44,14	9,04	–8,53