
- •1.1.1 Цепная реакция деления ядер.
- •Три характерных для ввэр типа кривых температурного эффекта.
- •1.2. Корпус реактора.
- •1.3. Верхний блок реактора.
- •1.4. Детали узла уплотнения главного разъема реактора.
- •1.5. Шахта реактора.
- •1.6. Блок защитных труб (бзт).
- •1.7. Выгородка.
- •1.8. Привод шэм.
- •1.9. Оборудование бетонной шахты реактора.
Типа титульный лист
и оглавление
0 Введение
ВВЭР (Водо-Водяной Энергетический Реактор) — водо-водяной корпусной энергетический ядерный реактор с водой под давлением, одна из наиболее удачных ветвей развития ядерных энергетических установок, получившая широкое распространение в мире.
ВВЭР был разработан в СССР параллельно с реактором РБМК и обязан своим происхождением одной из рассматривающихся в то время реакторных установок для атомных подводных лодок. Идея реактора была предложена в Курчатовском институте С. М. Фейнбергом. Работы над проектом начались в1954 году, в 1955 году ОКБ «Гидропресс» приступило к его разработке. Научное руководство осуществляли И. В. Курчатов и А. П. Александров.
Общее название реакторов этого типа в других странах — PWR, они являются основой мировой мирной ядерной энергетики. Первая станция с таким реактором была запущена в США в 1957 году, АЭС Шиппингпорт.
Первый советский ВВЭР (ВВЭР-210) был введен в эксплуатацию в 1964 году на первом энергоблоке Нововоронежской АЭС. Нововоронежская АЭС-2 - строящаяся станция неподалёку от Нововоронежской АЭС. Станция сооружается по новому проекту АЭС-2006, который предусматривает использование реакторов ВВЭР-1200, в настоящий момент ведётся сооружение 2-х энергоблоков общей мощностью 2400 МВт, в дальнейшем планируется построить ещё 2. Первоначально пуск первого энергоблока был запланирован на конец 2012 года, однако он был перенесён на 2014 год.
1 Физические основы ядерной энергетики
1.1 Ядерный реактор
1.1.1 Цепная реакция деления ядер.
Рассмотрим механизм цепной реакции деления. При делении тяжелых ядер под действием нейтронов возникают новые нейтроны. Например, при каждом делении ядра урана 92U235 в среднем возникает 2.4 нейтрона. Часть этих нейтронов снова может вызвать деление ядер. Такой лавинообразный процесс называется цепной реакцией. Цепная реакция деления идет в среде, в которой происходит процесс размножения нейтронов. Такая среда называется активной зоной. Важнейшей физической величиной, характеризующей интенсивность размножения нейтронов, является коэффициент размножения нейтронов в среде k∞. Коэффициент размножения равен отношению количества нейтронов в одном поколении к их количеству в предыдущем поколении. Индекс ∞ указывает, что речь идет об идеальной среде бесконечных размеров. Аналогично величине k∞ определяется коэффициент размножения нейтронов в физической системе k. Коэффициент k является характеристикой конкретной установки. В делящейся среде конечных размеров часть нейтронов будет уходить из активной зоны наружу. Поэтому коэффициент k зависит еще от вероятности Р для нейтрона не уйти из активной зоны. По определению
k = k∞P. |
(1.1) |
Величина
Р зависит от состава активной зоны, ее
размеров, формы, а также от того, в какой
степени окружающее активную зону
вещество отражает нейтроны.
С возможностью ухода нейтронов за
пределы активной зоны связаны важные
понятия критической массы и критических
размеров. Критическим
размером называется
размер активной зоны, при котором
k = 1. Критической
массой называется
масса активной зоны критических размеров.
Очевидно, что при массе ниже критической
цепная реакция не идет, даже если ![]() > 1.
Наоборот, заметное превышение массы
над критической ведет к неуправляемой
реакции - взрыву.
Если
в первом поколении имеется N нейтронов,
то в n-м поколении их будет Nkn.
Поэтому при k = 1 цепная реакция
идет стационарно, при k < 1 реакция
гаснет, а при k > 1 интенсивность реакции
нарастает. При k = 1 режим реакции
называется критическим,
при k > 1 – надкритическим и
при k < 1 – подкритическим.
Время жизни одного поколения
нейтронов
> 1.
Наоборот, заметное превышение массы
над критической ведет к неуправляемой
реакции - взрыву.
Если
в первом поколении имеется N нейтронов,
то в n-м поколении их будет Nkn.
Поэтому при k = 1 цепная реакция
идет стационарно, при k < 1 реакция
гаснет, а при k > 1 интенсивность реакции
нарастает. При k = 1 режим реакции
называется критическим,
при k > 1 – надкритическим и
при k < 1 – подкритическим.
Время жизни одного поколения
нейтронов ![]() сильно
зависит от свойств среды и имеет порядок
от 10–4 до
10–8 с.
Из-за малости этого времени для
осуществления управляемой цепной
реакции надо с большой точностью
поддерживать равенство k = 1, так
как, скажем, при k = 1.01 система почти
мгновенно взорвется. Посмотрим, какими
факторами определяются коэффициенты
k∞ и
k.
Первой величиной,
определяющей k∞(или
k), является среднее число
сильно
зависит от свойств среды и имеет порядок
от 10–4 до
10–8 с.
Из-за малости этого времени для
осуществления управляемой цепной
реакции надо с большой точностью
поддерживать равенство k = 1, так
как, скажем, при k = 1.01 система почти
мгновенно взорвется. Посмотрим, какими
факторами определяются коэффициенты
k∞ и
k.
Первой величиной,
определяющей k∞(или
k), является среднее число ![]() нейтронов,
испускаемых в одном акте деления.
Число
зависит
от вида горючего и от энергии падающего
нейтрона. В табл. 1 приведены
значения
основных
изотопов ядерной энергетики, как для
тепловых, так и для быстрых (Е = 1 МэВ)
нейтронов.
нейтронов,
испускаемых в одном акте деления.
Число
зависит
от вида горючего и от энергии падающего
нейтрона. В табл. 1 приведены
значения
основных
изотопов ядерной энергетики, как для
тепловых, так и для быстрых (Е = 1 МэВ)
нейтронов.
|
Рис.1. Энергетический спектр нейтронов, испущенных при делении тепловыми нейтронами ядра 235U |
При столкновении нейтрона с тяжелым ядром всегда возможен радиационный захват нейтрона (n,γ). Этот процесс будет конкурировать с делением и тем самым уменьшать коэффициент размножения. Отсюда вытекает, что второй физической величиной, влияющей на коэффициенты k∞, k, является вероятность деления при захвате нейтрона ядром делящегося изотопа. Эта вероятность для моноэнергетических нейтронов, очевидно, равна
|
(1.2) |
где ![]() nf,
nγ –
соответственно сечения деления и
радиационного захвата. Для одновременного
учета как числа нейтронов на акт деления,
так и вероятности радиационного захвата
вводится коэффициентη, равный среднему
числу вторичных нейтронов на один захват
нейтрона делящимся ядром.
nf,
nγ –
соответственно сечения деления и
радиационного захвата. Для одновременного
учета как числа нейтронов на акт деления,
так и вероятности радиационного захвата
вводится коэффициентη, равный среднему
числу вторичных нейтронов на один захват
нейтрона делящимся ядром.
|
(1.3) |
величина η зависит от вида горючего и от энергии нейтронов. Значения η для важнейших изотопов для тепловых и быстрых нейтронов приведены в той же табл. 1. Величина η является важнейшей характеристикой ядер горючего. Цепная реакция может идти только при η > 1. Качество горючего тем выше, чем больше значение η.
Таблица 1. Значения ν, η для делящихся изотопов
Ядро |
92U233 |
92U235 |
94Pu239 |
|
Тепловые нейтроны (Е = 0.025 эВ) |
ν |
2.52 |
2.47 |
2.91 |
η |
2.28 |
2.07 |
2.09 |
|
Быстрые нейтроны (E = 1 МэВ) |
ν |
2.7 |
2.65 |
3.0 |
η |
2.45 |
2.3 |
2.7 |
|
Качество
ядерного горючего определяется его
доступностью и коэффициентом η. В
природе встречаются только, три изотопа,
которые могут служить ядерным топливом
или сырьем для его получения. Это изотоп
тория 232Th
и изотопы урана 238U
и 235U.
Из них первые два цепной реакции не
дают, но могут быть переработаны в
изотопы, на которых реакция идет.
Изотоп 235U
сам дает цепную реакцию. В земной коре
тория в несколько раз больше, чем урана.
Природный торий практически состоит
только из одного изотопа 232Th.
Природный уран в основном состоит из
изотопа238U
и только на 0.7% из изотопа 235U.
На практике крайне важен вопрос об
осуществимости цепной реакции на
естественной смеси изотопов урана, в
которой на одно ядро 235U
приходится 140 ядер 238U.
Покажем, что на естественной смеси
медленная реакция возможна, а быстрая
– нет. Для рассмотрения цепной реакции
на естественной смеси удобно ввести
новую величину – среднее сечение ![]() поглощения
нейтрона, отнесенное к одному ядру
изотопа 235U.
По определению
поглощения
нейтрона, отнесенное к одному ядру
изотопа 235U.
По определению
|
(1.4) |
где верхний индекс указывает массовое число соответствующего изотопа урана. Вероятность того, что нейтрон, поглотившись в естественной смеси, вызовет деление, равна
 .
.
Умножив эту вероятность на число ν нейтронов, вылетающих в среднем при делении одного ядра, мы получим по аналогии с (3) коэффициент ηест для естественной смеси:
|
(1.5) |
Для
тепловых нейтронов
=
2.47, ![]() =
580 барн,
=
580 барн, ![]() =
112 барн,
=
112 барн, ![]() =
2.8 барн (обратите внимание на малость
последнего сечения). Подставив эти цифры
в (5), мы получим, что для медленных
нейтронов в естественной смеси
=
2.8 барн (обратите внимание на малость
последнего сечения). Подставив эти цифры
в (5), мы получим, что для медленных
нейтронов в естественной смеси
|
(1.6) |
Это
означает, что 100 тепловых нейтронов,
поглотившись в естественной смеси,
создадут 132 новых нейтрона. Отсюда прямо
следует, что цепная реакция на медленных
нейтронах в принципе возможна на
естественном уране. В принципе, потому
что для реального осуществления цепной
реакции надо уметь замедлять нейтроны
с малыми потерями.
Для быстрых
нейтронов ν = 2.65,
![]() 2
барн,
0.1
барн. Если учитывать деление только на
изотопе 235U,
получим
2
барн,
0.1
барн. Если учитывать деление только на
изотопе 235U,
получим
235(быстр.) 0.3. |
(1.7) |
Но надо еще учесть, что быстрые нейтроны с энергиями больше 1 МэВ могут с заметной относительной интенсивностью делить и ядра изотопа 238U, которого в естественной смеси очень много.
Для деления на 238U коэффициент равен примерно 2.5. В спектре деления примерно 60% нейтронов имеют энергии выше эффективного порога 1.4 МэВ деления на 238U. Но из этих 60% только один нейтрон из 5 успевает произвести деление, не замедлившись до энергии ниже пороговой за счет упругого и особенно неупругого рассеяния. Отсюда для коэффициента 238(быстр.) получается оценка
η238(быстр.) = 0.6ν238/5 ≈ 0.3. |
(1.8) |
Полный коэффициент ηест для быстрой реакции равен сумме:
ηест(быстр.) = η235(быстр.) + η238(быстр.) ≈ 0.6 < 1. |
(1.9) |
Таким образом, на быстрых нейтронах цепная реакция в естественной смеси (235U + 238U) идти не может. Экспериментально установлено, что для чистого металлического урана коэффициент размножения достигает значения единицы при обогащении 5.56%. Практически оказывается, что реакцию на быстрых нейтронах можно поддерживать лишь в обогащенной смеси, содержащей не меньше 15% изотопа 235U. Естественную смесь изотопов урана можно обогащать изотопом 235U. Обогащение является сложным и дорогостоящим процессом из-за того, что химические свойства обоих изотопов почти одинаковы. Приходится пользоваться небольшими различиями в скоростях химических реакций, диффузии и др., возникающими вследствие различия масс изотопов. Цепную реакцию на 235U практически всегда осуществляют в среде с большим содержанием 238U. Часто используется естественная смесь изотопов, для которой η = 1.32 в области тепловых нейтронов, так как 238U также полезен. Изотоп 238U делится нейтронами с энергией выше 1 МэВ. Это деление приводит к небольшому дополнительному размножению нейтронов. Сравним цепные реакции деления на тепловых и быстрых нейтронах. У тепловых нейтронов сечения захвата велики и сильно меняются при переходе от одного ядра к другому. На ядрах некоторых элементов (например, на кадмии) эти сечения в сотни и более раз превосходят сечения на 235U. Поэтому к активной зоне установок на тепловых нейтронах предъявляются требования высокой чистоты по отношению к некоторым примесям. Для быстрых нейтронов все сечения захвата малы и не так уж сильно отличаются друг от друга, так что проблемы высокой чистоты материалов не возникает. Другим преимуществом быстрых реакций является более высокий коэффициент воспроизводства. Важное отличительное свойство тепловых реакций состоит в том, что в активной зоне топливо значительно сильнее разбавлено, т. е. на одно ядро топлива приходится значительно больше не участвующих в делении ядер, чем в быстрой реакции. Например, в тепловой реакции на естественном уране на ядро топлива 235U приходится 140 ядер сырья 238U, а в быстрой реакции на ядро 235U может приходиться не более пяти-шести ядер 238U. Разбавленность топлива в тепловой реакции приводит к тому, что одна и та же энергия в тепловой реакции выделяется в значительно большем объеме вещества, чем в быстрой. Тем самым из активной зоны тепловой реакции легче отводить тепло, что позволяет осуществлять эту реакцию с большей интенсивностью, чем быструю. Время жизни одного поколения нейтронов для быстрой реакции на несколько порядков меньше, чем для тепловой. Поэтому скорость протекания быстрой реакции может заметно измениться через очень короткое время после изменения физических условий в активной зоне. При нормальной работе реактора этот эффект несуществен, поскольку в этом случае режим работы определяется временами жизни запаздывающих, а не мгновенных нейтронов. В однородной среде, состоящей только из делящихся изотопов одного вида, коэффициент размножения был бы равен η. Однако в реальных ситуациях, кроме делящихся ядер, всегда присутствуют другие, неделящиеся. Эти посторонние ядра будут захватывать нейтроны и тем самым влиять на коэффициент размножения. Отсюда следует, что третьей величиной, определяющей коэффициенты k∞, k, является вероятность того, что нейтрон не будет захвачен одним из неделящихся ядер. В реальных установках “посторонний” захват идет на ядрах замедлителя, на ядрах различных конструктивных элементов, а также на ядрах продуктов деления и продуктов захвата. Для осуществления цепной реакции на медленных нейтронах в активную зону вводят специальные вещества – замедлители, которые превращают нейтроны деления в тепловые. На практике цепная реакция на медленных нейтронах осуществляется на естественном или слегка обогащенном изотопом235U уране. Присутствие большого количества изотопа 238U в активной зоне усложняет процесс замедления и делает необходимым предъявление высоких требований к качеству замедлителя. Жизнь одного поколения нейтронов в активной зоне с замедлителем приближенно можно разбить на две стадии: замедление до тепловых энергий и диффузия с. тепловыми скоростями до поглощения. Для того чтобы основная часть нейтронов успела замедлиться без поглощения, необходимо выполнение условия
σупр/σзахв >> n, |
(1.10) |
|
|
Замедляющие свойства активной среды приближенно могут быть описаны тремя величинами: вероятностью нейтрону избежать поглощения замедлителем во время замедления, вероятностью р избежать резонансного захвата ядрами 238U и вероятностью f тепловому нейтрону поглотиться ядром горючего, а не замедлителя. Величина f называется обычно коэффициентом теплового использования. Точный расчет этих величин сложен. Обычно для их вычисления пользуются приближенными полуэмпирическими формулами.
Величины p и f зависят не только от относительного количества замедлителя, но и от геометрии его размещения в активной зоне. Активная зона, состоящая из однородной смеси урана и замедлителя, называется гомогенной, а система их чередующихся блоков урана и замедлителя называется гетерогенной. Качественно гетерогенная система отличается тем, что в ней образовавшийся в уране быстрый нейтрон успевает уйти в замедлитель, не достигнув резонансных энергий. Дальнейшее замедление идет уже в чистом замедлителе. Это повышает вероятность p избежать резонансного захвата
pгет > pгом.
С другой стороны, наоборот, став в замедлителе тепловым, нейтрон должен для участия в цепной реакции продиффундировать, не поглотившись в чистом замедлителе, до его границы. Поэтому коэффициент теплового использования f в гетерогенной среде ниже, чем в гомогенной:
fгет < fгом.
Для оценки коэффициента размножения k∞ теплового реактора используется приближенная формула четырех сомножителей
k∞ = ηpfε. |
(1.11) |
Первые три сомножителя мы уже рассматривали ранее. Величина ε называется коэффициентом размножения на быстрых нейтронах. Этот коэффициент вводится для того, чтобы учесть, что часть быстрых нейтронов может произвести деление, не успев замедлиться. По своему смыслу коэффициент ε всегда превышает единицу. Но это превышение обычно невелико. Типичным для тепловых реакций является значение ε = 1.03. Для быстрых реакций формула четырех сомножителей неприменима, так как каждый коэффициент зависит от энергии и разброс по энергиям при быстрых реакциях очень велик. Поскольку величина η определяется видом топлива, а величина ε для медленных реакций почти не отличается от единицы, то качество конкретной активной среды определяется произведением pf. Так, преимущество гетерогенной среды перед гомогенной количественно проявляется в том, что, например, в системе, в которой на одно ядро естественного урана приходится 215 ядер графита, произведение pf равно 0,823 для гетерогенной среды и 0,595 для гомогенной. А так как для естественной смеси η = 1,34, то мы и получим, что для гетерогенной среды k∞ > 1, а для гомогенной k∞ < 1. Для практического осуществления стационарно текущей цепной реакции надо уметь этой реакцией управлять. Это управление существенно упрощается благодаря вылету запаздывающих нейтронов при делении. Подавляющее большинство нейтронов вылетает из ядра практически мгновенно (т. е. за время, на много порядков меньшее времени жизни поколения нейтронов в активной зоне), но несколько десятых процента нейтронов являются запаздывающими и вылетают из ядер-осколков через довольно большой промежуток времени – от долей секунды до нескольких и даже десятков секунд. Качественно влияние запаздывающих нейтронов можно пояснить так. Пусть коэффициент размножения мгновенно возрос от подкритического значения до такого надкритического, что k < 1 при отсутствии запаздывающих нейтронов. Тогда, очевидно, цепная реакция начнется не сразу, а лишь после вылета запаздывающих нейтронов. Тем самым процесс течения реакции будет регулируемым, если время срабатывания регулирующих устройств будет меньше сравнительно большого времени задержки запаздывающих нейтронов, а не очень малого времени развития цепной реакции. Доля запаздывающих нейтронов в ядерных горючих колеблется от 0.2 до 0.7%. Среднее время жизни запаздывающих нейтронов составляет приблизительно 10 с. При небольшой степени надкритичности скорость нарастания интенсивности цепной реакции определяется только запаздывающими нейтронами. Захват нейтронов не участвующими в цепной реакции ядрами снижает интенсивность реакции, но может быть полезным в отношении образования новых делящихся изотопов. Так, при поглощении нейтронов изотопов урана 238U и тория 232Th образуются (через два последовательных b-распада) изотопы плутония 239Pu и урана 233U, являющиеся ядерным горючим:
|
(1.12) |
|
(1.13) |
Эти две реакции открывают реальную возможность воспроизводства ядерного горючего в процессе течения цепной реакции. В идеальном случае, т. е. при отсутствии ненужных потерь нейтронов, на воспроизводство может идти в среднем – 1 нейтронов на каждый акт поглощения нейтрона ядром горючего.
Зависимость эффективного коэффициента размножения от обогащения ядерного топлива.
На рис. 2.3 показана зависимость k∞ от обогащения (2.11). Видно, что при увеличении e5 от 0,712% до 5% значение k∞ возрастает от 1,0 до 1,42, хотя темп роста постепенно падает.
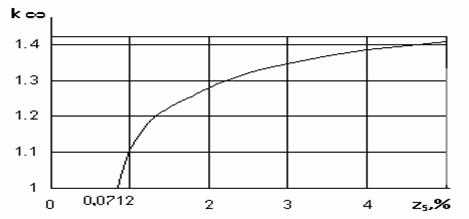
Рис.2.3 Зависимость эффективного коэффициента размножения от обогащения ядерного топлива
Условия критичности реактора.
Итак, выше были определены способы оценки коэффициентов размножения для бесконечной среды k∞ , теперь необходимо связать свойства реального реактора конечных размеров и состава среды и указать условия критичности для него.
Для этого для реактора на тепловых нейтронах в модели диффузии необходимо ввести ряд понятий.
Материальный параметр реактора c2м определяется как величина:
c2м =1/L2*(nfSf /Sа –1) (2.13)
Геометрический параметр реактора В20 (или баклинг) в наиболее распространенном случае цилиндрического реактора определяется как :
В20=(2.405/R)2+(p/H)2 (2.14)
Где: R – радиус, а Н – высота реактора, соответственно.
Следует отметить, что в состав c2м входят только характеристики материального состава реактора (диффузионные, поглощающие и т.п.). В состав В20 входят напротив только характеристики размеров реактора.
Условие критичности реактора без отражателя формулируется (без доказательств) следующим образом:
«Необходимым и достаточным условием критичности для реактора без отражателя (только для тепловых нейтронов в диффузионном приближении) является равенство материального и геометрического параметров» т.е. :
c2м = В20. (2.15а)
Другой формой этого же условия является уже известное нам соотношение:
Kэфф = k∞ *Р (2.15в)
Где Р- вероятность избежать утечки в диффузионном приближении. Эта вероятность может быть записана как:
Р=1/(1+ L2 *В02)
Тогда выражение для Kэфф приобретает самый известный вид:
Kэфф = k∞ */(1+ L2 *В02) (2.15с)
Практическая важность этих условий состоит в том, что они указывают пути вывода реактора в критическое состояние. В соответствии с (2.15а) реактор можно вывести в критическое состояние (а потом удерживать в нем) только двумя путями:
При фиксированном составе среды ( обогащении топлива и поглощении) реактор можно сделать критическим путем изменения размера размножающей среды (т.е. В02 ). Это можно реализовать догрузкой топливных кассет, изменением уровня воды в решетке топливных элементов и т.п.
При фиксированном размере реактор можно вывести в критическое состояние (а потом удерживать в нем) изменением состава среды – т.е. загрузкой свежего топлива и выгрузкой выгоревшего (изменение обогащение топлива) или введением/извлечением поглотителей ( т.е. изменением c2м ) .
Реально можно использовать оба пути, но в реакторах ВВЭР изменение поглощения обычно регулируется с помощью борной кислоты или стержней системы управления, а изменение свойств деления –загрузкой свежего топлива.
Указанные соотношения получены аналитически, но в них учтены вклады только тепловых диффундирующих нейтронов.
Если в рассмотрении учесть также замедляющиеся нейтроны, то оценки будут точнее. Для замедляющихся нейтронов вводится понятие «возраст нейтронов»:
t(u)=  (2.16)
(2.16)
где u- летаргия нейтронов (u=ln(2МэВ/Е) ). Вводится характеристика, объединяющая характеристики замедления и диффузии, называемая «площадью миграции» - М2= L2 +t.
Тогда более точной и наиболее употребляемой оценкой для Кэф, аналогичной (2.15c), будет :
Кэф = k∞ */(1+ М2 *В02) (2.15d)
Наконец, последнее уточнение этих соотношений необходимо, если в реакторе используется отражатель толщиной D. Тогда в геометрическом параметре вместо радиуса R и высоты реактора Н используется (R+d) и (Н+d), где d -т.н. эффективная добавка отражателя d.Реакторы на ториевом топливном цикле подобны реакторам на быстрых нейтронах. В реакторах этого типа естественный торий-232 при поглощении нейтронов превращается в делящийся изотоп урана (уран-233). Этот изотоп, участвуя в цепной реакции деления, выделяет теплоту и избыточные нейтроны, которые преобразовывают еще большее количество тория в U-233. Такая технология привлекательна тем, что, во-первых, позволяет избежать производства плутония, во-вторых, в качестве топлива используется довольно распространенный торий, а, в-третьих, эффективность использования топлива может быть близка к эффективности реакторов на быстрых нейтронах.
Характеристики поля нейтронов
Плотность нейтронов (n). Попросту говоря, это число нейтронов, находящихся в данный момент времени в единичном объёме среды. Из этого определения следует, что размерность плотности нейтронов - нейтр./см3, или формально - см-3. Плотность нейтронов является сугубо статической характеристикой: в определении нет и намёка на то, что нейтроны движутся; в нём внимание сосредоточено только на факте присутствия в данный момент времени в единичном объёме среды определённого числа нейтронов, фиксации их в этом единичном объёме подобно тому, как моментальная фотография фиксирует положение множества движущихся объектов, попадающих в поле зрения объектива, не давая при этом представления ни о характере, ни о направлении, ни о скорости их движения. Благостная простота этого определения, давая легко воспринимаемое представление о плотности нейтронов, имеет один изъян: представляя факт присутствия n нейтронов в единичном объёме среды, оно не даёт представления о том, равномерно или неравномерно размещены эти нейтроны в этом объёме. По существу, это простое выражение является определением средней величины плотности нейтронов. Для математического описания больших количеств нейтронов в больших объёмах среды с помощью непрерывных функций необходимо иметь строгое определение, охватывающее понятие и локальной плотности нейтронов. Вот почему Ядерный Стандарт рекомендует более общее определение: Плотность нейтронов - это отношение числа нейтронов, находящихся в данный момент времени в объёме элементарной сферы, к величине объёма этой сферы. Элементарный объём - это объём, величина которого может быть сколь угодно малой, поэтому (в соответствии с понятием математики) оправданным является его обозначение как dV. Значит, если в объёме dV в данный момент времени содержится dN нейтронов, то локальная плотность нейтронов в этом элементарном объёме (практически - "в точке", т.к. в пределе элементарный объём стягивается в точку) будет:
n = dN/dV . (2.3.1)
Cтандартное определение плотности нейтронов, преодолевая отмеченный изъян простейшего определения, тем самым делает в нашем представлении величину n (изначально дискретную) величиной непрерывной, меняющейся в объёме среды плавно, "от точки к точке", допуская при этом, что n может принимать не только целые значения, но и дробно-долевые, например, n = 0.0784 нейтр/см3 или n = 3.496 нейтр/см3. А это удобно тем, что для математического описания нейтронных полей становится возможным использовать компактный аналитический аппарат непрерывных функций, который во всех отношениях удобнее дискретных описаний.
2.3.2. Скорость движения нейтронов (v) или их кинетическая энергия (Е). В ядерном реакторе функционируют свободные нейтроны широкого диапазона кинетических энергий - от 10-3 эВ до десятков МэВ. Для удобства их различий они классифицируются на: - быстрые нейтроны (с кинетическими энергиями выше 0.1 МэВ); - промежуточные нейтроны (с энергиями 0.625эВ < E < 0.1МэВ); - медленные нейтроны (с энергиями ниже 0.625 эВ). Необходимость такой классификации обусловлена тем, что нейтроны различных кинетических энергий обладают различной склонностью к вступлению в одни и те же нейтронные реакции с ядрами одних веществ. Особую часть медленных нейтронов составляют тепловые нейтроны - то есть нейтроны, находящиеся в кинетическом равновесии с ядрами среды, в которой они движутся. Поскольку энергетическое распределение молекул (а следовательно, и атомов, и ядер атомов) в их тепловом движении имеет вид спектра Л.Больцмана:
N(E) = Nо .C .E exp(-E / kT),
- аналогичное распределение должны иметь в непоглощающей среде и тепловые нейтроны: раз они находятся в кинетическом равновесии с ядрами атомов среды, то каждой группе ядер, имеющих определенную энергию Е, должна соответствовать пропорциональная по численности группа нейтронов той же энергии. Поэтому энергетический спектр тепловых нейтронов – спектр Максвелла - в непоглощающих средах формально описывается тем же выражением:
n(E) = no C E exp(-E / kT) (2.3.3)
где: n(E) - плотность тепловых нейтронов, имеющих энергии в элементарном интервале dE вблизи значения Е; no - интегральная плотность тепловых нейтронов всех возможных энергий в среде с термодинамической температурой Т; k = 8.62 .10-5 эВ/К - постоянная Больцмана; С - постоянный сомножитель нормировки. В реальной (поглощающей нейтроны) среде максвелловское распределение тепловых нейтронов по энергиям, конечно, нарушается. Однако, компактное математическое удобство этого выражения настолько велико, что условились считать, что и в поглощающей тепловые нейтроны среде энергетическое распределение тепловых нейтронов сохраняет ту же (гауссову) форму, что и в непоглощающей среде:
n(E) = no C E exp(-E / kTн), (2.3.4)
с той лишь разницей, что в показателе экспоненциала стоит не термодинамическая температура среды Т, а так называемая температура нейтронов Тн. Максвелловский спектр тепловых нейтронов (рис.2.9) характеризуется следующими присущими ему энергиями тепловых нейтронов: а) Наиболее вероятной энергией Енв = kTн, соответствующей максимуму распределения тепловых нейтронов по энергиям при данной температуре нейтронов Тн. Это означает, что тепловых нейтронов с кинетической энергией Енв в среде больше, чем тепловых нейтронов любых других энергий (до 36% от общего числа всех тепловых нейтронов). б) Средней энергией тепловых нейтронов:
Еср = (1/no) ∫0∞E n(E) dE (2.3.5)
Подстановка в (2.3.5) выражения (2.3.4) приводит к величине:
Eср = 4kTн / p ≈ 1.273 kTн = 1.273 Енв (2.3.6)
В частности при температуре нейтронов Тн = 293К (или 20оС), называемой стандартной температурой, наиболее вероятная и средняя энергии тепловых нейтронов соответственно равны: Eнв = 0.0253 эВ
Еср = 0.0322 эВ Заметим одно замечательное свойство максвелловского спектра: Отношение средней и наиболее вероятной энергий нейтронов в спектре Максвелла при постоянной температуре нейтронов есть величина постоянная, равная Еср/Енв = 4/π ≈ 1.273. Cледовательно, отношение скоростей нейтронов, соответствующих средней и наиболее вероятной энергиям тепловых нейтронов:
vср/vнв = √4/π = 2/√π ≈ 1.128, (2.3.7)
- то есть также является постоянной величиной. Запомним это. Понятие средней энергии тепловых нейтронов понадобилось нам для того, чтобы поведение и взаимодействия всей совокупности различных по энергиям тепловых нейтронов заменить эквивалентным их взаимодействием с ядрами среды так, словно все они одинаковы по энергиям, а значит - и по своим свойствам. Суммирование кинетической энергии всех тепловых нейтронов и раздел этой суммы поровну между всеми тепловыми нейтронами - см. формулу (2.3.5) - как раз и приводит к понятию "среднего теплового нейтрона", подобно понятию "среднего нейтрона деления", с которым мы уже имели дело, говоря о спектре Уатта. Итак, спектр нейтронов, то есть их энергетическое распределение в среде, является второй характеристикой нейтронного поля. К сожалению, теория реакторов до сих пор не располагает компактным аналитическим выражением для спектра всех нейтронов в реакторе, и поэтому задачу по выяснению реакторного спектра приходится решать путём громоздких вычислений с помощью ЭВМ. Частные же задачи теории решаются на базе трёх энергетических спектров: спектр нейтронов деления (Уатта); спектр тепловых нейтронов (Максвелла) и спектр замедляющихся нейтронов (Ферми), с которым мы познакомимся позже.
2.3.3. Плотность потока нейтронов. Третья из основных характеристик нейтронных полей - плотность потока нейтронов(Ф) - является попросту произведением первых двух: плотности нейтронов на их скорость:
Ф = n . v (2.3.8)
По физическому смыслу эта величина - суммарный секундный путь всех нейтронов в 1 см3 среды. Однако размерность плотности потока - нейтр/см2 с - может привести к путанице в попытках обнаружить физический смысл этой величины в самой размерности: сразу воображается некая плоская площадка размером в 1 см2, через которую ежесекундно проходит определённое число нейтронов. Такому представлению способствует прошлый опыт изучения сходным образом звучащих величин иной физической природы: плотности потока жидкости (из гидродинамики), плотности магнитного потока и плотности потока электронов в проводнике (из электродинамики), плотности теплового потока на теплоотдающей поверхности (из теплотехники) и другими. Аналогия плотности потока нейтронов с перечисленными величинами несостоятельна, так как все эти величины характеризуют направленный перенос энергии, а нейтроны в единичном объёме среды движутся не направленно, а хаотично по всем возможным направлениям. На первый взгляд эта характеристика вообще кажется лишней, т.к. она - простая комбинация двух других характеристик нейтронных полей - плотности (n) и скорости (v) нейтронов. Однако, самое простое рассуждение о том, что секундное количество актов любой нейтронной реакции в 1 см3 среды должно быть прямо пропорционально величинам и плотности нейтронов (n), и скорости их переноса (v), а, следовательно, - величине плотности потока нейтронов (Ф), даёт этой характеристике право на существование. Действительно, чем больше плотность нейтронов n и чем больше скорость их перемещения v, тем больше шансов имеют все эти нейтроны в 1см3 среды провзаимодействовать с ядрами среды в течение 1 с и вызвать те или иные нейтронные реакции.
В этих рассуждениях, как видим, не содержится ни малейшего намёка на привязку к какому-либо конкретному направлению движения нейтронов в единичном объёме среды. Но зададим себе вопрос: а важно ли вообще направление, по которому нейтрон перед взаимодействием приближается к ядру, если разговор в конечном счёте сводится к ответу на другой вопрос: произойдет ядерное взаимодействие или не произойдет? - Ведь нас в конце концов интересует секундное количество конкретных взаимодействий каждого вида в единичном объёме среды. И если нам не известно о какой-либо анизотропии свойств ядер по отношению к взаимодействующим с ними с разных направлений нейтронам, то проще предположить, что ядру безразлично, ударит ли его нейтрон "в лоб" или "по затылку", - результат должен быть одинаковы. А это значит, что для удовлетворения нашего интереса, касающегося только скоростей нейтронных реакций, нам достаточно скалярной характеристики нейтронного поля (каковой Ф и является).
Выравнивание тепловыделения в активной зоне реактора
Из рассмотрения реакторов с однородной активной зоной и отражателем следует, что существует значительная неравномерность в распределении потока нейтронов (энерговыделения) по объему реактора. Так, в цилиндрической активной зоне реактора максимальная тепловая нагрузка превышает среднюю более чем в 3 раза. Поэтому необходимо применять какие-либо меры по выравниванию нейтронного потока, чтобы уменьшить коэффициенты неравномерности. Известно большое число способов уменьшения неравномерности энерговыделения в современных энергетических реакторах. Все они сводятся к выравниванию числа актов деления ядер топлива по объему активной зоны (физическое профилирование). Поскольку в реакторах на тепловых нейтронах
(*)
то добиться требуемого выравнивания можно либо чисто внешними средствами (например, рабочими органами СУЗ, выгорающими поглотителями и т. д.), либо изменяя концентрацию ядерного топлива по объему реактора. В современных реакторах чаще используют второй способ как наиболее эффективный.
Из формулы (*) следует, что распределение удельного тепловыделения по объему активной зоны определяется распределениями N5(r) — концентрации ядер 235U и плотности потока тепловых нейтронов Фт(r) по объему активной зоны. Величина Ef в является физической константой, Σf5 хоть и зависит от спектра нейтронов (он может изменяться по объему реактора), но σf5 можно тоже считать константой. Поэтому для выравнивания тепловыделения используются способы, основанные на изменении распределения N5(r) и Фт(r) по объему активной зоны. К этим способам относятся:
1) применение эффективных отражателей нейтронов, расположенных вокруг активной зоны,позволяющих уменьшить утечку нейтронов и тем самым выровнять распределение плотности потока тепловых нейтронов и соответственно тепловыделение;
2) создание многозонных реакторов, в которых распределение ядер 235U по радиусу активной зоны выполнено таким образом, чтобы изменение концентрации N5 было примерно обратно пропорционально изменению Фт;
3) применение твердых и жидких поглотителей, изготовленных из материалов, сильно поглощающих тепловые нейтроны. Поглотитель стремятся располагать по радиусу и высоте активной зоны таким образом, чтобы его концентрация была прямо пропорциональна Фт.
Рассмотрим выравнивание энерговыделения с помощью распределения топлива. Наиболее просто это можно осуществить по радиусу реактора.
Качественные распределения потока тепловых нейтронов и ядерной плотности 235U, соответствующие достижению идеального физического профилирования по радиусу реактора [q(r) = const], показаны на рисунке.
Однако добиться на практике физического профилирования энергетических реакторов с помощью непрерывного изменения концентрации делящегося вещества весьма трудно по технологическим и конструктивным причинам.
В связи с этим возникает задача о зонном профилировании активной зоны, при котором концентрация делящегося вещества меняется скачком от зоны к зоне, оставаясь практически постоянной внутри каждой из них. Число зон и их размеры зависят в основном от принятого режима перегрузки. Обычно на практике ограничиваются двумя зонами: центральной и периферийной. Распределение энерговыделения и ядерной плотности 235U по радиусу в случае двухзонного реактора имеют вид, представленный на рисунке.
Зонная компоновка активной зоны принята, например, в корпусных ядерных энергетических реакторах с обычной водой в качестве замедлителя и теплоносителя (ВВЭР), где свежее топливо, т. е. более обогащенное, располагается в периферийной зоне, а выгоревшее, т. е. менее обогащенное, находится в центральной зоне.
Действие отражателя основано на том, что покидающие активную зону нейтроны попадают в окружающую среду и находятся в ней в хаотическом движении, так же как в самой активной зоне. Поэтому часть нейтронов, отражаясь от ядер среды, может возвратиться обратно. Отсюда результирующая утечка нейтронов из активной зоны уменьшается. Отношение числа нейтронов, возвращающихся в активную зону в результате отражения, к числу попадающих в отражатель нейтронов называют коэффициентом внутреннего отражателя нейтронов или альбедо β.
В ядерных реакторах на тепловых и промежуточных нейтронах в качестве отражателей используются вещества, хорошо замедляющие и слабо поглощающие нейтроны, т. е. вещества-замедлители нейтронов. Они обладают самыми высокими альбедо; например, у слоя обычной воды толщиной 2L, где L — длина диффузии тепловых нейтронов, β=0,8, у слоя бериллия той же толщины β=0,9, у графита β=0,94 и утяжелой воды β=0,98.
При этом в отражателе помимо отражения собственно тепловых нейтронов в активную зону происходит замедление быстрых нейтронов, причем более эффективно, чем в самой активной зоне, где имеется определенная вероятность захвата нейтронов. Часть замедлившихся нейтронов возвращается в активную зону и еще больше повышает плотность потока тепловых нейтронов Фт(r) вблизи отражателя. Типичное распределение Фт(r) при наличии отражателя и без него показано на рисунке.
Видно существенное выравнивание Фт(r) в активной зоне за счет отражателя. Влияние отражателя, грубо говоря, сводится к уменьшению утечки нейтронов из активной зоны и соответственно к уменьшению критических размеров реактора. Для геометрического параметра Bg2 это уменьшение учитывается так называемой эффективной добавкой Δ, которая примерно равна длине линейной экстраполяции δ.
В энергетических ядерных реакторах на тепловых нейтронах замедлитель и отражатель обычно выполняются из одного материала. У таких реакторов значение δ зависит от толщины отражателя Т и отношения (τ/L)otp.
Влияние толщины отражателя на значение Δ проявляется из-за того, что слои отражателя, находящиеся на различных расстояниях от активной зоны, отражают нейтроны по-разному. Наиболее эффективными отражателями являются слои, расположенные вблизи активной зоны. С увеличением расстояния от границы активной зоны эффективность отражения нейтронов падает, так как уменьшается доля нейтронов, попадающих в удаленные слои отражателя. Поэтому оказывается, что эффективность слоя отражателя толщиной Т≈1,5М [где М — длина миграции в отражателе] близка к эффективности слоя бесконечной толщины, и дальнейшее увеличение толщины отражателя бесполезно. Для графита предельная толщина составляет около 90 см, для обычной воды — приблизительно 10 см. При оценке отражателей толщиной, равной или большей 1,5М, можно принять, что эффективная добавка равна длине миграции в матерале отражателя (Δ≈М). Тогда для отражателя из графита Δ=60 см, а из обычной воды Δ=6 см (более точные оценки дают 7 см).
Для каждого замедляющего вещества существует предельная толщина отражателя, превышение которой практически не сказывается на распределении потока тепловых нейтронов в активной зоне. Эта предельная толщина отражателя составляет:
для тяжелой воды.......80 см
графита..........120 см
Природная вода из-за сильного поглощения ею нейтронов не годится в качестве отражателя. Если толщина отражателя меньше 30% предельных значений, то эффективные добавки следует принимать равными толщине отражателя. При отражателе предельной толщины эффективные добавки можно принимать равными 50% толщины отражателя. Для промежуточных значений толщины отражателя эффективные добавки можно находить линейной интерполяцией.
Однако в энергетических реакторах Δ<<min(R,H), поэтому коэффициенты мало отличаются от коэффициентов неравномерности для реакторов без отражателя. В небольших реакторах, когда величина Δ соизмерима с R и H, влияние отражателя на коэффициенты неравномерности существенно. Например для водо-водяного реактора с размерами активной зоны Н=2R=1м при Δ=0,1 м значение kz уменьшается от 1,57 до 1,35, kr—от 2,32 до 1,74 иkv=krkz — от 3,64 до 2,34 (т. е. в 1,5 раза). Тогда получается, что без изменения размеров активной зоны использование отражателя позволяет увеличить мощность реактора в 1,5 раза. При этом существенно выравнивается энерговыделение по объему активной зоны.
В ядерных реакторах на быстрых нейтронах вещества-замедлители отсутствуют и в качестве материала отражателей используются тяжелые нуклиды238U или 232Th, которые кроме отражения быстрых нейтронов в основном служат для воспроизводства новых делящихся нуклидов. Эти нуклиды получаются при поглощении ядрами 238U или 232Th вылетевших из активной зоны нейтронов. Поэтому зоны где находятся эти материалы, принято называть не отражателями, а зонами воспроизводства.
В современных энергетических реакторах одновременно применяются все перечисленные выше способы выравнивания тепловыделения. В результате достигаются следующие значения коэффициентов неравномерности: по радиусу 1,2-1,5; по высоте kz= 1,3-1,5; по объему 1,5‑2,5. Например, в реакторе типа ВВЭР это дало возможность снизить коэффициент kv в 2 раза: с 4,8 (реактор ВВЭР-210 на I блоке Нововоронежской АЭС) до 2,4 (реактор серийный ВВЭР-440).
В процессе работы реактора происходит выгорание топлива и поглотителя, соответственно изменяется распределение тепловыделения по активной зоне. Поэтому проводится изменение распределения поглотителей во времени таким образом, чтобы обеспечить минимизацию рассмотренных коэффициентов неравномерности.
Кампания ядерного реактора
Кампания ядерного реактора — время работы реактора с одной и той же загрузкой ядерного топлива.
Когда весь запас реактивности реактора исчерпан, то есть когда компенсирующие стержни заняли свое предельное конечное положение, цепная реакция сама собой прекращается. Она может быть возобновлена только после замены урана в активной зоне. Разумеется, что величину кампании энергетического реактора желательно иметь возможно большей, поскольку получаемая энергия тем дешевле, чем больше её производится при одной загрузке урана. Однако продолжительность кампании ограничена некоторым минимальным значением критической массы. Часть делящегося материала, составляющая эту критическую массу в конце кампании, из-за прекращения цепной реакции делению не подвергается, выгружается из реактора и в дальнейшем может быть использована только после надлежащей переработки урана, если такая переработка оправдана.
Реакторы на естественном уране имеют малый начальный запас реактивности и их кампании обычно определяются этим запасом. В реакторах с обогащённым ураном запас реактивности может быть сделан большим. Однако имеется ещё одно ограничение продолжительности кампании реактора, связанное с реакцией материала тепловыделяющих элементов на накопление продуктов деления. В результате деления ядра вместо одного атома образуются два новых, суммарный объём которых примерно в 2 раза больше объёма разделившегося атома, поскольку все атомы имеют примерно одинаковые объёмы. Помимо этого, новые атомы не могут помещаться в узлах кристаллической решётки урана и размещаются в решётке произвольно. Наконец, существенно, что значительная часть продуктов деления — газы. В результате накопление продуктов деления сопровождается появлением внутренних перенапряжений в материале, повышением давления газа, что в конце концов приводит к образованию трещин, вздутий и деформации тепловыделяющих элементов. Срок службы основного оборудования реактора много больше, чем урановых элементов, и последние по завершении кампании должны выгружаться из активной зоны. Однако эта операция становится невозможной в случае их деформации. Кроме того, у повреждённых ТВЭЛов нарушается герметичность покрытия, и радиоактивные газы проникают в теплоноситель. Все это означает, что срок службы урановых блоков в ядерном реакторе должен определяться их стойкостью по отношению к разрушительному воздействию накапливающихся продуктов деления. Соответственно, кампания реактора должна определяться, прежде всего, указанной стойкостью тепловыделяющих блоков, а начальный запас реактивности должен быть таким, чтобы он полностью истощался к концу срока пребывания урановых блоков в реакторе. В противном случае по окончании кампании из реактора будет выгружаться лишнее количество неиспользованного делящегося материала, что невыгодно.
Накопление продуктов деления характеризуется их количеством в граммах, приходящимся на тонну урана. Однако непосредственное измерение массы продуктов деления крайне сложно. Зато всегда известно полное количество энергии, выделившейся в активной зоне реактора при делении. Поскольку же деление 1 г урана сопровождается освобождением примерно 1 МВт·сутки тепловой энергии и образованием около 1 г продуктов деления, то число выработанных мегаватт-суток тепловой энергии приблизительно равно числу граммов продуктов деления. Полная масса загруженного в реактор урана также известна. Поэтому количество накопившихся продуктов деления выражают в единицах МВт·сутки/т — количеством мегаватт-суток на тонну урана.
Каждый материал характеризуется своим пределом по накоплению продуктов деления — допустимой глубиной выгорания делящихся атомов. Глубина выгорания для металлического урана составляет 3000—3500 МВт·сутки/т, но для его соединений может быть много больше. Например, оксид урана является веществом пористым и поэтому способным накопить много больше, чем металлический уран, продуктов деления без видимых нарушений формы тепловыделяющего элемента — до 20 000 МВт·сутки/т, а возможно, и больше — до 100 000 МВт·сутки/т. Тонна естественного урана содержит около 7 кг 235U. Глубина выгорания 3500 МВт·сутки/т соответствует делению 3,5 кг атомов. Однако не все продукты деления происходят от 235U, ведь в реакторе накапливается 239Pu, который также участвует в делении. Поэтому часть продуктов деления получается из плутония, и 235U расходуется меньше, чем получается продуктов деления. Чем выше допустимая глубина выгорания, тем больше длительность кампании реактора и тем экономичнее ядерная энергетическая установка с заданным топливом. Однако большие глубины выгорания предполагают обогащённый уран, который намного дороже естественного. Минимальная критическая масса в конце кампании меньше в том случае, если топливом является металлический уран, а не его соединения, например, с кислородом. Поэтому экономичность применения того или иного вида ядерного топлива определяется многими факторами.
Температурные эффекты в реакторе
Температурным эффектом реактивности реактора при рассматриваемой средней температуре теплоносителя в активной зоне называется ве- личина изменения реактивности при его разогреве от 20оС до этой температуры. Из определения сразу следует, что величина температурного эффекта реактивности при температуре 20оС равна нулю. Этой условностью договорились определить начало отсчета величины температурного эффекта.Поскольку в определении идёт речь об изменении реактивности, величина температурного эффекта (как и всякая реактивность) обозначается символом ρt c нижним индексом "t", позволяющим отличать температурный эффект от реактивности любого другого происхождения. Почему ρt, а не Δρt, т.к. в определении речь идет об изменении реактивности? - Именно потому, что ρt(20oC) = 0.
Поскольку из определения можно понять, что величина температурного эффекта - изменяющаяся с температурой величина, нелишне указать в обозначении, какой температуре соответствует данный температурный эффект реактивности, - то есть полное обозначение ТЭР, исключающее какую-либо неопределённость толкования этой величины, должно быть ρt(t). Поэтому и изменение реактивности при разогреве реактора от 20о до произвольной средней температуры теплоносителя t будет равно: Δρt(t) = ρt(t) - ρt(20oC) = ρt(t) - 0 = ρt(t), из-за чего величина температурного эффекта реактивности при любой средней температуре теплоносителя t обозначается не Δρt, а просто ρt.
Наконец, поскольку ТЭР есть изменение реактивности реактора, то и измеряется он в единицах реактивности (в а.е.р. (долях от единицы) или в процентах). Первые из указанных единиц чаще встречаются в научной и технической литературе (как более простые, интернациональные, понятные всем), а вторые - в операторской практике (они удобны в расчетах). В определении ТЭР зафиксировано, что аргументом для функции ρt(t) является средняя температура теплоносителя. С первого взгляда это кажется неверным, так как температурное поле в гетерогенной активной зоне энергетического ВВРочень неоднородно: в топливе твэлов температура выше, чем температура оболочек твэлов, а температура оболочек твэлов - выше температуры теплоносителя, а, главное, что во всех материалах активной зоны в силу действия теплотехнических законов даже в стационарном режиме реактора температуры распределены по разному и в различных пределах. А так как нам уже понятно, что каждый материал по-своему отзывается на одинаковые изменения температуры, это означает, чтокаждый материал активной зоны даже при одинаковых изменениях в них температуры вносит в общий температурный эффект реактивности свою лепту температурных изменений реактивности, отличающуюся по величине от вкладов в ТЭР реактора других материалов. При имеющемся в реальных реакторах неодинаковом разогреве топлива, замедлителя, теплоносителя и других конструкционных материалов активной зоны вклады каждого материала в общий температурный эффект реактивности тем более неоднозначны, и потому одно лишь изменение средней температуры теплоносителя не может быть ответственным за полное температурное изменение реактивности всего реактора. Понятно, что температурное изменение реактивности реактора должно определяться некоторой среднеэффективной величиной температуры активной зоны, в которой учитывались бы "весовые коэффициенты" температурных изменений реактивности каждого материала и неравномерность разогрева каждого материала активной зоны. Однако для определения такой температуры потребовалось бы решить задачу чрезвычайной сложности, более обширную, чем детальный теплотехнический и нейтронно-физический расчеты всего реактора.
Как же быть? В качестве определяющей температуры для оценки температурного эффекта реактивности вынужденно принимаетсясредняя температура теплоносителя, поскольку это температура, которую легко практически измерить. Серии термопар, поставленных на входе и выходе активной зоны, дают после усреднения результатов измерений точное представление о величинах температур теплоносителя на входе и выходе из активной зоны, а средняя арифметическая их величина tтср = 0.5(tтвх + tтвых) (10.1.1) - достаточно точное представление о средней температуре теплоносителя в активной зоне; хотя от входа к выходу теплоноситель увеличивает температуру нелинейно по длине ТВС, из-за небольшой разницы входной и выходной температур теплоносителя (не более 30 - 35оС) среднеарифметическое значение температуры теплоносителя почти не отличается от средневзвешенного её значения в активной зоне. К тому же практически измерение крайних температур теплоносителя и получение электрического сигнала, пропорционального величине средней температуры теплоносителя, не представляет собой сложной технической задачи по сравнению с измерением даже локальной температуры топлива (для чего понадобилось бы сверлить герметичную оболочку твэла для осуществления вывода электрического сигнала от микротермопары внутри твэла).
Более того, приняв в качестве аргумента для функции температурного эффекта реактивности реактора ρt(tт) среднюю температуру теплоносителя tт, мы по крайней мере получаем возможность экспериментально измерять величину составляющей общего температурного эффекта реактивности реактора, которая определяется только изменением температуры теплоносителя (для этого надо медленно, равномерно разогревать работающий на минимально-контролируемом уровне мощности (МКУМ) реактор от постороннего источника тепла с тем, чтобы температура топлива в его твэлах незначительно отличалась от температуры теплоносителя).
Если эксплуатировать ВВР от малых уровней мощности и до номинальной её величины при постоянном расходе теплоносителя через его активную зону, то появляется возможность экспериментально измерить величины температурного эффекта реактивности реактора путём его медленного или ступенчатого разогрева собственным теплом(путем медленного увеличения мощности реактора, обеспечивающего малую скорость разогрева - не более 10оС/час, - при которой нестационарный режим разогрева реактора можно с должной степенью точности считать квазистационарным). При этом измеренная экспериментально зависимость ρt(tт) будет однозначной (по крайней мере, на данный момент кампании), поскольку изменение среднеэффективной температуры топлива на разных уровнях мощности в процессе разогрева реактора будет в силу теплотехнических закономерностей взаимнооднозначно связано с изменением среднеэффективной температуры теплоносителя.


 .
.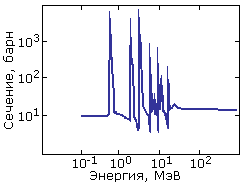 Рис.
2. Сечение радиационного захвата
нейтронов ядрами изотопа урана 238U
в резонансной области энергий
Рис.
2. Сечение радиационного захвата
нейтронов ядрами изотопа урана 238U
в резонансной области энергий Рис.
3. Схема цепной реакции в среде с
замедлителем
Рис.
3. Схема цепной реакции в среде с
замедлителем