Координати в просторі.

Прямокутна (декартова) система координат в просторі задається трійкою попарно перпендикулярних осей: OX — вісь абсцис, OY — вісь ординат, OZ — вісь аплікат.

В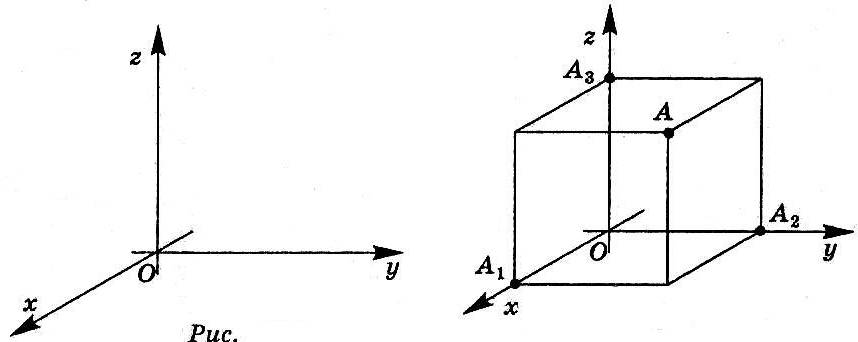 ідстань між точками та визначається формулою:

АВ=

Координати точки - середини відрізка АВ, де та , визначаються за формулами:

Координати кінця відрізка, якщо відомо координати початку і середини, визначаються так:

Координати точки поділу відрізка АВ, де та , у заданому відношенні n : m визначаються за формулами:

; ; .

Координати точки перетину медіан трикутника АВС, де , , визначаються за формулами:

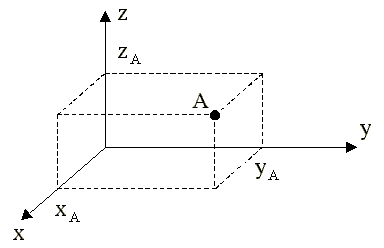К оординати проекцій точки A на осі координат, взяті за порядком нумерації осей, утворюють упорядковану систему трьох чисел. Цю трійку чисел називають прямокутними координатами точки A і позначають A (x; y; z).

Якщо точка належить осі OХ, то її координати (x; 0; 0), якщо осі OУ – (0; y; 0), якщо осі ОZ – (0; 0; z).

Якщо точка належить площині ХОУ, то її координата матиме вигляд (x; y; 0), якщо площині УОZ, то (0; y; z), якщо площині ХОZ, то (x; 0; z).

Тренувальні завдання.

1. Дано точки: E (0; 3; 0), F (0; 0; - 9), M (- 2; 0; 0), N (0; 1; - 3),

A (0; 0; 8), B (- 7; 3; 9), C (0; - 4; 0), D (6; 0; 0), K (0; 4; 7), L (1; 0; 9),

P (3; 7; 0), O (9; - 1; 9), R (0; 0; 5), S (4; - 6; 0), W (2; 0; 8), Т (0; 2; - 3). Вкажіть точки, які лежать:

• А) на координатній вісі ОХ:

• Б) на координатній вісі ОУ:

• В) на координатній вісі ОZ:

• Г) у координатній площині ХОУ:

• Д) у координатній площині УОZ:

• Е) у координатній площині ХОZ:

• Ж) у просторі:

Відповідь: А) М, D. Б) Е, С. В) F, А, R. Г) Р, S. Д) N, К, Т. Е) L, W. Ж) В, О.

2. Знайдіть координати середини відрізка FK, якщо:

F(8; - 2; 0), K(0; 8; - 6);

Зразок розв’язання:

Скористаємося формулами:

Обчислимо:

Відповідь: С (4; 3; - 3).

3. Точка М – середина відрізка АВ. Знайдіть координати точки В, якщо: А(8; - 4; 6), М(1; 2; 3).

Зразок розв’язання:

Скористаємося формулами:

Обчислимо:

Відповідь: В(- 6; 8; 0).

4. Знайдіть відстань між точками А і В, якщо: А(1; -7; - 4), В(4; - 5; 2).

Зразок розв’язання:

Скористаємося формулами: АВ=

Обчислимо: АВ=

Відповідь: 7 одиниць довжини.

5. Відстань між точками М(4; у; 2) і N(1; - 3; - 4) дорівнює 7. Знайдіть у.

Зразок розв’язання:

Скористаємося формулами: АВ=

Обчислимо:

Відповідь: у₁ = - 5, у₂ = -1.

6. В трикутнику АВС А(5; - 2; 0), В(- 1; 4; 3), С(5; 6; 7). Знайти довжину середньої лінії МN трикутника АВС, де М і N – середини сторін АС і ВС відповідно.

Зразок розв’язання:

1) Обчислимо координати точки М – середини сторони АС.

А(5; - 2; 0), С(5; 6; 7).

Скористаємося формулами:

М(5; 2; 3,5).

2) Обчислимо координати точки N – середини сторони ВС.

В(- 1; 4; 3), С(5; 6; 7).

Скористаємося формулами:

N(2; 5; 5).

3) Обчислимо довжину лінії МN трикутника АВС, де М(5; 2; 3,5), N(2; 5; 5).

Скористаємося формулами: АВ =

Обчислимо:

MN =

Відповідь: MN = 4,5 одиниць довжини.

7. Знайдіть координати точки Р, яка ділить відрізок FК у відношенні 3 : 1, рахуючи від точки F, якщо F(- 1; 7; -9), K(3; - 5; 7);

Зразок розв’язання:

Скористаємося формулами: ; ; .

Обчислимо: ;

Відповідь: Р (0; 4; -0,5).