8. Статистическое определение вероятности события. Аксиоматическое определение вероятности события.

Вероятностью события в статистическом смысле называется число , относительно которого стабилизируется (устанавливается) относительная частота при неограниченном увеличении числа опытов.

Относительная частота появления события – это отношение числа появлений события в серии из опытов к числу испытаний:

.

Вероятностью называется функция множеств, заданная на –алгебре пространства элементарных исходов и удовлетворяющая следующим условиям:

1. ;

2. , т.е. вероятность достоверного события равна единице;

3. Вероятность события , заключающееся в том, что наступит одно из попарно несовместных событий ( ), составляет

.

Эти условия должны выполняться и для бесконечных последовательностей попарно несовместных событий, т.е. должны выполняться также и условия в определении –алгебры . Таким образом, из условия 3 следует:

.

Эти условия составляют аксиомы теории вероятностей.

9. Условная вероятность и ее свойства.

Вероятность события , вычисленная при условии, что произошло другое событие , называется условной вероятностью события и обозначается .

Свойства условных вероятностей:

1. ;

2. ;

3. ;

4. Если , то ;

5. ;

6. ;

7. ;

8. .

10. Теоремы сложения вероятностей несовместных и совместных событий.

Формула умножения вероятностей

Теорема: Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие имело место:

.

Теорема: Вероятность произведения конечного числа событий равна произведению их условных вероятностей относительно произведения предшествующих событий:

.

Формула сложения вероятностей

Теорема: Вероятность суммы конечного числа несовместных событий равна сумме вероятностей этих событий:

.

Теорема: Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

.

11. Зависимые и независимые события.

Событие А называется независимым от события В, если его вероятность не зависит от того, произошло В или нет, т.е. критерий независимости:

Р(А)=Р(А/В)=Р(А/ ).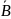

В противном случае, т.е. когда критерий не выполняется, событие А зависит от события В.

Зависимость и независимость всегда взаимны, т.е. если событие А не зависит от события В, то и событие В не зависит от события А:

Р(В)=Р(В/А)=Р(В/ ).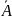

12. Формула полной вероятности события. Формулы Байеса.

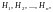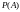Пусть событие A может наступить совместно только с одним из событий образующих полную группу несовместных событий (гипотез). Тогда вероятность появления события определяется по формуле полной вероятности:

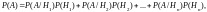
где – вероятность гипотезы

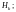
– условная вероятность события A при этой гипотезе.

Формула читается так: вероятность события A равна сумме произведений условных вероятностей этого события по каждой из гипотез на вероятности самих гипотез.

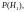
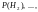
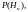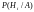Если вероятности гипотез до опыта были а в результате опыта появилось событие A, то условная вероятность с учетом появления события A вычисляется по формуле Байеса:

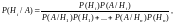
Если все гипотезы до опыта имеют одинаковую вероятность 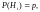формула Байеса принимает вид: