3. Достоверное и невозможное событие. Совместимые и несовместимые события. Противоположное событие.

Событие называется достоверным в данном опыте, если оно обязательно произойдет в этом опыте. Достоверное событие обозначают .

Событие называется невозможным, если в данном опыте оно не может произойти. Невозможное событие обозначают

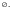
Несовместимые события – это события, которые вместе никогда не могут появиться.

Совместимые события – это события, которые могут появиться вместе.

Событием, противоположным событию A, называется событие 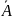которое наступает тогда и только тогда, когда не наступает событие А.

4. Операции над событиями (сумма, разность, произведение).

Суммой двух событий А и В (обозначается A +В или A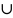 В) называется событие, состоящее из всех исходов, входящих либо в А, либо в В. Другими словами, под A+B понимают следующее событие: произошло или событие А, или событие В, либо они произошли одновременно, если это возможно.

Разностью двух событий А и В (обозначается A− В или A \ B) называется событие, состоящее из исходов, входящих в А, но не входящих в В.

Произведением двух событий А и В (обозначается АВ или A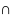 B) называется событие, состоящее из тех исходов, которые входят как в А, так и в В. Иными словами, АВ означает событие, при котором события А и В наступают одновременно.

5. Понятие о полной группе событий.

Множество попарно несовместных событий называют полной группой событий, если при любом исходе случайного эксперимента непременно наступает одно из событий, входящих в это множество. Другими словами, для полной группы событий выполнены следующие условия:

• появление одного из событий данного множества в результате испытания является достоверным событием, т.е. событие ;

• события и ( ) попарно несовместимы и – событие невозможное при любых , т.е. .

Простейшим примером полной группы событий является пара противоположных событий и .

Теорема. Сумма вероятностей событий полной группы равна единице:

.

6. Классическое определение вероятности события.

Вероятность события равна отношению числа равновозможных благоприятствующих элементарных исходов к общему числу всех равновозможных и единственно возможных элементарных исходов данного испытания:

,

где – число благоприятствующих событию исходов;

– общее число возможных исходов.

Из определения вероятности события следует, что , поэтому всегда выполняются неравенства , т.е. вероятность любого события есть неотрицательное число, не превышающее единицы.

Если , то событие невозможное.

Если , то событие достоверное.

7. Геометрическое определение вероятности события.

П усть на плоскости задана некоторая область D площадью S_D, в которой содержится другая d область площадью S_d (рис. 1). В область D наудачу бросается точка. Чему равна вероятность того, что точка попадет в область d? При этом предполагается, что наудачу брошенная точка может попасть в любую точку области D, и вероятность попасть в какую-либо часть области D пропорциональна площади части и не зависит от ее расположения и формы. В таком случае вероятность попадания в область d при бросании наудачу точки в область D.

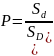
Таким образом, в общем случае, если возможность случайного появления точки внутри некоторой области на прямой, плоскости или в пространстве определяется не положением этой области и ее границами, а только ее размером, т. е. длиной, площадью или объемом, то вероятность попадания случайной точки внутрь некоторой области определяется как отношение размера этой области к размеру всей области, в которой может появляться данная точка. Это есть геометрическое определение вероятности.