42. Критерий согласия Пирсона о виде распределения.

Критерий согласия Пирсона (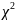 ). Алгоритм проверки:

1. Построить интервальный статистический ряд и гистограмму.

2. По виду гистограммы выдвинуть гипотезу:

• Н₀ – величина Х распределена по закону: F₀(x)=f₀(x),

• H₁ – величина Х не распределена по закону: F₀(x) 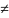f₀(x), где f₀(x), F₀(x) – плотность и функция гипотетического закона распределения.

3. Используя метод моментов или максимального правдоподобия, определить оценки неизвестных параметров 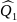, …, 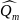гипотетического закона распределения.

4. Вычислить значение критерия по формуле:

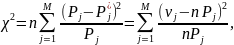(1)

где 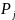– теоретическая вероятность попадания случайной величины в j –й интервал при уловии, что гипотеза Н₀ верна:

(2)

5. Из таблицы распеделения выбирается значение 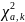, где a - заданный уровень значимости (a = 0,05 или а= 0,01), а k- число степеней свободы, которое определяется по формуле:

k=M-1-s,

где s – число неизвестных параметров гипотетического закона распределения.

6. Если значение, вычисленное по формуле (2), больше, чем критическое значение, т.е.

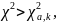
то гипотеза H₀ отконяется, в противном случае нет оснований ее отклонить.

43. Понятие о регрессионной зависимости случайных величин. Выборочные уравнения регрессии.

Под регрессией понимается функциональная зависимость между объясняющими переменными и условным математическим ожиданием (средним значением) зависимой переменной Y, которая строится с целью предсказания (прогнозирования) среднего значения Y при фиксированных значениях независимых переменных.

Так как реальные значения зависимой переменной не всегда совпадают с ее средним значением и могут быть различными при данном X (или ), зависимость должна быть дополнена некоторым слагаемым :

или

называются регрессионными моделями (или уравнениями).

По выборке ограниченного объема строится так называемое выборочное (эмпирическое) уравнение регрессии. В силу несовпадения статистической базы для генеральной совокупности и выборки оценки коэффициентов, входящих в уравнение регрессии, практически всегда отличаются от истинных значений, что приводит к несовпадению эмпирической и теоретической линий регрессии. Различные выборки из одной и той же генеральной совокупности обычно приводят к отличающимся друг от друга оценкам. Задача состоит в том, чтобы по конкретной выборке найти оценки неизвестных параметров так, чтобы построенная линия регрессии являлась бы наилучшей, среди всех других линий.

44. Линейная регрессия.

Если функция регрессии линейна, то говорят о линейной регрессии. Линейная регрессия является наиболее распространенным видом зависимости между экономическими переменными:

или

- теоретической линейной регрессионной моделью; коэффициенты – теоретическими параметрами регрессии; – случайным отклонением.

По выборке ограниченного объема строится выборочное уравнение регрессии:

, (1)

где – оценки неизвестных параметров , называемые выборочными коэффициентами регрессии, – оценка условного математического ожидания .

, (2)

где отклонение – оценка теоретического отклонения .

Коэффициенты должны быть такими, чтобы случайные отклонения были минимальны.

Если по выборке требуется определить оценки выборочного уравнения регрессии (2), то вводится в рассмотрение и минимизируется функция:

.

Выразив коэффициенты:

, (3)

где введены обозначения:

.