40. Проверка статистических гипотез. Нулевая и альтернативная гипотезы, статистический критерий. Ошибки первого и второго рода.

Проверка гипотезы о равенстве вероятностей: пусть произведено две серии опытов, состоящих соответственно из n₁ и n₂ опытов. В каждом из них регистрировалось появление одного и того же события А. В первой серии событие А появилось в k₁ опытах, во второй – в k₂ опытах, причем частота события А в первой серии получилась больше, чем во второй:

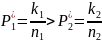
Разность между двумя частота получилась равной U = P₁^* – P₂^* (1). Выдвинем двухальтернативную гипотезу {H0, H1}(H0- нулевая гипотеза, а H1- альтернативная гипотеза), где:

• H0 – различия в вероятностях не существует, т.е. обе серии опытов произведены в одинаковых условиях, а расхождение U объясняется случайными причинами;

• H1 – различие в вероятностях существует, т.е. обе серии опытов произведены не в одинаковых условиях.

В данном случае гипотеза H0 состоит в том, что обе серии опытов однородны и что вероятность P появления события А в них одна и та же, приближенно равная частоте, которая получится, если обе серии смешать в одну:

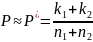
При достаточно больших n₁ и n₂ каждая из случайных величин P₁^* и P₂^*распределена практически нормально, с одним и тем же математическим ожиданием m= P ≈ P* . Что касается дисперсий D₁ и D₂ в первой и во второй сериях, то они различны и равны соответственно:

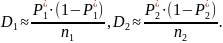
В качестве критерия будем использовать случайную величину U = P₁^* – P₂^*, которая также имеет приближенно нормальное распределение с математическим ожиданием m_U =0 и дисперсией:

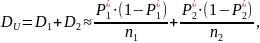
Откуда

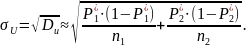
Определим критическую точку U_α для заданного уровня значимости α из уравнения:

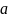=P(U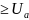 )=0,5-Ф( 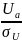), т.е. U_α =

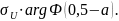
Если значение, вычисленное по формуле (1), больше, чем критическое значение, т.е. U_α > U , то гипотеза H0 отклоняется, в противном случае нет оснований ее отклонить.

Статическим критерием называется случайная величина U =Ф ( x₁, K , x_n ) ,где x_i –значения выборки, которая позволяет принять или отклонить нулевую гипотезу H0.

Ошибка первого рода состоит в том, что будет отклонена гипотеза H0, если она верна. Вероятность совершить ошибку первого рода обозначается α и называется уровнем значимости. Наиболее часто на практике принимают, что α = 0,05 или α = 0,01.

Ошибка второго рода заключается в том, что гипотеза H0 принимается, если она неверна. Вероятность ошибки этого рода обозначается β. Вероятность не допустить ошибку второго рода (1-β) называют мощностью критерия.

41. Этапы проверки статистической гипотезы.

Этапы проверки статистической гипотезы:

1. По выборочным данным формулируют нулевую Н0 и альтернативную Н1 гипотезы.

2. Задают уровень значимости α (0,05 или 0,01).

3. В зависимости от Н0 определяют статистический критерий K = f(x₁, …, x_n), имеющий известное распределение.

4. По выборке и формуле критерия K рассчитывают наблюдаемое значение критерияK_набл для этого в формулу критерия K = f(x₁, …, x_n) вместо (x₁, …, x_n) подставляют конкретные числа, полученные в результате наблюдений, и подсчитывают числовое значение критерия.

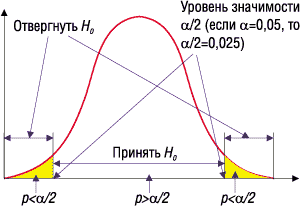
5. В зависимости от вида конкурирующей гипотезы и распределения критерия выбирают вид расположения критической области: правосторонняя, левосторонняя или двусторонняя. Границы (критические точки) при заданном уровне значимости находят из соотношений для критических областей:

• правосторонней: P(K>K_кр) = α;

• левосторонней: P(K<K_кр) = α;

• двусторонней: P(K<K_кр) = α /2 и P(K>K_кр) = α /2.

6. По результатам проверки: K_набл 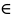W ?- делают вывод о принятии или отклонении гипотезы Н0. Если K_набл попадает в критическую область W, то гипотеза Н₀ отвергается и принимается гипотеза Н₁ (на рис. 2 двусторонняя критическая область W показана желтым цветом). Если K_набл не попадает в критическую область, гипотеза Н₀ не отвергается (принимается).