Анализ переходных процессов в электрических цепях

Одноконтурная электрическая цепь (рис.3.1) разбита на три участка. Первый содержит последовательно включенные R, L или R, C элементы, второй R, L, C и третий – R либо L элемент с параллельно подключенным ключом К₂. Параметры цепи приведены в табл. 3.1. Исходное положение К₂ обозначено: разомкнутое – нулем, замкнутое – единицей.

Рис.3.1

Т Р Е Б У Е Т С Я:

Студенты заочного отделения выполняют только пункты 1 и 2.

1. Начертить схему для своего варианта задания и привести все заданные параметры.

2. Рассчитать классическим методом переходный ток при следующих двух коммутациях:

а) при t = 0 ключом К₁ цепь подключают на постоянное напряжение U, указанное в табл. 3.1 (начальные условия – нулевые);

б) в момент t₁ замыкается ключ К₂, если он был разомкнут, или размыкается, если был замкнут.

3. Рассчитать символическим методом установившийся гармонический ток в цепи, полученной в п.2,б, при синусоидальном напряжении, действующее значение которого U дано в табл. 3.1. Частота f и начальная фаза синусоидального напряжения приведены в табл. 3.2. Построить временную диаграмму тока i(t).

4. Рассчитать операторным методом переходный ток в цепи (считать момент коммутации t = 0) при замыкании ключа К₂, если он был предварительно разомкнут, или при размыкании К₂, если он был замкнут.

Определить начальные условия. Построить составляющие переходного тока и результирующий ток. На отдельном графике (для сравнения) начертить результирующий переходный ток и установившийся гармонический ток (п.3)

Таблица 3.1

Вар.	Участок 1			Участок 2			Участок 3
№	R1 Ом	L1 мГн	C1 мкФ	R2 Ом	L2 мГн	C2 мкФ	R3 Ом	L3 мГн	K2	U В	t1 мс
1	13	13		40,45	7	40		70	1	25	2
2	2,3		37	2,8	24	52	15		0	65	4
3	25	10		25	15	43		173	1	22	4
4	60	15		80	27	32		38	0	35	5
5	4,7		50	5,2	70	70	80		1	54	8
6	11	12		14	23	48	40		0	27	10
7	160		6	140	60	8		55	1	45	1
8	120	38		150	73	83	200		1	80	25
9	5,5		110	7,5	48	171	70		1	29	20
10	150		23	140	23	25		61	0	37	2,5
11	2,4		60	2,7	65	79	36		0	75	18
12	2,8	27		3	40	77	160		1	31	17,5
13	2,1	11		3,2	9	28		10	1	20	8
14	55		43	90	43	39	100		1	49	4
15	7,3		150	7,7	78	213	135		1	33	21
16	29	17		28	12	77		24	0	23	5
17	4,8		160	5,2	88	253	140		1	35	23
18	115		53	130	50	75	150		0	90	15
19	4,5		13	5,3	18	17		22	1	17	2,2
20	66	18		37	80	23	47		0	70	2
21	72		27	91	35	29		27	0	43	3
22	3,8	8		5,2	10	6	58		1	77	1,5
23	2,7	14		26	16	35		25	1	30	6
24	180	45		160	78	90	300		0	63	50
25	15	19		11	20	37		17	0	21	6
26	48	21		64	28	28	85		1	57	2,5
27	4,5		19	5,3	22	21		27	1	15	3
28	2,2	40		2,5	76	85	25		0	61	15
29	7,1		31	5,1	33	35		29	0	40	5
30	91		45	81	47	33	60		1	51	3

Таблица 3.2

Вар. №	f, Гц	u, град	Вар. №	f, Гц	u, град
1	120	50	16	440	95
2	180	75	17	110	-55
3	240	10	18	640	185
4	300	110	19	680	200
5	360	130	20	160	215
6	150	15	21	620	20
7	560	170	22	200	190
8	600	195	23	520	180
9	540	-25	24	100	30
10	580	0	25	400	140
11	74	220	26	340	120
12	85	-35	27	280	100
13	320	125	28	80	85
14	140	105	29	300	30
15	95	-45	30	160	70

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

1. Схема электрической цепи для варианта № … приведена на рис.3.2 (К₂, например, в положении 1)

Вариант № … U = 45 В R1 = 5,8 Ом R2 = 10,2 Ом R3 = 144 Ом L2 = 0,098 Гн C1 = 20010-6 Ф C2 = 23510-6 Ф t1 = 0,015 с

Рис.3.2

2.а Расчет классическим методом переходного тока при замыкании ключа К₁ (ключ К₂ остается замкнутым). Электрическая схема цепи после первой коммутации показана на рис.3.3 (начальные условия нулевые).

Рис.3.3

2 .1. Составляется исходное дифференциальное уравнение при обходе контура

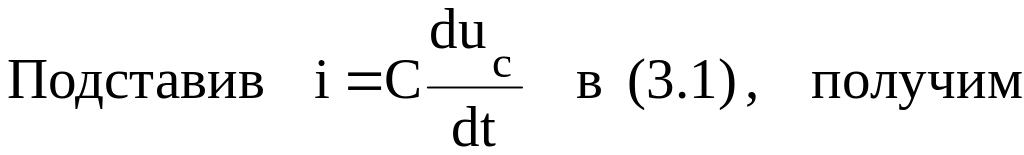
2.2. Решение уравнения (3.2) ищем в виде суммы принужденной и свободной составляющих:

где u_{с пр} = U.

2.3. Для определения свободной составляющей u_{с св} составим однородное дифференциальное уравнение из (3.2)

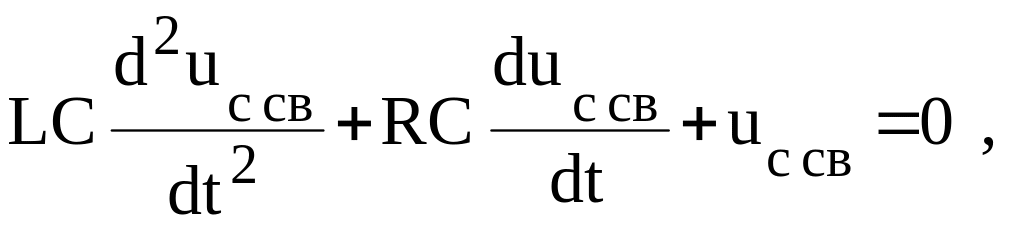
или, разделив на LC,

Тогда характеристическое уравнение

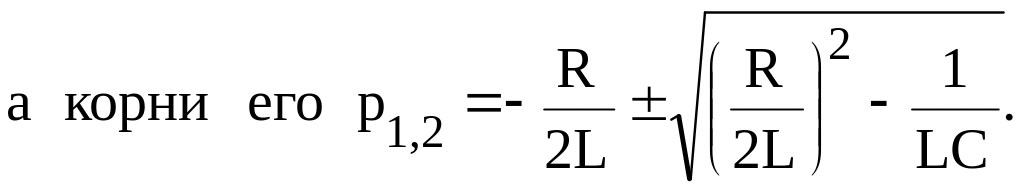
Если р₁ и р₂ вещественные и разные, то свободная составляющая находится в форме

где А₁, А₂ – постоянные интегрирования.

Если р₁ = р₂ = р, то

и постоянными интегрирования являются А и .

4. Возвращаясь к п. 2.2 (с учетом (3.4)), найдем постоянные интегрирования А₁, А₂ из двух уравнений

При нулевых начальных условиях система (3.7) примет вид

Д ля колебательного режима (корни р₁, р₂ – комплексные) система (3.7) изменится:

С учетом начальных условий (при t = 0):

И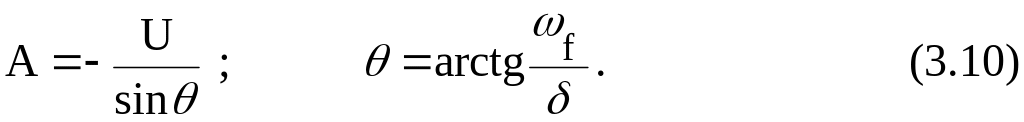 з (3.9) определим:

После нахождения постоянных интегрирования напряжение на емкости (3.7) для апериодического режима:

и переходный ток

Для колебательного режима из (3.8) получим:

где А и  определены в (3.10).

Расчетные данные свести в табл. 3.3.

Таблица 3.3

Первая коммутация
Момент коммутации	Начальные условия	р1	р2
t = 0	uc(0) = 0 i(0) = 0

Построить u_c(t), i(t) по уравнениям (3.11)  (3.14).

2.б Схема электрической цепи после второй коммутации (размыкание К₂) приведена на рис.3.4.

Рис.3.4

Начальные условия для второй коммутации u_c(t₁) и i(t₁) рассчитать по уравнениям (3.11)  (3.14), подставив t= t₁ (см. табл. 3.1)

С оставляем исходное дифференциальное уравнение (подобное (3.1), (3.2), но где R = R₁ +R₂ +R₃), ищем решение его аналогично п.п. 2.1  2.4. Отличие от уравнений (3.7), (3.8) в том, что начальные условия ненулевые, поэтому система (3.7) примет вид:

Р ешение (3.15) относительно неизвестных А₁, А₂ приведет к следующим выражениям (студент может проверить их самостоятельно):

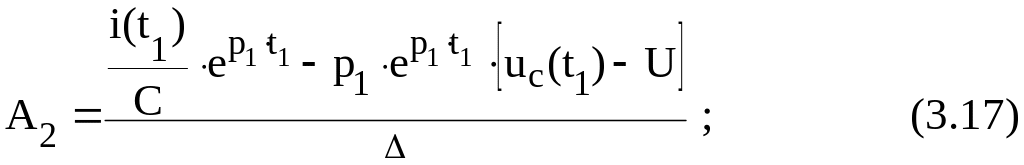
Д ля колебательного режима система (3.8) становится:

Если для упрощения записи обозначить через произвольные коэффициенты В и 

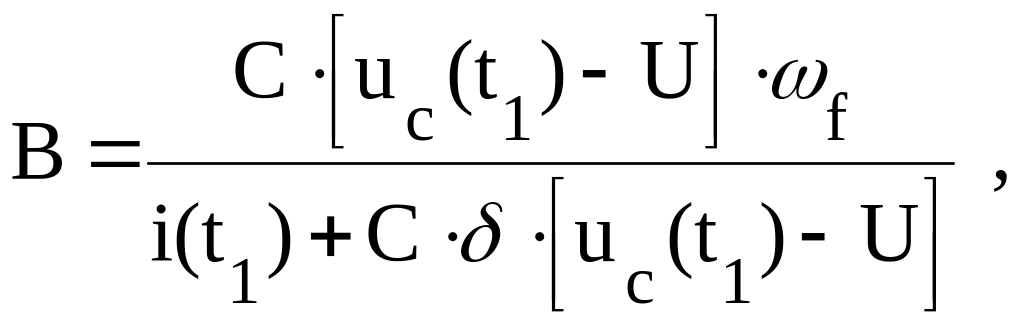
то решение системы (3.18), относительно неизвестных А и , приведет к следующим соотношениям:

 =  _f t₁ ; (3.19)

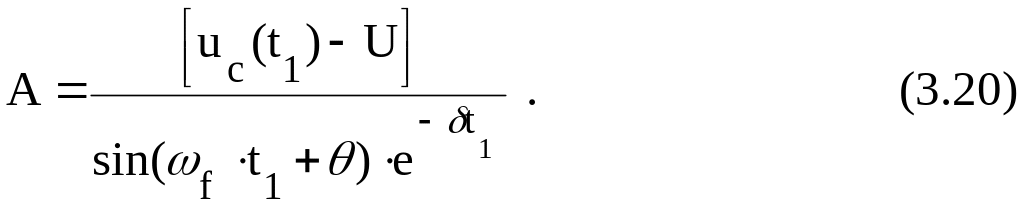
Таким образом, u_c(t) и i(t) описываются системой (3.7) для апериодического режима, где А₁ и А₂ определяются из (3.16) и (3.17).

В случае колебательного режима u_c(t) и i(t) описываются системой (3.8), в которой  и А рассчитываются с помощью (3.19), (3.20).

Расчетные данные свести в табл. 3.4.

Таблица 3.4

Вторая коммутация
Момент коммутации	Начальные условия	р1	р2
t1=	uc(t1) = i(t1) =

Построить кривую переходного тока по вторым уравнениям системы (3.7) или (3.8). На отдельном графике эту кривую совместить с переходным током из п. 2.4.

3. Схема в символической форме (согласно пункту 2.б) при установившемся гармоническом напряжении показана на рис.3.5.

Вариант №… U = 45 В f = 125 Гц u = 75 град R1 = 5,8 Ом R2 = 10,2 Ом R3 =144 Ом L2 =0,098 Гн C1 = 20010-6 Ф C2 = 23510-6 Ф

Рис.3.5

3 .1. Комплексное сопротивление цепи

где R = R₁ +R₂ +R₃, L = L₂, С = С₁С₂ / (C₁+C₂).

3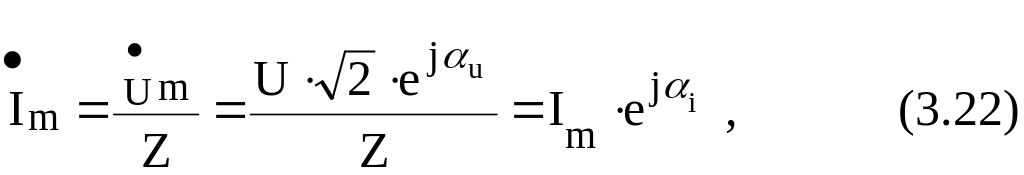 .2. Комплексная амплитуда тока

и амплитуда комплексного напряжения на емкости С

3.3. Переход от комплекса к i(t). Домножим (3.22) на оператор е ^jt – получим комплекс мгновенного значения тока :

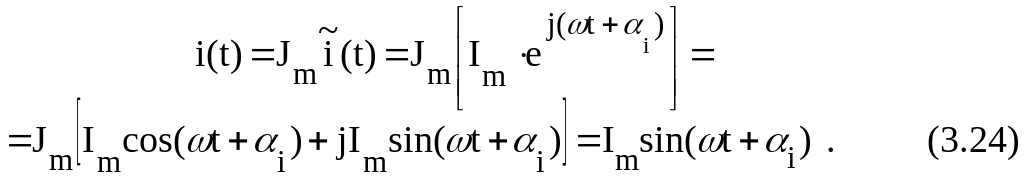
Аналогично получим напряжение на емкости

3.4. Подставим t = 0 в (3.24), (3.25):

Построить временную диаграмму синусоидального тока в установившемся режиме по уравнению (3.24).

4. Схема электрической цепи в операторной форме после коммутации ключа К₂ (замыкание) при ненулевых начальных условиях приведена на рис.3.6,а или (с учетом того, что

R = R₁ + R₂, L = L₂, C = C₁C₂ / C₁+C₂ ) на рис.3.6,б.

Рис.3.6

В этих схемах – изображение комплекса мгновенного значения , где = e ^jt , – изображение комплекса мгновенного значения тока, Z(p) = R + pL +1/pC – операторное сопротивление цепи для послекоммутационного режима.

4 .1. Ненулевые начальные условия в индуктивности в операторной форме

Ненулевые начальные условия в емкости в операторной форме

2. Операторное выражение для переходного тока нетрудно определить из схемы (рис.3.6):

После преобразования (3.30) ток можно представить в виде отношения полинома числителя N(p) к полиному знаменателя М(р):

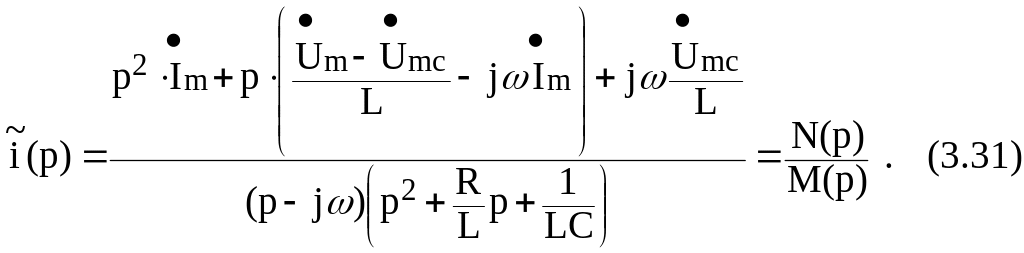
4.3. По теореме разложения определяется комплекс мгновенного значения тока (в функции времени):

где p_k – корни уравнения М(р) = 0; N(p_k) – значения полинома N(p) при p = p_k; М^’(p_k) – значения производной от полинома

позволяет определить принужденную и свободные составляющие при условии n  m (n – степень полинома числителя, m – степень полинома знаменателя). Однако она не применима в т акой форме, если при M(p) = 0 имеются кратные корни.

Выражения N(p) и M^’(p_k), полученные из (3.31):

Тогда (3.32) примет вид

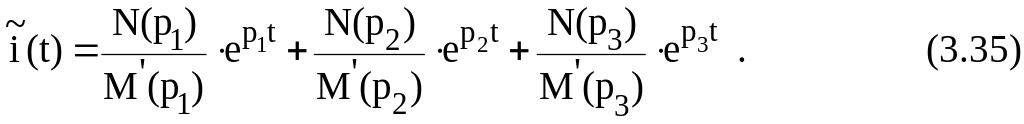
Обозначим:

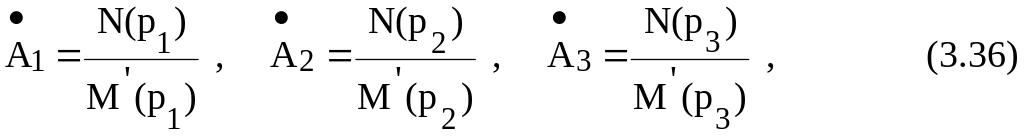
Основные расчетные данные свести в табл. 3.5.

Таблица 3.5

Начальные условия			Начальные условия (в опер. ф.)		Корни знаменателя
i(0)	uc(0)				p1	p2	p3

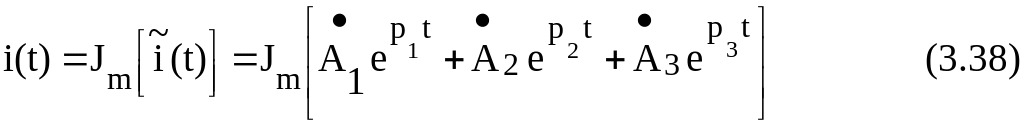4. П о комплексу мгновенного значения тока ((3.32), (3.37)) определяется переходной ток как мнимая часть данного комплекса:

Таким образом, переходной ток состоит из трех составляющих:

 принужденная составляющая,

а два других тока:

 свободные составляющие.

Построить i₁(t), i₂(t), i₃(t) и результирующий ток i(t). На отдельном графике построить результирующую кривую (уравнение (3.39)) и гармонический ток в установившемся режиме (уравнение (3.24)) для сравнительного анализа.