
Расчет электрической цепи переменного тока
Даны электрические схемы с шестью ветвями и тремя взаимноиндуктивными связями (для нечетных вариантов предназначена схема на рис.2.1,а; для четных – схема на рис.2.1,б). Коэффициенты связи между соответствующими ветвями приведены в табл.2.1. каждая ветвь содержит последовательно соединенные активное сопротивление, индуктивность, емкость и источник ЭДС (все источники – одной и той же частоты).
В табл.2.3 указаны действующие значения ЭДС и начальные фазы источников (в градусах), причем положительным направлениям ЭДС соответствуют направления стрелок на рис.2.1, для ЭДС, отмеченных звездочками, направления считать противоположными. Значения ЭДС даны в вольтах, сопротивлений – в омах.
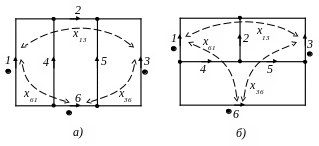
Рис.2.1
Одноименные полюсы катушек индуктивностей считать в начале каждой катушки. Если при движении вдоль ветви (по стрелке) конец катушки встречается раньше, чем начало (такая индуктивность помечена звездочкой в табл.2.3), то следует изменить расположение одноименных полюсов катушек индуктивностей на рис.2.1.
Номер контура, для которого необходимо построить векторную диаграмму, указан в табл.2.2.
Таблица 2.1
№ вар. |
k13 |
k36 |
k61 |
№ вар. |
k13 |
k36 |
k61 |
1 |
0,81 |
0,56 |
0,2 |
16 |
0,35 |
0,25 |
0,15 |
2 |
0,87 |
0,42 |
0,12 |
17 |
0,15 |
0,32 |
0,91 |
3 |
0,8 |
0,08 |
0,11 |
18 |
0,75 |
0,25 |
0,14 |
4 |
0,47 |
0,33 |
0,88 |
19 |
0,89 |
0,57 |
0,17 |
5 |
0,19 |
0,43 |
0,64 |
20 |
0,41 |
0,2 |
0,13 |
6 |
0,97 |
0,42 |
0,46 |
21 |
0,19 |
0,3 |
0,87 |
7 |
0,84 |
0,45 |
0,38 |
22 |
0,29 |
0,18 |
0,41 |
8 |
0,19 |
0,99 |
0,66 |
23 |
0,85 |
0,59 |
0,21 |
9 |
0,98 |
0,31 |
0,17 |
24 |
0,22 |
0,79 |
0,29 |
10 |
0,09 |
0,55 |
0,54 |
25 |
0,23 |
0,83 |
0,61 |
11 |
0,05 |
0,97 |
0,51 |
26 |
0,63 |
0,25 |
0,81 |
12 |
0,95 |
0,53 |
0,07 |
27 |
0,45 |
0,41 |
0,96 |
13 |
0,1 |
0,35 |
0,93 |
28 |
0,86 |
0,46 |
0,4 |
14 |
0,18 |
0,88 |
0,33 |
29 |
0,63 |
0,16 |
0,96 |
15 |
0,9 |
0,55 |
0,13 |
30 |
0,94 |
0,3 |
0,19 |
Таблица 2.2
№ вар. |
№ контура |
№ вар. |
№ контура |
№ вар. |
№ контура |
1 |
3 |
11 |
1 |
21 |
3 |
2 |
1 |
12 |
3 |
22 |
2 |
3 |
2 |
13 |
1 |
23 |
3 |
4 |
1 |
14 |
2 |
24 |
1 |
5 |
2 |
15 |
3 |
25 |
3 |
6 |
3 |
16 |
3 |
26 |
1 |
7 |
2 |
17 |
2 |
27 |
1 |
8 |
3 |
18 |
1 |
28 |
2 |
9 |
1 |
19 |
2 |
29 |
3 |
10 |
2 |
20 |
1 |
30 |
2 |
Таблица 2.3 |
3 |
xC |
24 |
33 |
29 |
35 |
51 |
37 |
12 |
39 |
70 |
41 |
xL |
92 |
38 |
40 |
36 |
60٭ |
34٭ |
32 |
32 |
48٭ |
30٭ |
||
r |
81 |
71 |
53 |
73 |
48 |
75 |
25 |
77 |
57 |
79 |
||
αe |
30 |
12 |
90 |
–16 |
55 |
20 |
–25 |
–24 |
85 |
32 |
||
E |
24 |
85 |
81 |
90 |
13 |
95 |
95٭ |
99٭ |
80 |
20 |
||
2 |
xC |
77 |
92 |
13 |
94 |
65 |
96 |
98 |
99 |
27 |
11 |
|
xL |
41 |
80 |
55 |
82 |
12 |
84 |
64 |
86 |
46 |
88 |
||
r |
25 |
41 |
42 |
43 |
86 |
45 |
94 |
47 |
14 |
49 |
||
αe |
20 |
–20 |
80 |
15 |
–45 |
–10 |
15 |
0 |
75 |
–13 |
||
E |
99 |
50 |
39 |
48 |
32٭ |
46٭ |
57 |
44 |
20 |
42 |
||
1 |
xC |
52 |
62 |
26 |
64 |
43 |
66 |
69 |
68 |
80 |
70 |
|
xL |
53 |
50 |
36٭ |
52٭ |
45 |
54 |
88 |
56 |
47٭ |
58٭ |
||
r |
97 |
11 |
39 |
13 |
32 |
15 |
57 |
17 |
18 |
19 |
||
αe |
10 |
95 |
–70 |
–90 |
35 |
85 |
–10 |
–80 |
65 |
75 |
||
E |
20 |
10 |
86٭ |
15٭ |
60 |
20 |
13 |
25 |
18 |
30 |
||
|
№ ветви |
№ вар. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
продолжение таблицы 2.3 |
6 |
xC |
16 |
47 |
53 |
49 |
81 |
51 |
80 |
55 |
19 |
57 |
xL |
56 |
32 |
73 |
34 |
9 |
36 |
62٭ |
38٭ |
66 |
46 |
||
r |
84 |
43 |
58 |
39 |
34 |
37 |
73 |
35 |
95 |
33 |
||
αe |
60 |
–27 |
25 |
–27 |
58 |
31 |
–12 |
10 |
35 |
–43 |
||
E |
84 |
41 |
88 |
43 |
69 |
45 |
76 |
47 |
68 |
49 |
||
5 |
xC |
31 |
93 |
20 |
95 |
88 |
97 |
14 |
98 |
57 |
13 |
|
xL |
32 |
18 |
55 |
16 |
98 |
14 |
70 |
12 |
23 |
10 |
||
r |
78 |
67 |
88 |
65 |
51 |
63 |
63 |
61 |
50 |
60 |
||
αe |
50 |
45 |
15 |
45 |
45 |
–22 |
0 |
55 |
25 |
-65 |
||
E |
63 |
71 |
26 |
73 |
34 |
75 |
32 |
77 |
11 |
79 |
||
4 |
xC |
73 |
63 |
17 |
65 |
18 |
67 |
47 |
69 |
25 |
71 |
|
xL |
28 |
48 |
54 |
46 |
20 |
44 |
23 |
42 |
52 |
40 |
||
r |
74 |
97 |
56 |
95 |
53 |
93 |
26 |
91 |
78 |
89 |
||
αe |
40 |
–10 |
0 |
–10 |
15 |
0 |
20 |
–30 |
–15 |
0 |
||
E |
41 |
11 |
56 |
13 |
33 |
15 |
39 |
17 |
93٭ |
19٭ |
||
|
№ ветви |
№ вар. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
продолжение таблицы 2.3 |
3 |
xC |
29 |
43 |
30 |
45 |
99 |
47 |
80 |
49 |
81 |
51 |
xL |
83٭ |
28٭ |
13 |
26 |
44٭ |
24٭ |
63 |
22٭ |
90٭ |
20٭ |
||
r |
58 |
81 |
13 |
83 |
63 |
85 |
10 |
87 |
28 |
89 |
||
αe |
15 |
–36 |
75 |
42 |
–33 |
–46 |
82 |
48 |
–24 |
–52 |
||
E |
43 |
18 |
78 |
16 |
82 |
14 |
28٭ |
12٭ |
89 |
10 |
||
2 |
xC |
53 |
13 |
56 |
15 |
64 |
17 |
34 |
19 |
51 |
21 |
|
xL |
66 |
90 |
54 |
92 |
69 |
94 |
91 |
96 |
85 |
98 |
||
r |
98 |
51 |
51 |
53 |
76 |
55 |
86 |
57 |
61 |
59 |
||
αe |
5 |
17 |
–65 |
–21 |
–22 |
23 |
72 |
–27 |
0 |
31 |
||
E |
12 |
40 |
9 |
38 |
60٭ |
36٭ |
52 |
34 |
57 |
32 |
||
1 |
xC |
75 |
72 |
87 |
74 |
30 |
76 |
15 |
78 |
49 |
80 |
|
xL |
97 |
60 |
19٭ |
62٭ |
56٭ |
64٭ |
33٭ |
66٭ |
42 |
68 |
||
r |
12 |
21 |
9 |
23 |
60 |
25 |
52 |
27 |
57 |
29 |
||
αe |
0 |
–70 |
–55 |
65 |
12 |
–60 |
0 |
55 |
–17 |
–50 |
||
E |
48 |
35 |
34 |
40 |
30٭ |
45٭ |
76 |
50 |
51 |
55 |
||
|
№ ветви |
№ вар. |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
продолжение таблицы 2.3 |
6 |
xC |
84 |
59 |
98 |
61 |
42 |
63 |
43 |
67 |
99 |
69 |
xL |
42٭ |
42٭ |
22٭ |
44٭ |
45٭ |
46٭ |
97 |
48 |
22 |
50٭ |
||
r |
19 |
31 |
51 |
29 |
45 |
27 |
21 |
25 |
79 |
23 |
||
αe |
–45 |
47 |
–50 |
–49 |
63 |
0 |
–90 |
–51 |
64 |
53 |
||
E |
96 |
51 |
50٭ |
53٭ |
89 |
55 |
13 |
57 |
88٭ |
59٭ |
||
5 |
xC |
17 |
17 |
77 |
21 |
54 |
25 |
59 |
29 |
24 |
31 |
|
xL |
30 |
12 |
24 |
14 |
53 |
16 |
95 |
18 |
24 |
20 |
||
r |
37 |
59 |
57 |
57 |
36 |
58 |
14 |
53 |
18 |
51 |
||
αe |
0 |
75 |
90 |
0 |
52 |
85 |
0 |
–90 |
44 |
0 |
||
E |
24٭ |
81٭ |
30 |
83 |
23 |
85 |
52 |
87 |
35٭ |
89٭ |
||
4 |
xC |
59 |
73 |
62 |
75 |
73 |
77 |
69 |
79 |
53 |
81 |
|
xL |
36 |
38 |
60 |
36 |
42 |
34 |
93 |
32 |
69 |
30 |
||
r |
84 |
87 |
22 |
85 |
15 |
83 |
71 |
81 |
17 |
79 |
||
αe |
25 |
–40 |
85 |
50 |
0 |
62 |
–42 |
0 |
–34 |
–70 |
||
E |
46 |
21 |
68 |
23 |
14 |
25 |
16٭ |
27٭ |
86 |
29 |
||
|
№ ветви |
№ вар. |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
продолжение таблицы 2.3 |
3 |
xC |
35 |
53 |
37 |
55 |
39 |
57 |
41 |
59 |
43 |
63 |
xL |
15 |
18 |
25٭ |
16 |
35٭ |
14 |
45 |
12٭ |
55٭ |
18٭ |
||
r |
65 |
91 |
67 |
93 |
69 |
95 |
71 |
97 |
81 |
98 |
||
αe |
0 |
64 |
–65 |
–66 |
–80 |
68 |
0 |
–72 |
–66 |
74 |
||
E |
35٭ |
13٭ |
37٭ |
17٭ |
39 |
19٭ |
41٭ |
21٭ |
45 |
25 |
||
2 |
xC |
23 |
23 |
25 |
25 |
29 |
27 |
31 |
29 |
33 |
31 |
|
xL |
10 |
48 |
20 |
46 |
30 |
44 |
40 |
42 |
50 |
40 |
||
r |
96 |
61 |
94 |
63 |
92 |
65 |
90 |
67 |
88 |
69 |
||
αe |
–84 |
–39 |
–48 |
43 |
–21 |
-47 |
24 |
49 |
0 |
–51 |
||
E |
21٭ |
30٭ |
33 |
28٭ |
43 |
26٭ |
53 |
24٭ |
62٭ |
22٭ |
||
1 |
xC |
79 |
87 |
15 |
84 |
17 |
86 |
19 |
88 |
21 |
90 |
|
xL |
16 |
70٭ |
17٭ |
72 |
19 |
74٭ |
11٭ |
76 |
13٭ |
78٭ |
||
r |
87 |
31 |
85 |
33 |
83 |
36 |
81 |
37 |
79 |
39 |
||
αe |
74 |
45 |
0 |
–40 |
–19 |
35 |
-48 |
–30 |
–33 |
25 |
||
E |
25 |
60 |
35 |
65٭ |
45 |
70٭ |
35٭ |
75٭ |
65 |
80 |
||
|
№ ветви |
№ вар. |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
продолжение таблицы 2.3 |
6 |
xC |
37 |
71 |
39 |
73 |
41 |
75 |
45 |
77 |
49 |
79 |
xL |
24٭ |
52٭ |
27 |
54 |
28٭ |
56 |
30٭ |
58 |
34٭ |
62٭ |
||
r |
32 |
21 |
35 |
19 |
38 |
17 |
41 |
15 |
44 |
13 |
||
αe |
12 |
–57 |
90 |
61 |
60 |
10 |
90 |
–64 |
-40 |
67 |
||
E |
62 |
61 |
64 |
63 |
66 |
65 |
70 |
67٭ |
72٭ |
69٭ |
||
5 |
xC |
19 |
36 |
21 |
40 |
23 |
44 |
27 |
43 |
31 |
41 |
|
xL |
12 |
22 |
14 |
24 |
16 |
26 |
18 |
28 |
20 |
30 |
||
r |
57 |
50 |
55 |
49 |
53 |
47 |
51 |
45 |
49 |
43 |
||
αe |
–47 |
–13 |
–27 |
17 |
–68 |
–21 |
50 |
23 |
–37 |
0 |
||
E |
16 |
91 |
18 |
93 |
20٭ |
95٭ |
22٭ |
97٭ |
38 |
98 |
||
4 |
xC |
45 |
83 |
49 |
85 |
51 |
87 |
13 |
89 |
16 |
94 |
|
xL |
13 |
28 |
26 |
26 |
54 |
84 |
52 |
22 |
32 |
20 |
||
r |
68 |
77 |
66 |
75 |
64 |
73 |
62 |
71 |
60 |
60 |
||
αe |
40 |
80 |
–24 |
–90 |
0 |
0 |
46 |
–15 |
30 |
35 |
||
E |
15 |
31 |
17٭ |
33٭ |
19٭ |
35٭ |
24 |
37٭ |
27٭ |
39٭ |
||
|
№ ветви |
№ вар. |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
Требуется:
1. Рассчитать
взаимно индуктивные сопротивления
(![]() ,
,
![]() ,
,
![]() ).
).
2. Начертить схему для своего варианта задания. Под ней привести все заданные и вычисленные параметры.
Перечертить схему заново, но в символической форме и привести все параметры в символической форме.
3. Методом контурных токов (МКТ) рассчитать токи во всех ветвях. Результаты свести в табл.2.4, 2.5.
4. Составить систему уравнений по законам Кирхгофа, подставить туда параметры цепи, найденные значения токов и проверить правильность расчета по МКТ.
Для каждой ветви выписать значения ЭДС как в символической, так и во временной формах и свести их в табл.2.6.
5. Построить векторную диаграмму в выбранном масштабе на комплексной плоскости для контура, указанного в табл.2.2 (номер контура в схеме считать слева направо).
6. Рассчитать энергетический баланс всей электрической цепи.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
1. Взаимные
индуктивные сопротивления
определяются из коэффициентов связи
(![]() ),
заданных в табл.2.1, следующим образом:
),
заданных в табл.2.1, следующим образом:
![]()
где
![]() – номера соответствующих ветвей.
– номера соответствующих ветвей.
2. Один из вариантов схемы приведен на рис.2.2.
Схема в символической форме примет вид, показанный на рис.2.3.
Вариант №…
![]() В;
В;
![]()
![]() Ом;
Ом;
![]() Ом;
Ом;
![]() Ом;
Ом;
![]() В;
В;
![]()
![]() Ом;
Ом;
![]() Ом;
Ом;
![]() Ом;
Ом;
![]()
…
![]()

![]()
![]()
![]()
Р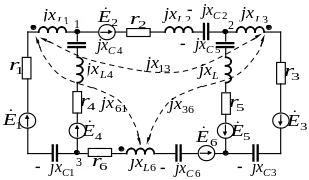 ис.2.2
ис.2.2
Рис.2.3
Вариант №…
![]() В;
В;
![]() Ом;
Ом;
![]() Ом;
Ом;
![]() Ом;
Ом;
![]() В;
Ом;
В;
Ом;
![]() Ом;
Ом;
![]() Ом;
Ом;
![]()
…
![]()
![]()
![]()
![]()
3. Расчет методом контурных токов цепи переменного тока производится так же, как и цепи постоянного тока, только вместо ЭДС, токов и сопротивлений в основной системе уравнений берутся соответствующие комплексы.
3.1. Определяем количество уравнений, которое необходимо и достаточно согласно МКТ, оно равно числу независимых контуров .
3.2. Выбираем направления контурных токов (рис.2.2) и составляем систему:
![]() (2.1)
(2.1)
где
![]() ,
,
![]() ,
,
![]() –
комплексы собственных сопротивлений
контуров;
–
комплексы собственных сопротивлений
контуров;
![]() ,
,
![]() ,
,
![]() – комплексы взаимных сопротивлений
контуров;
,
– комплексы взаимных сопротивлений
контуров;
,
![]() ,
– комплексы контурных ЭДС.
,
– комплексы контурных ЭДС.
3.3. Комплексы взаимных сопротивлений контуров:
![]()
![]() (2.2)
(2.2)
![]()
Слагаемые в
квадратных скобках определяются по
правилам, указанным в задании 1, а
взаимно индуктивные составляющие –
в зависимости от ориентации контурных
токов относительно одноименных
полюсов катушек (если контурные токи
одинаково ориентированы относительно
одноименных полюсов катушек, то
![]() берется с знаком плюс, и, наоборот,
при разной ориентации контурных токов
это сопротивление учитывается с
знаком минус).
берется с знаком плюс, и, наоборот,
при разной ориентации контурных токов
это сопротивление учитывается с
знаком минус).
3.4. Комплексы собственных сопротивлений контуров:
![]() ;
;
![]()
![]() ; (2.3)
; (2.3)
![]() .
.
Взаимно индуктивные сопротивления учитываются в собственных сопротивлениях только тогда, когда есть индуктивные связи внутри данного контура (остальные правила – те же).
3.5. Комплексы контурных ЭДС:
 (2.4)
(2.4)
3.6. Система (2.1)
решается относительно контурных токов
![]() ,
,
![]() ,
,
![]() .
Для вычисления токов в ветвях
предварительно зададимся их
направлениями, например, как показано
на рис.2.1, тогда
.
Для вычисления токов в ветвях
предварительно зададимся их
направлениями, например, как показано
на рис.2.1, тогда
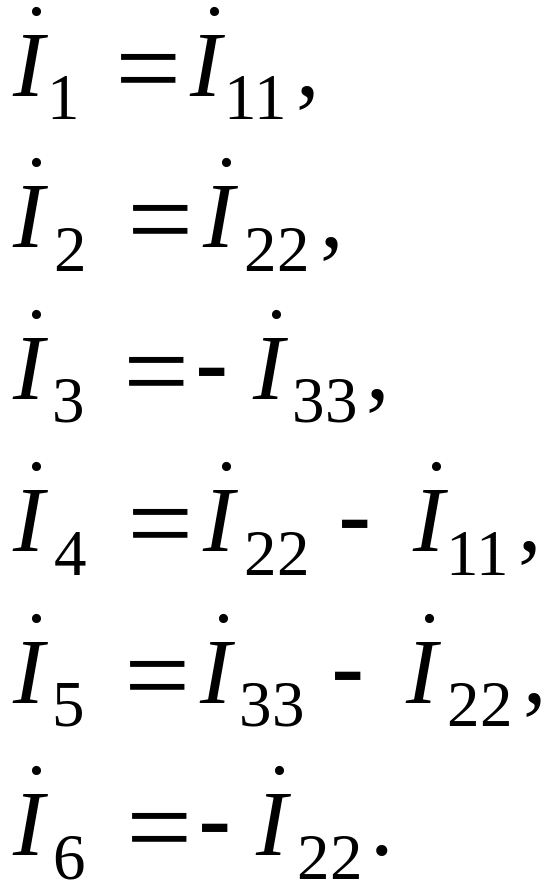 (2.5)
(2.5)
Таблица 2.4
Ток |
A |
A |
A |
A |
A |
A |
A |
A |
A |
Модуль |
|
|
|
|
|
|
|
|
|
Аргумент (град) |
|
|
|
|
|
|
|
|
|
3.7. Привести
аналитические выражения для мгновенных
значений токов ветвей (![]() )
и свести их в табл.2.5.
)
и свести их в табл.2.5.
Таблица 2.5
Ветвь |
|
|
, A |
, A |
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
4. Прежде, чем
составлять систему уравнений по
законам Кирхгофа, определяется общее
количество необходимых уравнений.
Оно равно числу ветвей в схеме –
.
Количество уравнений по первому
закону Кирхгофа – (![]() ),
где
– число узлов. Число уравнений по
второму закону Кирхгофа равно
.
),
где
– число узлов. Число уравнений по
второму закону Кирхгофа равно
.
4.1. Система уравнений в символической форме по первому закону Кирхгофа имеет вид:
![]() (2.6)
(2.6)
Раскроем подробнее выражение (2.6) для узлов 1, 2, 3 соответственно (рис.2.3, а направление токов в ветвях см. рис.2.1):
![]() (2.7)
(2.7)
![]()
4.2. Система уравнений в символической форме по второму закону Кирхгофа:
![]() (2.8)
(2.8)
составляется так
же, как и в цепях постоянного тока, но
появляются слагаемые, связанные с
взаимной индуктивностью, которые
учитываются по следующему правилу. Если
направление обхода элемента m
и ток в ветви с элементом n
одинаково
ориентированы по отношению к одноименным
полюсам индуктивности, то
![]() берется с положительным знаком, и,
наоборот, если направление обхода
элемента m
и ток в ветви с элементом n
по разному ориентированы по отношению
к одноименным полюсам индуктивности,
то
имеет знак минус. Поэтому выражения
(2.8) для первого, второго и третьего
контуров (рис.2.3) соответственно примут
вид (направления обхода контуров – по
часовой стрелке):
берется с положительным знаком, и,
наоборот, если направление обхода
элемента m
и ток в ветви с элементом n
по разному ориентированы по отношению
к одноименным полюсам индуктивности,
то
имеет знак минус. Поэтому выражения
(2.8) для первого, второго и третьего
контуров (рис.2.3) соответственно примут
вид (направления обхода контуров – по
часовой стрелке):
![]()
![]() ,
(2.9)
,
(2.9)
![]()
![]() (2.10)
(2.10)
![]()
![]() (2.11)
(2.11)
Погрешность выполнения равенств (2.9) (2.11) находится отдельно для вещественных и мнимых частей, в каждом случае она не должна превышать пяти процентов.
Выписать и свести в таблицу значения ЭДС в каждой ветви.
Таблица 2.6
Ветвь |
|
, B |
|
, B |
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
5. Прежде, чем строить векторную диаграмму по, например, первому контуру, необходимо составить уравнение по второму закону Кирхгофа (уравнение (2.9)) и вычислить все составляющие этого уравнения.
На комплексной
плоскости выбирается масштаб для
векторов напряжения и строится
векторная диаграмма на миллиметровой
бумаге. При правильном построении
векторы, просуммированные по правилу
многоугольника, например, в левой
части выражения (2.9), совпадут с
геометрической суммой векторов (![]() )
в правой части.
)
в правой части.
6. Энергетический баланс мощностей, развиваемых источниками ЭДС и потребляемых в цепи, проверяется следующим образом.
6.1. Для активных мощностей:
![]() (2.12)
(2.12)
где в левой части
– алгебраические суммы активных
мощностей источников,
![]() .
Если мощность окажется отрицательной
(
.
Если мощность окажется отрицательной
(![]() ),
то это означает, что данный источник
потребляет активную мощность (например,
вместо генератора
электродвигатель). В правой части
(2.12) – арифметическая сумма мощностей,
рассеиваемых на активных сопротивлениях.
Подробная запись (2.12) для схемы
(рис.2.3) имеет вид:
),
то это означает, что данный источник
потребляет активную мощность (например,
вместо генератора
электродвигатель). В правой части
(2.12) – арифметическая сумма мощностей,
рассеиваемых на активных сопротивлениях.
Подробная запись (2.12) для схемы
(рис.2.3) имеет вид:
![]()
![]() (2.13)
(2.13)
Если направление источника ЭДС и тока ветви не совпадает, то слагаемые в левой части берутся с знаком минус.
6.2. Для реактивных мощностей:
![]() (2.14)
(2.14)
где в левой части
– алгебраическая сумма реактивных
мощностей источников. Если мощность
отрицательная (![]() ),
значит источник потребляет реактивную
мощность. В правой части (2.14) первое
слагаемое – реактивные индуктивные
мощности, второе слагаемое – реактивные
емкостные мощности, третье слагаемое
– реактивные мощности, обусловленные
взаимно индуктивными связями между
катушками (
),
значит источник потребляет реактивную
мощность. В правой части (2.14) первое
слагаемое – реактивные индуктивные
мощности, второе слагаемое – реактивные
емкостные мощности, третье слагаемое
– реактивные мощности, обусловленные
взаимно индуктивными связями между
катушками (![]() – действующие значения токов в ветвях
взаимно связанных катушек,
– действующие значения токов в ветвях
взаимно связанных катушек,
![]() – угол сдвига между начальными фазами
токов в ветвях,
– угол сдвига между начальными фазами
токов в ветвях,
![]() )
. Знак плюс берется при согласном
включении катушек, а минус – при
встречном включении. Подробная запись
выражения (2.14):
)
. Знак плюс берется при согласном
включении катушек, а минус – при
встречном включении. Подробная запись
выражения (2.14):
![]()
![]()
![]() (2.15)
(2.15)
![]()
![]()
где
![]()
![]()
![]() Значения
Значения
![]() ,
,
![]() ,
,
![]() нетрудно
определить из табл.2.4.
нетрудно
определить из табл.2.4.
Согласное или встречное включение катушек в правой части выражения (2.14) определяется ориентацией токов в ветвях по отношению к одноименным полюсам катушек (если токи в индуктивно связанных ветвях одинаково ориентированы по отношению к одноименным полюсам, то включение – согласное, и, наоборот, если токи в ветвях по разному ориентированы по отношению к одноименным полюсам катушек, то включение – встречное).
П Р И М Е Р
1. Пусть задано:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
тогда
,
тогда
![]() ,
,
![]() ,
,
![]() .
.
2. Один из вариантов схемы приведен на рис.2.2, где
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Схема в символической форме показана на рис.2.3, где
![]()
![]()
![]()
![]() (В);
(В);
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3. Расчет цепи методом контурных токов.
3.1. Определяем
количество уравнений:
![]() = 6 – (4 – 1) = 3, где
= 6 – (4 – 1) = 3, где
![]() ,
,
![]() .
.
3.2. Выбираем направление контурных токов (по часовой стрелке, рис.2.2, 2.3) и составляем систему уравнений:
(2.1)
3.3. Рассчитаем комплексы взаимных сопротивлений между контурами согласно (2.2):
![]()
![]() ;
;
![]()
![]() ;
;
![]() .
.
3.4. Определяем по (2.3) комплексы собственных сопротивлений контуров:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3.5. Комплексы контурных ЭДС согласно (2.4) равны:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3.6. Решение системы (2.1) дает:
![]()
![]()
![]()
Токи в ветвях с учетом (2.5):
![]()
![]()
![]()
![]()
![]()
![]()
Значения контурных токов и токов в ветвях сведены в табл.2.4.
Таблица 2.4
Ток |
A |
A |
A |
A |
A |
A |
A |
A |
A |
Модуль (А) |
0,546 |
0,267 |
0,421 |
0,546 |
0,267 |
0,421 |
0,722 |
0,65 |
0,267 |
Аргумент (град) |
109,91 |
11,415 |
208,239 |
109,91 |
11,415 |
28,239 |
51,645 |
166,993 |
168,586 |
3.7. Аналитические
выражения для мгновенных значений
токов в ветвях нетрудно получить из
табл.2.4. Например, для первой ветви
![]() ,
поэтому
,
поэтому
![]()
![]() ,
где
,
где
![]() ,
а мгновенное значение тока
,
а мгновенное значение тока
![]() .
Остальные токи приведены в табл.2.5.
.
Остальные токи приведены в табл.2.5.
Таблица 2.5
Ветвь |
, А |
, A |
, A |
, A |
1 |
|
|
0,772 |
0,546 |
2 |
|
|
0,378 |
0,267 |
3 |
|
|
0,595 |
0,421 |
4 |
|
|
1,021 |
0,722 |
5 |
|
|
0,919 |
0,65 |
6 |
|
|
0,378 |
0,267 |
4. Общее количество
уравнений по законам Кирхгофа:
.
Число уравнений по первому закону
Кирхгофа:
![]() .
Количество уравнений по второму закону
Кирхгофа:
.
Количество уравнений по второму закону
Кирхгофа:
![]() .
.
4.1. Проверим справедливость системы (2.7):

![]()
4.2. Оценим тождественность уравнения (2.9):
![]()
![]()
![]()
![]()
С другой стороны:
![]()
Уравнение (2.10):
![]()
![]()
![]()
![]()
![]()
![]()
С другой стороны:
![]()
![]()
Уравнение (2.11):
![]()
![]()
![]()
![]() .
.
С другой стороны:
![]() .
.
В каждом уравнении погрешность в пределах нормы.
Мгновенные значения ЭДС для всех ветвей сведены в табл.2.6.
Таблица 2.6
Ветвь |
, В |
|
|
, В |
1 |
|
|
35,36 |
25 |
2 |
|
|
130,108 |
92 |
3 |
|
|
18,385 |
13 |
4 |
|
|
66,468 |
47 |
5 |
|
|
96,167 |
68 |
6 |
|
|
100,409 |
71 |
5. Вычислим все составляющие в левой части уравнения (2.9):
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
6)
![]()
7)
![]()
8)
![]()
Составляющие в правой части уравнения (2.9):
9)
10)
![]()
Чтобы не перегружать
диаграмму (рис.2.4), сложим отдельно
первые три вектора в п. 5 и обозначим
![]() :
:
![]()
Сумму четвертого,
пятого и шестого векторов в п. 5
обозначим
![]() :
:
![]()
Сложим
седьмой и восьмой векторы п. 5, обозначив
через
![]() :
:
![]()
Просуммируем
![]() на комплексной плоскости и убедимся,
что их геометрическая сумма равна
на комплексной плоскости и убедимся,
что их геометрическая сумма равна
![]() (см. рис.2.4).
(см. рис.2.4).
 Рис.2.4
Рис.2.4
6. Энергетический баланс мощностей.
6.1. Для активных мощностей согласно (2.13):
![]()
![]()

С другой стороны:
![]()
6.2. Для реактивных мощностей из (2.15) следует:
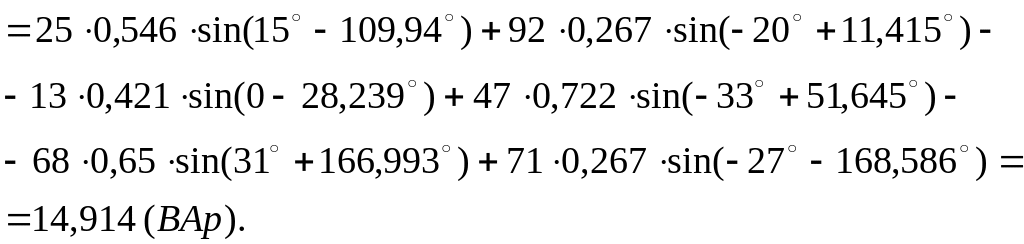
Правая часть уравнения (2.15) дает:

![]()
![]()
![]()

З А ДА Н И Е № 3
