Содержание

Введение………………………………………………………………………4

1 Теоретическая часть……………………………………………………….5

1.1 Ряды предпочтительных чисел………………………………………...5

1.2 Идентификация, классификация и кодирование изделий и конструкторско-технологических документов…..……………………………….10

1.3 Нормоконтроль…………………………………………..……………..14

2 Практическая часть………………………………………………………..19

2.1 Система предпочтительных чисел в стандартизации………………..19

2.2 Классификация и кодирование изделий и конструкторских документов………………..………………………………………………………...20

2.3 Провести анализ стандартов ГОСТ Р 54318-2011 и ГОСТ 4.464-86..…………………………………………………………………….21

2.4 Нормоконтроль конструкторского документа………………………..24

2.5 Определение целесообразности изготовления ступиц зубчатых колес по ряду Ra20, Ra10, Ra5………………………………………………………..…25

Приложение А – Чертеж детали «Вал»…………………….…………….30

Приложение Б – Сборочный чертеж «Функциональная ячейка»….…..31

Библиография…………………………………………………………….….32

Введение

В процессе трудовой деятельности специалисту приходится решать систематически повторяющиеся задачи: измерение и учет количества продукции, составление технической и управленческой документации, измерение параметров технологических операций, контроль готовой про­дукции, упаковывание поставляемой продукции и т.д. С решением этих задач помогает стандартизация.

Стандартизация – деятельность по установлению правил и характеристик в целях их добровольного многократного использования, направленная на достижение упорядоченности в сферах производства и обращения продукции и повышение конкурентоспособности продукции, работ или услуг.

Цель стандартизации – выявле­ние наиболее правильного и экономичного варианта, т.е. нахождение оптимального решения. Найденное решение дает возможность достичь оптимального упорядочения в определенной области стандартизации. Для превращения этой возможности в действительность необходимо, чтобы найденное решение стало достоянием большого числа предприя­тий (организаций) и специалистов. Только при всеобщем и многократном использовании этого решения существующих и потенциальных задач возможен экономический эффект от проведенного упорядочения.

Целью данной курсовой работы является знакомство с основами стандартизации, необходимыми специалисту. В курсовой работе рассматривается система предпочтительных чисел, классификация и кодирование изделий и конструкторской документации, анализ нормативных документов, а также нормоконтроль.

1 Теоретические сведения

1. Ряды предпочтительных чисел

1.1.1 Система предпочтительных чисел (ПЧ) позволяет наилучшим образом осуществлять согласование параметров и размеров отдельно взятого изделия со всеми связанными с ним видами продукции. Например: комплект изделий с присоединительными и посадочными местами.

В приборостроении и машиностроении ПЧ приняты в основу назначений линейных и угловых размеров, классов точности, размеров радиусов, гантелей, каналов, параметров шероховатости и т. д. Благодаря этому значительно возрастает уровень взаимозаменяемости, сокращается номенклатура режущего измерительного инструмента, калибров, штампов, пресс-форм, достигается более экономичный раскрой материалов.

На базе ПЧ строятся так называемые параметрические стандарты, в которых по единой закономерности стандартизуемых величин выбираются не только геометрические характеристики, а другие более сложные: мощность, частота вращения, давление, напряжение электрического тока, грузоподъемность и т.д. Это предотвращает производство неоправданно большой номенклатуры изделий.

Смысл системы ПЧ заключается в выборе лишь тех значений размеров, параметров, характеристик, которые подчиняются строго определенной математической закономерности, а не любых значений, получаемых в результате расчетов, проектирования или принимаемых в порядке волевого решения. Предпочтительными эти числа называются потому, что они рекомендуются для предпочтительного применения при конструировании, расчетах, стандартизации и унификации.

1.1.2 Чаще всего ряды ПЧ строятся на основе геометрической прогрессии, реже на основе арифметической прогрессии. Кроме того, есть разновидности рядов построенных на основе «золотого» сечения, двоичные ряды, комплементарные ряды и. т.д.

Ряды, построенные по арифметической прогрессии, характеризуются тем, что разность (интервал) значений двух соседних членов остается неизменной во всем диапазоне ряда, т.е.

,

где – значения рядом стоящих членов ряда; – разность (интервал) значений между двумя смежными членами ряда.

Графическое изображение рядов, построенных по арифметической, ступенчато-арифметической и геометрической прогрессиям показано на рисунке 1.

Рисунок 1 - Ряды, построенные по арифметической (а), ступенчато-арифметической (в) и геометрической (б) прогрессиям

На рисунке 1 этот ряд показан прямой «а». Арифметический ряд прост, не требует округления чисел, но его существенным недостатком является относительная неравномерность. При постоянной абсолютной разности относительная разность с увеличением номера члена ряда резко уменьшается.

Недостаток заключается в то, что наблюдается нецелесообразная разреженность значений в зоне малых величин и сгущенность их в зоне больших величин. Поэтому чаще применяются ступенчато-арифметические ряды, показанные на рисунке 2 прямой «в». Любой член ряда в пределах данной группы может быть вычислен по формуле:

,

где – первый член ряда; – разность прогрессии; – номер искомого числа.

1.1.3 Длительная практика стандартизации показала, что наиболее удобными являются ряды, построенные на основе геометрической прогрессии, так как при этом получается одинаковая относительная разность между любыми членами ряда. В геометрической прогрессии, имеющей в числе членов единицу, каждый член ряда определяется из выражения:

,

где - знаменатель прогрессии, - порядковый номер члена прогрессии, начиная с нуля.

Геометрическая прогрессия обладает следующими свойствами:

1. Отношение двух смежных членов всегда постоянно и равно знаменателю прогрессии:

;

2. Произведение или частное от деления любых членов прогрессии всегда является ее членом:

;

Целая положительная или отрицательная степень любого члена прогрессии всегда является членом этой прогрессии

;

3. Произвольный член , прогрессии определяется из выражения

,

где - член прогрессии, принятый за начальный.

1.1.4 Ряды R5, R10, R20, R 40 впервые введены Ренаром для диаметров канатов.

Рекомендациями Международной электротехнической комиссии (МЭК) установлены ряды с обозначением Е, применяемые в радиоэлектронике ЕЗ, Е6, Е24, Е48, Е96, Е192.

Предпочтительные числа рядов приведены в таблицах 1 и 2.

На базе рядов Е в частности построены параметрические стандарты на номинальное значение сопротивления резисторов и емкостей конденсаторов. По этим ГОСТам установлены следующие максимально допустимые отклонения в номиналах: Е3, Е6 ±20%; Е12 ±10%; Е24 ±5%.

Знаменатели рядов предпочтительных чисел приведены в таблице 3.

Таблица 1 – Предпочтительные числа рядов R5, R10, R20, R40

№ числа	Предп. числа	№ числа	Предп. числа	№ числа	Предп. числа	№ числа	Предп. числа	№ числа	Преп. числа
1	1,06	9	1,70	17	2,65	25	4,25	33	6,70
2	1,12	10	1,80	18	2,80	26	4,50	34	7,10
3	1,18	11	1,90	19	3,00	27	4,75	35	7,50
4	1,25	12	2,00	20	3,15	28	5,00	36	8,00
5	1,32	13	2,12	21	3,35	29	5,30	37	8,50
6	1,40	14	2,24	22	3,55	30	5,60	38	9,00
7	1,50	15	2,36	23	3,75	31	6,00	39	9,50
8	1,60	16	2,50	24	4,00	32	6,30	40	10,00

Таблица 2 - Предпочтительные числа рядов Е3, Е6, Е12, Е24

1,1	1,6	2,4	3,6	5,1	7,5
1,2	1,8	2,7	3,9	5,6	8,2
1,3	2,0	3,0	4,3	6,2	9,1
1,5	2,2	3,3	4,7	6,8	10,0

Таблица 3 - Знаменатели рядов предпочтительных чисел

Условные обозначения	Знаменатель ряда, q			Количество членов в десятичном интервале
	Точное значение	Округленное значение
R5		1,60	5
R10		1,25	10
R20		1,12	20
R40		1,06	40
R80		1,03	80
R160		1,015	160
E3		2,20	3
E6		1,50	6
E12		1,20	12
E24		1,10	24
E48		1,05	48
E96		1,025	96
E192		1,012	192

1.1.5 Ряды ПЧ обладают свойствами геометрической прогрессии.

Ряды ПЧ не ограничиваются в обоих направлениях, при этом числа менее 1,0 и более 10 получают делением или умножением на 10, 100 и т.д. За исходный ряд принимают члены прогрессии, расположенные в интервале от 1,0 до 10. При этом число 1,0 обязательно имеющееся в ряду, не входит в десятичный интервал 1,0<a≤10. Его следует рассматривать как завершающее число предыдущего десятичного интервала 0,1<а≤1,0.

Порядковые номера чисел представляют собой логарифмы чисел ряда при основании 10.

где – номер предпочтительного числа; 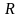– число значений ПЧ в десятичном интервале (номер ряда).

По указанной формуле можно найти номер ПЧ, также это можно осуществить, используя формулу

,

где – номер числа в нулевом интервале (1,0 <а ≤ 10 ); – целое положительное или отрицательное число, определяющее удаление рассматриваемого интервала в ту или другую сторону от нулевого; – число значений ПЧ в десятичном интервале (номер ряда).

Нахождение номера ряда можно осуществлять, используя определения определение знаменателя ряда:

R=1/lgq,

где q – знаменатель ряда.

В практике вычислений для упрощения расчетов по взаимосвязанным показателям стандартов используется известное свойство логарифмов, позволяющее вместо умножения или деления самих предпочтительных чисел соответственно складывать или вычитать номера этих чисел и по результирующему номеру определять искомое число. При этом удается, кроме ускорения вычислений, не оперировать округленными значениями чисел.

Возведение ПЧ в целую положительную или отрицательную степень производят путем умножения номера ПЧ на показатель степени и по полученному номеру находят соответствующее число в таблице.

1.1.6 Ограниченные ряды. При необходимости ограничения основных и дополнительных рядов в их обозначениях указываются предельные члены, которые всегда включаются в ограниченные ряды.

1.1.7 Выборочные ряды: это ряды, которые получают отбором каждого 1,2, 3, 4,...,i-го члена основного или дополнительного ряда, начиная с любого члена. В обозначение выборочного ряда обязательно присутствует косая черта, после которой указывается, какой член ряда подлежит выборке. Если ряд не ограничен, то должен быть указан хотя бы один член.

Выборочные ряды используются в тех случаях, когда уменьшение градаций создает дополнительный технический или экономический эффект по сравнению с использованием полных рядов. Пример: выборочный ряд R10/2 удачно применен для стандартизации круглых металлических стержней, что дает значительный экономический эффект.

1.1.8 Составные ряды. Ряды, получаемые путем сочетания различных основных и (или) выборочных рядов. Составной ряд в различных интервалах имеет неодинаковые знаменатели, однако конечные и начальные члены смежных рядов должны быть обязательно одинаковыми.

Составные ряды должны применяться, если требуемая плотность значений параметра в рассматриваемом интервале неодинакова.