
- •Рекомендуемая литература Основная литература:
- •Физические основы классической механики
- •Тема 1. Кинематика материальной точКи
- •1.1. Кинематика поступательного движения материальной точки
- •1.2. Кинематика вращательного движения материальной точки
- •1.3. Относительность движения
- •1.4. Основные уравнения прямолинейного движения и движения по окружности
- •Тема 2. Законы динамики. Закон сохранения импульса
- •2.1. Динамика материальной точки и поступательного движения
- •3.1 Фундаментальные взаимодействия в природе. Упругие свойства тел.
- •3.2 Механика сплошных сред
- •Тема 4. Основное уравнение вращательного движения. Закон сохранения момента импульса
- •4.1 Динамика вращательного движения
- •4.2. Момент инерции тел правильной геометрической формы относительно неподвижной оси вращения
- •4.3 Момент силы, момент импульса. Основное уравнение динамики вращательного движения
- •Тема 5. Механическая работа. Мощность.
- •Тема 6. Законы сохранения при вращательном движении
- •6.1 Закон сохранения момента импульса. Работа при вращении тела. Кинетическая энергия вращательного движения.
- •Тема 7. Взаимодействие электрических зарядов. Напряженность и потенциал электрического поля
- •7.1.Электрический заряд. Закон Кулона
- •7.2. Напряженность и потенциал электростатического поля,
- •Тема 8. Применение теоремы гаусса к расчету электростатических полей
- •8.1 Поток вектора напряженности электростатического поля (пвэн). Теорема Гаусса
- •Тема 9. Диэктрики, проводники и конденсаторы
- •9.1. Диэлектрики. Электрическое поле в диэлектриках
- •9. 2. Электроемкость проводникoв и конденсаторов
- •8.3 Энергия системы точечных электрических зарядов, заряженных проводников и конденсаторов. Энергия электростатического поля. Объемная плотность энергии. Пондермоторные силы.
- •Тема 10. Постоянный электрический ток
- •10.1. Электрический ток, сила и плотность тока
- •10.2. Электродвижущая сила (эдс). Напряжение
- •10.3. Сопротивление проводников
- •10.4. Последовательное и параллельное соединение проводников
- •10.5. Закон Ома для однородного участка и замкнутой цепи.
- •10.6. Анализ обобщенного закона Ома
- •10.7. Правила Кирхгофа для разветвленных цепей
- •10.8. Работа и мощность тока
- •ТЕма 11. Магнитное поле
- •11.1. Основные характеристики магнитного поля
- •11.2. Закон Био -Савара – Лапласа и его применение
- •11.3. Закон Ампера. Взаимодействие параллельных токов.
- •11.4. Магнитное поле движущегося заряда
- •11.5. Действие магнитного поля на движущийся заряд. Сила Лоренца. Движение заряженных частиц в магнитном поле
- •11.6 Теорема о циркуляции вектора (закон полного тока для магнитного поля в вакууме) и ее применение к расчету магнитных полей
- •Тема 12. Работа в магнитном поле. Явление электромагнитной индукции. Энергия магнитного поля.
- •12.1. Поток вектора магнитной индукции (магнитный поток). Теорема Гаусса для поля
- •12.2 Работа по перемещению проводника и контура с током в магнитном поле
- •12.3. Закон Фарадея (закон электромагнитной индукции). Правило Ленца.
- •12.4. Индуктивность контура. Самоиндукция.
- •12.5 Токи при размыкании и замыкании цепи
- •12.6. Взаимная индукция. Трансформатор
- •12.7. Энергия магнитного поля.
- •12.8 Магнитные свойства вещества. Магнетики
- •12.9 Закон полного тока для магнитного поля в веществе. Циркуляция вектора
- •12.10 Условия на границе раздела двух магнетиков
- •12.11Основы теории Максвелла для электромагнитного поля
- •12.13 Уравнения Максвелла для электромагнитного поля
- •12.14 Следствия из уравнений Максвелла Свойства электромагнитных волн.
- •Тема 13. Механические колебания и волны
- •13.1 Механические колебания
- •13.2. Упругие волны
- •Тема 14. Электромагнитные колебания и волны.
- •14.1 Свободные электромагнитные колебания в идеализированном колебательном контуре
- •Тема 1 5. Законы идеальных газов
- •15.1 Макроскопические состояния
- •9.2 Уравнения состояния идеального газа. Изопроцессы
- •16.1 Идеальный газ как модельная термодинамическая система. Статистические распределения
- •17. Явление переноса в газах
- •17.1 Явления переноса в термодинамически неравновесных системах
- •Тема 18. Основы термодинамики
- •18.1 Внутренняя энергия и работа идеального газа. Первый закон термодинамики и его применение к изопроцессам
- •18.2 Теплоемкость идеального газа
- •18.3 Адиабатический процесс. Уравнение Пуассона
- •18.4 Тепловые двигатели. Цикл Карно и его кпд
- •18.4 Второй закон термодинамики. Неравенство Клаузиуса. Энтропия
Тема 6. Законы сохранения при вращательном движении
6.1 Закон сохранения момента импульса. Работа при вращении тела. Кинетическая энергия вращательного движения.
Закон сохранения момента импульса для замкнутой системы
|
Работа при вращении тела: ΔA = MzΔφ, где Δφ - угол поворота тела; Mz - момент силы относительно оси |
Кинетическая энергия тела, вращающегося вокруг неподвижной оси: , где J– момент инерции тела относительно оси, ω - его угловая скорость Кинетическая энергия тела, катящегося по плоскости без скольжения:
где m– масса тела; vc - скорость центра масс тела; J – момент инерции тела относительно оси, проходящей через центр масс; ω –угловая скорость тела |
Пример 8. На скамье Жуковского сидит человек и держит в вытянутых руках гири массой m =10 кг каждая. Расстояние от каждой гири до оси вращения скамьи l1 = 50 см. Скамья вращается с частотой n1 = 1,0 с-1. Как изменится частота вращения скамьи и какую работу A произведет человек, если он сожмет руки так, что расстояние от каждой гири до оси уменьшится до l2 = 20 см. Суммарный момент инерции человека и скамьи относительно оси вращения J =2,5 кг·м2. Ось вращения проходит через центр масс человека и скамьи.
Условие:
m = 10 кг;
l1=50 см = 0,5 м;
n1 =1,0 с-1;
l2 =20 см =0,2 м;
J = 2,5 кг·м2.
n2 - ? А - ?
Решение. Частота вращения скамьи Жуковского изменится в результате действий, производимых человеком при сближении гирь. В системе тел скамья – человек – гири все силы, кроме сил реакции опоры, являются внутренними и не изменяют момента импульса системы. Однако моменты сил реакции опоры относительно вертикальной оси равны нулю. (Для скамьи Жуковского силы трения в оси можно считать отсутствующими.) Следовательно, момент импульса этой системы остается постоянным:
![]() ;
;
![]() ,
(1)
,
(1)
где J1ω1, J2ω2 - моменты импульса системы соответственно до и после сближения гирь.
Перепишем векторное уравнение (1) в скалярном виде:
J1ω1 = J2ω2. (2)
До сближения гирь момент инерции всей системы: J1 = J0 + 2ml12.
После сближения: J2 = J0 + 2ml22,
где m - масса каждой гири.
Выражая угловую скорость через частоту вращения по формуле ω = 2πn и подставляя ее в уравнение (1) получаем
(J0 + 2ml12)n1 = (J0 + 2ml22)n2.
Откуда
 2,3 c-1.
2,3 c-1.
Все внешние силы не создают вращающего момента относительно оси и, следовательно, не совершают работы. Поэтому изменение кинетической энергии системы равно работе, совершенной человеком:
A
= W2
- W1
=![]() .
.
Учитывая, что ω2 = J1ω1/J2, получаем работу, совершаемую человеком:
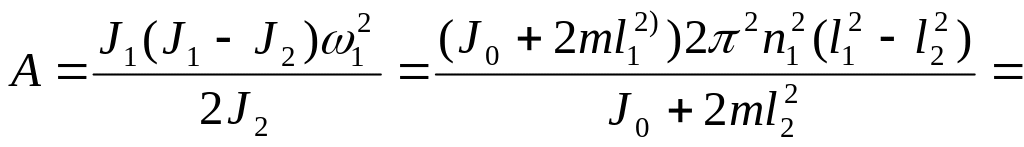 =
190 Дж.
=
190 Дж.
Тема 7. Взаимодействие электрических зарядов. Напряженность и потенциал электрического поля
7.1.Электрический заряд. Закон Кулона
Закон сохранения электрических зарядов В
замкнутой системе: Q
=
|
Дискретность электрических зарядов: Q = ne, где n= 1, 2... е = ± 1,6 . 10-19 Кл – элементарный электрический заряд |
Закон Кулона: в
векторной форме:
в
скалярной форме:
где F12 - сила взаимодействия двух точечных зарядов в вакууме; r - расстояние между зарядами; ε0 = 8,85·10-12 Ф·/м - электрическая постоянная |
Линейная
плотность зарядов: Поверхностная
плотность зарядов:
Объемная
плотность зарядов:
|
