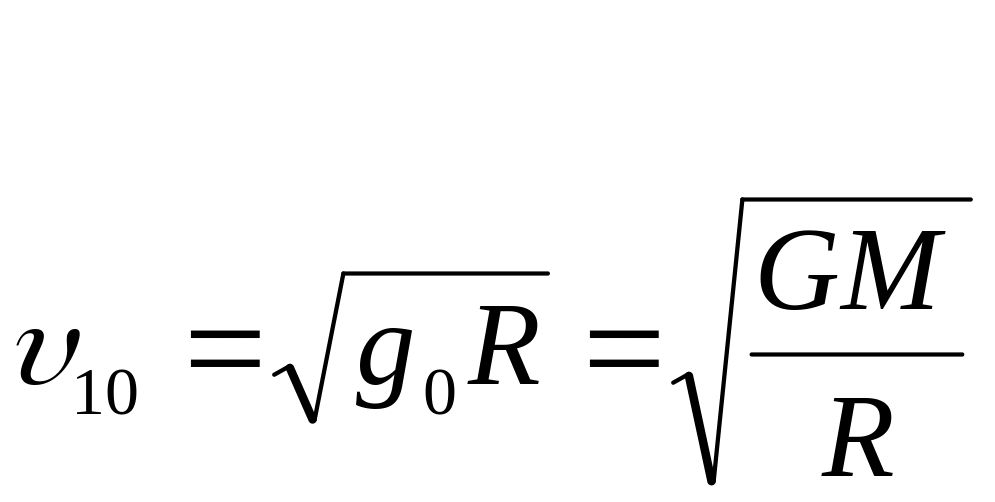- •Рекомендуемая литература Основная литература:
- •Физические основы классической механики
- •Тема 1. Кинематика материальной точКи
- •1.1. Кинематика поступательного движения материальной точки
- •1.2. Кинематика вращательного движения материальной точки
- •1.3. Относительность движения
- •1.4. Основные уравнения прямолинейного движения и движения по окружности
- •Тема 2. Законы динамики. Закон сохранения импульса
- •2.1. Динамика материальной точки и поступательного движения
- •3.1 Фундаментальные взаимодействия в природе. Упругие свойства тел.
- •3.2 Механика сплошных сред
- •Тема 4. Основное уравнение вращательного движения. Закон сохранения момента импульса
- •4.1 Динамика вращательного движения
- •4.2. Момент инерции тел правильной геометрической формы относительно неподвижной оси вращения
- •4.3 Момент силы, момент импульса. Основное уравнение динамики вращательного движения
- •Тема 5. Механическая работа. Мощность.
- •Тема 6. Законы сохранения при вращательном движении
- •6.1 Закон сохранения момента импульса. Работа при вращении тела. Кинетическая энергия вращательного движения.
- •Тема 7. Взаимодействие электрических зарядов. Напряженность и потенциал электрического поля
- •7.1.Электрический заряд. Закон Кулона
- •7.2. Напряженность и потенциал электростатического поля,
- •Тема 8. Применение теоремы гаусса к расчету электростатических полей
- •8.1 Поток вектора напряженности электростатического поля (пвэн). Теорема Гаусса
- •Тема 9. Диэктрики, проводники и конденсаторы
- •9.1. Диэлектрики. Электрическое поле в диэлектриках
- •9. 2. Электроемкость проводникoв и конденсаторов
- •8.3 Энергия системы точечных электрических зарядов, заряженных проводников и конденсаторов. Энергия электростатического поля. Объемная плотность энергии. Пондермоторные силы.
- •Тема 10. Постоянный электрический ток
- •10.1. Электрический ток, сила и плотность тока
- •10.2. Электродвижущая сила (эдс). Напряжение
- •10.3. Сопротивление проводников
- •10.4. Последовательное и параллельное соединение проводников
- •10.5. Закон Ома для однородного участка и замкнутой цепи.
- •10.6. Анализ обобщенного закона Ома
- •10.7. Правила Кирхгофа для разветвленных цепей
- •10.8. Работа и мощность тока
- •ТЕма 11. Магнитное поле
- •11.1. Основные характеристики магнитного поля
- •11.2. Закон Био -Савара – Лапласа и его применение
- •11.3. Закон Ампера. Взаимодействие параллельных токов.
- •11.4. Магнитное поле движущегося заряда
- •11.5. Действие магнитного поля на движущийся заряд. Сила Лоренца. Движение заряженных частиц в магнитном поле
- •11.6 Теорема о циркуляции вектора (закон полного тока для магнитного поля в вакууме) и ее применение к расчету магнитных полей
- •Тема 12. Работа в магнитном поле. Явление электромагнитной индукции. Энергия магнитного поля.
- •12.1. Поток вектора магнитной индукции (магнитный поток). Теорема Гаусса для поля
- •12.2 Работа по перемещению проводника и контура с током в магнитном поле
- •12.3. Закон Фарадея (закон электромагнитной индукции). Правило Ленца.
- •12.4. Индуктивность контура. Самоиндукция.
- •12.5 Токи при размыкании и замыкании цепи
- •12.6. Взаимная индукция. Трансформатор
- •12.7. Энергия магнитного поля.
- •12.8 Магнитные свойства вещества. Магнетики
- •12.9 Закон полного тока для магнитного поля в веществе. Циркуляция вектора
- •12.10 Условия на границе раздела двух магнетиков
- •12.11Основы теории Максвелла для электромагнитного поля
- •12.13 Уравнения Максвелла для электромагнитного поля
- •12.14 Следствия из уравнений Максвелла Свойства электромагнитных волн.
- •Тема 13. Механические колебания и волны
- •13.1 Механические колебания
- •13.2. Упругие волны
- •Тема 14. Электромагнитные колебания и волны.
- •14.1 Свободные электромагнитные колебания в идеализированном колебательном контуре
- •Тема 1 5. Законы идеальных газов
- •15.1 Макроскопические состояния
- •9.2 Уравнения состояния идеального газа. Изопроцессы
- •16.1 Идеальный газ как модельная термодинамическая система. Статистические распределения
- •17. Явление переноса в газах
- •17.1 Явления переноса в термодинамически неравновесных системах
- •Тема 18. Основы термодинамики
- •18.1 Внутренняя энергия и работа идеального газа. Первый закон термодинамики и его применение к изопроцессам
- •18.2 Теплоемкость идеального газа
- •18.3 Адиабатический процесс. Уравнение Пуассона
- •18.4 Тепловые двигатели. Цикл Карно и его кпд
- •18.4 Второй закон термодинамики. Неравенство Клаузиуса. Энтропия
Тема 2. Законы динамики. Закон сохранения импульса
2.1. Динамика материальной точки и поступательного движения
твердого тела
Импульс
материальной точки: Импульс
системы материальных точек:
|
Второй
закон Ньютона
(основное уравнение динамики матеpиальной
точки):
Изменение
импульса материальной точки: Δ |
Главный
вектор внешних сил:
=
|
Основной
закон динамики поступательного
движения твердого тела:
|
Радиус-вектор
и координаты центра масс:
x
c=
Закон
движения центра масс:
|
Третий
закон Ньютона:
|
Закон сохранения импульса для замкнутой системы:
где n -число материальных точек (или тел), входящих в систему. |
Пример 3. Автомобиль массой m = 1000 кг движется вверх по наклонной плоскости с уклоном α = 0,1, развивая на пути S = 200 м скорость vк = 54 км/ч. Коэффициент трения μ = 0,05. Определить силу тяги двигателя
Условие:
m =1000 кг;
=1000 кг;
S=200 м;
a=0,1 м/с2;
μ=0,05;
v0 =0;
vк =54км/ч = 15м/с;
F - ?
Решение. Автомобиль движется равноускоренно, причем начальная скорость равна нулю. Выберем ось х, расположенную вдоль наклонной плоскости, ось у – перпендикулярно ей (рис. 3).
На автомобиль действует четыре силы: сила тяжести FТ=mg, сила реакции опоры N, сила тяги F и сила трения FТР. Запишем основной закон динамики:
![]() .
.
Это уравнение в проекциях на оси координат
на ось х ma = F – mg sin - FTP,
на ось у 0 = N – mg cos,
FTP = μ N.
Выразим из этих уравнений силу тяги F
F = mg sin + μmg cos + ma.
Ускорение на этом участке равно:
a = (vk 2 - v02)/(2s) = vk2/(2s).
Найдем силу тяги двигателя на этом участке:
F
= mg
sinα
+ μmg
cosα
+
![]() = m(g
sin
α + μg
cos
α +
= m(g
sin
α + μg
cos
α +
![]() )=
)=
1000(0.98+0,50+0,56) = 2043 Н
ЗАДАНИЕ 3. СИЛЫ ПРИРОДЫ. МЕХАНИКА СПЛОШНЫХ СРЕД
3.1 Фундаментальные взаимодействия в природе. Упругие свойства тел.
Сила
гравитационного взаимодействия:
где m1, m2 – массы взаимодействующих материальных точек, r- расстояние между телами, G=6,67·10-11Н·м2 ·кг-2- гравитационная постоянная. |
Сила
тяжести:
где
на
поверхности Земли:
где M и R - масса и радиус Земли; на высоте h над поверхностью Земли:
на
глубине h
от поверхности Земли:
|
Первая космическая скорость вблизи поверхности Земли:
Первая космическая скорость на высоте h от поверхности Земли:
Вторая
космическая скорость:
|
Вес
тела (сила
реакции опоры): P
= m(g
«+» - ускорение направлено вверх; «—» - ускорение направлено вниз. Невесомость: P = m(g- a) = 0; g=a Коэффициент
перегрузки:
|
Закон Гука для продольного упругого растяжения (сжатия):
где k – коэффициент жесткости, x – смещение, Δl=l-l0 – абсолютное удлинение, lo, l - начальная и конечная длина образца; σ =F/s – нормальное напряжение; s – площадь поперечного сечения образца; ε = Δl/l0 – относительное удлинение; E - модуль Юнга или модуль упругости. |
Сила трения: F = μ N, где μ – κоэффициент трения, N - сила реакции опоры |
Сила сопротивления при движении тела в жидкости и газе соответственно при малых и больших скоростях: F= - β1 v; F = - β2 v2, где β1, β2 - коэффициенты сопротивления движению, v - относительная скорость движения. В
случае турбулентного движения при не
очень больших скоростях лобовое
сопротивление:
где Сх – коэффициент лобового сопротивления, зависящий от формы тела и числа Рейнольдса, S- площадь проекции тела на плоскость, перпендикулярную скорости потока, ρ - плотность среды. Число
Рейнольдса
где l - величина, характеризующая линейные размеры обтекаемого тела |