Расчетно-графическая работа по дисциплине

«Математический анализ»

для студентов ИНЭК (ФГОС ВПО, 2014г.)

(ПИЭН-1, второе высшее образование)

Методические указания по выполнению контрольной работы

.

В соответствии с учебным планом студенты заочного отделения ИНЭК выполняют задания расчетно-графической работы по дисциплине «Математический анализ». Каждый студент выполняет один вариант расчетно-графической работы. Выбор варианта осуществляется по последней цифре в номере зачётной книжки, причем, если номер зачетки оканчивается на 0, то студент выполняет 10-й вариант.

Выполняя контрольную работу, студент должен руководствоваться следующим:

1. Расчетно-графическую работу необходимо сдавать в сроки, установленные графиком учебного процесса.

2. Расчетно-графическую работу следует выполнять в отдельной 12 или 18-ти страничной тетради.

3. К экзамену студент допускается только с зачтенной расчетно-графической работой.

Вопросы для подготовки к экзамену

1. Матрицы и действия над ними.

2. Обратная матрица.

3. Определители и их свойства.

4. Решение систем линейных уравнений методами Крамера и Гаусса.

5. Векторы и действия над ними.

6. Скалярное произведение векторов и его свойства.

7. Уравнения прямой на плоскости (общее, каноническое, проходящей через две точки, параметрическое, с угловым коэффициентом).

8. Понятие функции, область определения.

9. Предел бесконечной числовой последовательности, предел функции.

10. Бесконечно малые и бесконечно большие величины и их свойства.

11. Основные теоремы о пределах. Замечательные пределы.

12. Непрерывность функции в точке и на интервале. Свойства непрерывных функций.

13. Понятие производной функции. Геометрический и физический смысл производной.

14. Основные правила дифференцирования. Таблица производных.

15. Дифференциал функции, его геометрический смысл.

16. Приложения производной к исследованию функций и построению графиков (исследование на интервалы монотонности и точки экстремума, на выпуклость и точки перегиба, на наличие асимптот).

17. Понятие функции нескольких переменных, частные производные, полный дифференциал, экстремум функции нескольких переменных.

18. Неопределенный интеграл и его свойства. Таблица интегралов.

19. Методы интегрирования некоторых классов функций.

20. Понятие определенного интеграла. Формула Ньютона-Лейбница. Основные свойства определенного интеграла.

21. Приложения определенного интеграла к решению геометрических и других задач.

22. Дифференциальные уравнения 1-го порядка. Общее и частное решение, задача Коши. Дифференциальные уравнения с разделяющимися переменными.

23. Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.

24. Числовой ряд, сумма ряда, сходящиеся и расходящиеся ряды. Свойства числовых рядов.

25. Необходимый признак сходимости числового ряда. Достаточные признаки сходимости: предельный признак сравнения, признак Даламбера, признак Коши, интегральный признак Коши.

26. Знакочередующиеся ряды. Абсолютная и условная сходимости. Признак Лейбница.

27. Функциональные ряды. Область сходимости функционального ряда.

28. Степенные ряды. Теорема Абеля. Вычисление радиуса сходимости R и области сходимости степенного ряда. Свойства степенных рядов.

Рекомендуемая литература

1. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М., 1995.

2. Щипачев В.С. Высшая математика. М., 2001.

3. Высшая математика для экономистов. Под редакцией Кремера Н.Ш., М., 1997.

4. Сборник задач по высшей математике для экономистов. Под редакцией Ермакова В.И. М., 2002.

Задания расчетно-графической работы

Задание 1.

Найти: а) обратную матрицу . Проверить равенство ;

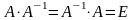б) матрицу , где получается из ее транспонированием

Вариант	Матрица	Вариант	Матрица
1.		2.
3.		4.
5.		6.
7.		8.
9.		10.

Задание 2. Решить системы уравнений по правилу Крамера.

№ варианта	Исходные данные
1
2
3
4
5
6
7
8
9
10

Задание 3.

Решить системы методом Гаусса. Записать общее решение системы и два частных решения.

Вариант	Система	Вариант	Система
1.		2.
3.		4.
5.		6.
7.		8.
9.		10.

Задание 4.

Даны координаты вершин треугольника ABC. Найти: длины сторон треугольника ABC; 2) внутренние углы данного треугольника; 3) длину медианы AE; 4) уравнения сторон AB, BC, CA (общее, каноническое, проходящей через две точки, параметрическое, с угловым коэффициентом). Сделать чертеж.

№ варианта	Исходные данные
1	A( 4 ; 0 ), B( 7 ; 4 ), C( 8 ; 2 )
2	A( 2 ; 2 ), B( 5 ; 6 ), C( 6 ; 4 )
3	A( 0 ; 2 ), B( 3 ; 6 ), C( 4 ; 4 )
4	A( 4 ; 1 ), B( 7 ; 5 ), C( 8 ; 3 )
5	A( 3 ; 2 ), B( 6 ; 6 ), C( 7 ; 4 )
6	A(-2 ; 1 ), B( 1 ; 5 ), C( 2 ; 3 )
7	A( 4 ; -3), B( 7 ; 1 ), C( 8 ;-1 )
8	A(-2 ; 2 ), B( 1 ; 6 ), C( 2 ; 4 )
9	A( 5 ; 0 ), B( 8 ; 4 ), C( 9 ; 2 )
10	A( 2 ; 3 ), B( 5 ; 7 ), C( 6 ; 5 )

Задание 5.

Найти пределы данных функций:

вариант
	а) . б)
	а) б)
	а) б)
	а) б)
	а) б)
	а) б)
	а) б)
	а) б)
	а) б)
	а) б)

Задание 6.

Найти производные заданных функций:

Вариант	Функция
1.	а)	б)
	в)	г)
2.	а)	б)
	в)	г)
3.	а)	б)
	в)	г)
4.	а)	б)
	в)	г)
5.	а)	б)
	в)	г)
6.	а)	б)
	в)	г)
7.	а)	б)
	в)	г)
8.	а)	б)
	в)	г)
9.	а)	б)
	в)	г)
10.	а)	б)
	в)	г)

Задание 7.

Исследовать методами дифференциального исчисления функции и, используя результаты исследования, построить графики данных функций по следующей схеме:

• найти область определения функции;

• исследовать на четность, нечетность, периодичность;

• найти точки пересечения графика функции с осями координат;

• исследовать функцию на непрерывность, найти точки разрыва функции и ее односторонние пределы в точках разрыва;

• найти точки экстремума и интервалы ее монотонности;

• найти точки перегиба, интервалы выпуклости и вогнутости графика функции;

• найти асимптоты графика, используя результаты предыдущих исследований.

1. а) ; б) .

2. а) ; б) .

3. а) ; б) .

4. а) ; б) .

5. а) ; б) .

6. а) ; б) .

7. а) ; б) .

8. а) ; б) .

9. а) ; б) .

10. а) ; б)

Задание 8.

Вычислить частные производные и полные дифференциалы от заданных функций:

вариант
	а) б)
	а) б)
	а) б)
	а) б)
	а) б)
	а) б)
	а) б)
	а) б)
	а) б)
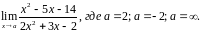	а) б)