Пример №8

Рассмотрим двухканальную СМО. Пусть транспортное подразделение в карьере обслуживают два экскаватора, каждый из которых с определенной вероятностью может выйти из строя. Отказавший экскаватор сразу же начинают ремонтировать. По окончанию ремонта он немедленно включается в процесс погрузки. СМО, описывающая эту производственную ситуацию, имеет четыре состояния.

λ₂

µ₁

λ₂

µ₂

λ₁

µ₂

λ₁

µ₁

Рис.2 Граф состояний СМО

• S₁ - оба экскаватора (аппарата обслуживания) работают;

• S₂ - первый экскаватор находится в ремонте, второй осуществляет погрузку;

• S₃ - первый экскаватор работает, второй находится в ремонте;

• S₄ - оба экскаватора находятся в ремонте.

Переходы S₁→S₂, S₁→S₃, S₂→S₄, и S₃→S₄ обусловлены отказами в работе экскаваторов с интенсивностями; λ₁ – плотность потока отказов первого экскаватора; λ₂- плотность потока отказов второго экскаватора.

Обратные переходы S₂→S₁, S₃→S₁, S₄→S₂, и S₄→S₃ являются следствием выполненных ремонтов; при этом µ₁, µ₂ – пропускные способности после завершения ремонта соответственно первого и второго экскаваторов.

Для графа состояний можно записать уравнение Колмогорова (соответственно для состояний S₁,S₂, S₃, S₄):

(λ₁+λ₂) p₁=µ₁ p₂+ µ₂ p₃ ;

(λ₂+µ₁) p₂=λ₁ p₁+ µ₂ p₄ ;

(λ₁+µ₂) p₃=λ₂ p₁+ µ₁ p₄ ;

(µ₁+µ₂) p₄=λ₂ p₂+ λ₁ p₃ ,

где p₁, p₂, p₃, p₄ – вероятности состояний соответственно S₁,S₂, S₃, S₄ .

Используя нормировочное условие p₁+ p₂+p₃+ p₄=1, при конкретных значениях λ и µ можно решить систему уравнений относительно p.

В карьере работают два экскаватора, характеристики которых приведены в таблице. Определить размер месячной отгрузки материала при среднем числе рабочих дней, равном 24.

Номер экскаватора	Производительность Пэ, м3/смена	Число поломок в месяц i	Число ремонтов, которые можно провести в месяц, i
1	700	1	2
2	475	2	3

С учетом значений λ_i и µ_i , указанных в таблице запишем систему уравнений

p₁+ p₂+p₃+ p₄=1

Решив ее, получим р₁=0,4, р₂=0,2, р₃=0,27, р₄=0,13. Вероятность р₁=0,4 означает, что 40% времени оба экскаватора будут работать совместно на погрузке; р₂=0,2 - 20% времени первый экскаватор будет в работе, а второй в ремонте; р₃=0,27 - 27% времени первый экскаватор будет в ремонте, а второй на погрузке; р₄=0,13 – 13% времени погрузочные работы будут приостановлены из-за одновременной неисправности обоих экскаваторов.

При условии полного обеспечения транспортными средствами карьер ежемесячно способен отгрузить

Математическое ожидание ежесуточно отгружаемого материала составляет 18096 ÷ 24 =754 м³.

Пример №9

Обосновать целесообразность замены второго экскаватора на новый производительностью 500 м³ в смену, имеющий меньшую трудоемкость ремонта (в течение месяца можно провести пять ремонтов) и в два раза меньшую по сравнению с заменяемым экскаватором частоту отказов (одна поломка в месяц).

Номер экскаватора	Производительность Пэ, м3/смена	Число поломок в месяц i	Число ремонтов, которые можно провести в месяц, i
1	700	1	2
2	500	1	5

Составим систему уравнений Колмогорова:

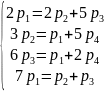
р₁+р₂+р₃+р₄=1.

Решив ее, получим р₁=0,56, р₂=0,278 р₃=0,111, р₄=0,051.

Анализ вероятностей состояния СМО показывает, что замена второго экскаватора на новый вдвое снизила вероятность простоя обоих экскаваторов одновременно, повысила вероятность исправной работы этих экскаваторов и вдвое уменьшила вероятность нахождения в ремонте второго экскаватора.

Несмотря на то, что новый экскаватор имеет производительность всего на 25 м³/смена больше заменяемого (примерно на 5%), перераспределение вероятностей состояния приводит к более значительному увеличению объема сменной погрузки материала в карьере, который составляет

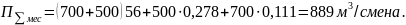
Полученный результат на 18% выше, чем в предыдущем примере

Следовательно, замена второго экскаватора целесообразна.