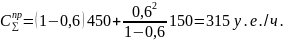Пример №6

Определить основные параметры работы заготовительно-транспортного подразделения в составе одного экскаватора и пяти самосвалов, если производительность экскаватора 50м³/ч, объем кузова самосвала 5м³, время рейса самосвала 1ч. Пусть S₀-экскаватор простаивает, S₁-экскаватор осуществляет погрузку.

В данном случае имеем одноканальную СМО с отказом. Пропускная способность аппарата обслуживания μ=50/5=10авт./ч, λ=50/10=5авт./ч. Состояние системы описываются графом состояний, показанном на Рис.1

λ

μ

Рис.1 Граф состояний

Из состояния S₀ в состояние S₁ систему переводит поток автомобилей с пропускной способностью λ=5; из S₁ в S₀- «поток обслуживаний» с пропускной способностью μ=10. Вероятность простоя экскаватора в любой момент времени t составляет P₀(t), а вероятность нахождения на погрузке - P₁(t). Совокупность обоих состояний S₀ и S₁ образует полную систему, следовательно:

P₀(t) + P₁(t) = 1

Составим для графа уравнение Колмогорова:

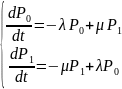
Следует простое правило записи уравнений Колмогорова для любого графа состояний, описывающего возможные переходы из любого состояния S₁ в состояния S_j, S_k и т.п. оно сводится к трем положениям:

1. В любой части уравнения стоит производная вероятности состояния по времени; правая содержит столько слагаемых, сколько стрелок связано с данным состоянием

2. Если стрелка направлена из состояния S_i, то это слагаемое имеет знак «минус» и равно произведению плотности вероятности перехода из состояния S_i и вероятности такого перехода P_i

3. Если стрелка направлена в состояние S_j, то это слагаемое имеет знак «плюс» и является произведением плотности вероятности перехода в состояние S_j и вероятности такого перехода P_j

Решив систему уравнений получим:

,

,

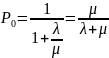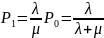В нашем примере

,

.

Это свидетельствует о том, что система недостаточно эффективна: высокая вероятность простоя экскаватора снижает количество отгружаемого в смену материала с 50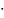 8= 400 м³ до 400 0,33=132 м³ . Потери от простоев достигают 400 0,67= 268 м³/ в смену.

Кроме потери производительности на вывозке материала из карьера строительная организация будет нести убытки от простоя экскаватора. Поэтому необходимо либо поставить в карьер менее производительный экскаватор (это минимизирует его потери от простоя), либо увеличить число самосвалов (это повысит объем вывозимого материала и снизит вероятность простоя экскаватора).

Допустим, плотность потока самосвалов увеличили второе (λ=15). Тогда,

,

.

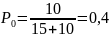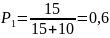В результате объем транспортных работ увеличится до 240 м³ в смену, а потери снизится до 160 м³ /в смену.

Пример №7

Рассчитать оптимальный состав заготовительно - транспортного подразделения при котором суммарные потери от простоев техники будут наименьшими. стоимость простоя экскаватора составляет 450 у.е, а самосвалов 150 у.е. Остальные условия также как в примере первом.

Обозначив суммарные потери от простоев техники 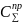, потери простоя экскаватора 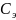, а от простоя самосвала 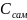, запишем целевую функцию

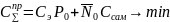
где вероятность простоя эскалатора, 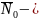среднее число самосвалов в очереди на обслуживание (погрузку).

Естественно, что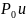 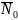являются функциями параметров СМО λ и μ.

Выражение можно сформулировать так: неважно из-за каких простоев имеют место потери, наша цель сделать эти суммарные потери минимальными.

В теории массового обслуживания доказано, что в разомкнутых СМО средние числа требований в системе 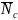и в очереди зависят от интенсивности обслуживания 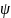и описываются зависимостями:

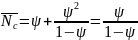
или

,

.

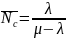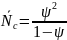Выражение справедливо для всего периода функционирования системы. Для того времени, когда существует очередь, оно принимает вид

.

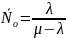Для данного периода более простой будет зависимость для p₀ . Если принять за вероятность наличия процесса обслуживания показатель , то вероятность простоя экскаватора p₀ есть вероятность противоположного события:

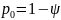
Целевая функция принимает вид

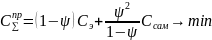
Отсюда можно найти значение оптимальной интенсивности обслуживания 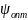, т.е. суммарные потери от простоев техники будут минимальными. Для этого нужно продифференцировать по , приравнять производную нулю, и решить полученное уравнение относительно .

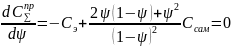
В результате получим

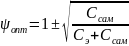
В результате нашего примера получим

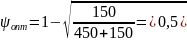
Поскольку 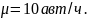, , 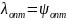. При времени рейса 1 час число автомобилей, закрепленных за экскаватором, должно быть равным 5. При этом суммарные потери от простоев составят:

.

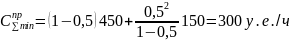Чтобы убедиться, что эти потери минимально возможные, изменим число самосвалов в большую или меньшую сторону от оптимального.

При

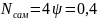
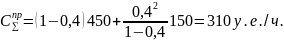
При