Пример №5

Требуется определить рациональный радиус действия асфальтобетонного завода (АБЗ) исходя из условия обеспечения минимальной стоимости 1 м² асфальтобетонного покрытия.

Для решения задачи примем следующие обозначения:

R_a - протяженность участка дороги, обеспечиваемая асфальтобетонной смесью с одного месторасположения АБЗ (радиус действия завода), км;

C_n – стоимость перемещения АБЗ, отнесенная к 1 м² готового асфальтобетонного покрытия, тыс. руб./м²;

C_тр – затраты на транспортирование асфальтобетонной смеси на расстояние Ra/2 в количестве, необходимом для устройства 1 м² покрытия, тыс. руб./м²;

С_д.м. – суммарная стоимость демонтажа и монтажа оборудования завода, тыс. руб.;

Q_АБЗ – масса оборудования АБЗ, т.

Если тип АБЗ известен, то математическая постановка задачи определения оптимального радиуса действия завода может быть выражена зависимостью

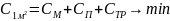
Стоимость материалов С_м не зависит от R_a.

Стоимость перемещения завода на новое место можно описать выражением

,

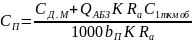где К- коэффициент, зависящий от расчетной схемы работы АБЗ, К=1 и К=2, С_{1ткм об} – стоимость одного тонно-километра перевозки оборудования АБЗ; b_n – ширина дорожного асфальтобетонного покрытия, м.

Средняя стоимость транспортирования асфальтобетонной смеси, необходимой для устройства 1 м² покрытия.

,

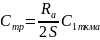где С_1ткма – стоимость одного тонно-километра перевозки асфальтобетонной смеси, тыс. руб./(т ^. км); S – площадь покрытия, которая может быть устроена из 1 т асфальтобетонной смеси, м²/т.

Продифференцируем полученную зависимость по переменной R_a и приравняем нулю:

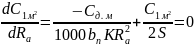
Решив уравнение относительно R_a, получим

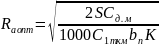
Допустим, в рассматриваемом примере С_д.м =12,5 млн руб.; S =4 м²/т; b_n =7,5 м; К=1; С_1ткм = 0,02 тыс. руб.

Подставив исходные данные в формулу, получим

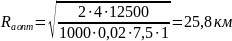
Если принять для расчета (К=2), то получим

.

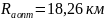4. Применение моделей массового обслуживания в проектировании производства работ

4.1. Основные положения теории массового обслуживания. Классификация моделей массового обслуживания

СМО - совокупность функционально связанных элементов, ориентированных на достижение определенной цели (или группы целей).

СМО может быть представлена следующими тремя элементами:

1. Аппарат (прибор) обслуживания;

2. Поток требований на обслуживание (входящий поток);

3. Поток обслуживания требований (исходящий поток).

Аппарат обслуживания называют прибором, или каналом, обслуживания. В связи с этим СМО подразделяются на одноканальные и многоканальные. Поток требований на обслуживание называют потоком заявок.

Каждый из элементов системы оценивается собственными характеристиками.

Характеристикой аппарата (канала) обслуживания является его пропускная способность. µ- число требований (заявок), обслуживаемых в единицу времени.

Поток требований характеризуется плотностью потока λ – средним числом требований, прибывающих в единицу времени на обслуживание.

Отношение плотности потока к пропускной способности аппарата обслуживания называется интенсивностью обслуживания.

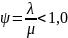
Этот показатель может быть меньше, равен или больше единицы, однако ТМО рассматривает только условие 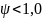(в противном случае имеет место спонтанный рост очереди, модели массового обслуживания эту ситуацию не описывают).

Предметом ТМО является установление зависимости между характером потока заявок (требований) на обслуживание, числом каналов и их пропускной способностью, правилами организации СМО и эффективностью обслуживания.

Показателями эффективности обслуживания являются:

- Среднее число заявок, которое система может обслужить за единицу времени;

- Средняя доля ( или процент) необслуженных заявок, покинувших систему;

- Среднее время ожидания в очереди;

- Среднее время нахождения заявки в системе (то есть с учетом времени ожидания в очереди и продолжительности обслуживания);

- Среднее число заявок находящихся в системе;

- Относительная и абсолютная пропускные способности СМО.

Относительная пропускная способность СМО q определяет вероятность того, что в момент поступления заявки на обслуживание канал свободен, и она будет обслужена. Для одноканальной системы q=P₀ , где P₀ – вероятность того, что канал свободен.

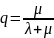
Абсолютная пропускная способность СМО А есть произведение относительной пропускной способности на интенсивность потока.

Важнейшими показателями СМО являются:

1. Вероятность того, что канал обслуживания свободен и поступающая заявка будет обслужена (P₀);

2. Вероятность того, что в момент поступления заявки канал обслуживания занят (СМО занято) и заявка должна либо ожидать, либо покинуть систему (P₁);

3. Вероятность отказа