Пример №3

На заводе строительных конструкций было принято решение выпустить новую балку перекрытия, работающую в условиях динамического нагружения. Для проверки ее работоспособности были изготовлены 78 образцов, которые проверялись путем динамического нагружения до появления усталостных трещин. Результат испытаний приведен в таблице

Результат испытаний образцов

Число нагружений до появления трещин xi	30	40	50	60	70	80	90	100	110	120
Число испытаний ni, в которых появилась трещина	2	6	10	12	18	10	8	6	4	2

Данные таблицы показывают, что в двух случаях трещины появились после 30 нагружений, в шести случаях – после 40 нагружений и т.п. для удобства расчетов и отображения данных показателей значений x_i разбиты на интервалы по 10 испытаний. Всего интервалов девять. Проверим достаточно ли такого числа интервалов.

Согласно формулам

,

,

.

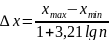оптимальная длина интервала 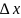и число интервалов К равны:

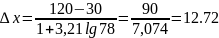
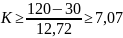
Согласно зависимости К ≥6. Следовательно, число интервалов в таблице К=10 вполне достаточно.

Пример №4

Определить достаточность статистической выборки для исследования работоспособности строительных конструкций с надежностью 0,9 (результаты статистических испытаний приведены в таблице)78 образцов

Результат испытаний образцов

Число нагружений до появления трещин xi	30	40	50	60	70	80	90	100	110	120
Число испытаний ni, в которых появилась трещина	2	6	10	12	18	10	8	6	4	2

Чтобы воспользоваться неравенством Чебышева, определим характеристики выборки 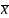и D(x) по формулам теории вероятностей

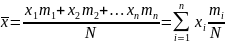
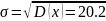
При =71,5 показатель =0,1 =7,15

Подставив полученные значения в неравенство Чебышева, будем иметь

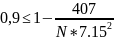
Решив неравенство относительно N, получим N . Имеющийся объем выборки N=78 измерений отличается от требуемого на два измерения, т.е. менее чем на 3%, следовательно, выборку можно считать достаточной.

3. Модели экстремального анализа в проектировании дорожного строительства

3.1. Общая постановка задачи экстремального анализа в дорожном строительстве

В транспортном строительстве целью экстремального анализа является минимизация финансовых или материальных затрат, сроков строительства, простоев техники либо максимизация прибыли, темпов строительства, уровня рентабельности производства и т.п.

Поиск экстремального значения какого-либо процесса, установление динамики показателей производственной деятельности могут осуществляться различными методами, например методами математической статистики, статистического прогнозирования, дифференциального исчисления и др.

Рассмотрим наиболее распространенные классы задач, решаемых методами экстремального анализа.

1. При формировании комплексных подразделений часто возникает задача равномерной загрузки техники, минимизации потерь от простоев машин. Подобную ситуацию можно проследить на примере комплектования заготовительно-транспортного подразделения, предназначенного для погрузки и транспортирования песка из карьера на объект строительства.

Постановка задачи экстремального анализа может быть сформулирована следующим образом: независимо от того, за счет каких простоев строительная организация будет нести потери, суммарные потери должны быть минимальными.

2. При расчете оптимального темпа строительства транспортных объектов приходится решать двойственную задачу. Низкий темп работ требует меньших затрат на строительные машины и заработную плату рабочих (за счет их численности), но создает риск несвоевременного завершения строительства и применения заказчиком штрафных санкций. Наоборот, привлечение дорогостоящей техники (или увеличение ее численности) повышает стоимость строительства, но уменьшает риск штрафных санкций. Более того, досрочная сдача объекта в эксплуатацию дает экономический эффект (дополнительную прибыль). Отсюда задача выбора оптимального темпа строительства сводится к нахождению такого темпа работ, при котором суммарные издержки строительной организации от уплаты штрафов в дополнительных затрат на строительство будут минимальными. (Рис.3.2.)

Математическая постановка задачи представляет собой целевую функцию, в которой минимизируются общие издержки строительной организации 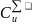, представляющие собой сумму затрат на обеспечение принятого темпа работ С_V и штрафов за несвоевременную сдачу объекта С_ш.

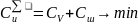
3. Обеспечение строительства материалами и конструкциями требует создания производственных запасов. Повышенные запасы гарантируют ритмичность строительства, но требует больших затрат на создание и эксплуатацию складского хозяйства. В тоже время при повышенных запасах становятся меньше расходы на их создание, поскольку крупная разовая поставка материалов дешевле, чем частые поставки мелкими партиями. Здесь имеет место та же принципиальная постановка задачи, в которой целевая функция представляет собой сумму частных функций

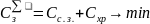
гд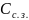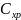е, , – затраты соответственно на создание запасов и их хранение.

Приведенные задачи не исчерпывают всего многообразия экономических ситуаций в транспортном строительстве, оптимизируемых с помощью методов экстремального анализа. Наиболее сложным моментом в решении задач с использованием экстремального анализа является построение математической модели (целевой функции), которую предстоит дифференцировать. Все дальнейшее сводится к выполнению обычной вычислительной процедуры классической математики.