Пример №2

При строительстве дороги применяется экскаватор нового типа, нормы выработки которого отсутствуют. Для обоснования этой нормы проведено 100 натуральных измерений выработки машины при выполнении земляных работ. Данные измерений (ряд распределения) приведены в таблице

Ряд распределения выработки экскаватора

Производительность экскаватора xi, м3/ч	30..40	40..50	50..60	60..70	70..80	80..90	90..100	100..110
Число случаев mi	0	4	24	40	20	10	2	0

Построим гистограмму распределения выработки, откладывая по оси абсцисс интервалы значений x_i , а по оси ординат – число наблюдений m_i.

Гистограмма -  способ графического представления табличных данных. Количественные соотношения некоторого показателя представлены в виде прямоугольников, площади которых пропорциональны. Чаще всего для удобства восприятия ширину прямоугольников берут одинаковую, при этом их высота определяет соотношения отображаемого параметра.

Найдем величину эмпирического среднего

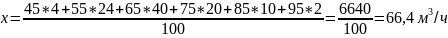
Рассчитаем дисперсию и среднее квадратическое отклонение:

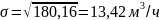
Определим коэффициент вариации:

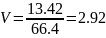
Рассчитанные числовые характеристики дают определенную информацию о вероятностном процессе производительности экскаватора. Например, среднее значение 66,4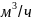 может быть принято в качестве часовой нормы выработки машины, однако из гистограммы видно, что от этой нормы имеются существенные отклонения (в пределах от 40 до 100 ). Поэтому неясно, насколько достоверным будет этот норматив, с какой вероятностью он будет отражать реальный производительный процесс. Для ответа на эти вопросы необходимо установить закон распределения случайной величины.

2.2. Элементы математической статистики. Статистическая проверка гипотез

Математическая статистика - это раздел математики, посвящённый математическим методам систематизации, обработки и использования статистических данных для научных и практических выводов.

В задачу математической статистики входит изучение массовых явлений в природе, технике, производстве, обществе. Везде, где приходится иметь дело с обработкой экспериментальных или иных массовых результатов, пользуются методами математической статистики.

Метод исследования, опирающийся на рассмотрение статистических данных о тех или иных совокупностях объектов, называется статистическим.

Общие черты статистического метода:

• Подсчет числа объектов (параметров), входящих в исследуемую группу;

• Анализ распределения количественных признаков;

• Применение выборочного метода, когда детальное исследование всей обширной совокупности затруднено;

• Использование теории вероятностей при оценке параметров распределения статистической выборки;

• Оценка достаточности числа наблюдений для достижения заданной достоверности результата.

Важнейшим элементом математической статистики является обработка статистических данных, включающая в себя построение статистического ряда (гистограммы), вычисление статистических характеристик, установление закона распределения, которым может быть описана случайная величина, формулирование выводов.

Важным элементом построения гистограммы- определение числа интервалов, на которые разбивается весь диапазон статистического ряда. Существует несколько методик решения этой задачи.

Одна из них основана на расчете оптимальной длины интервала с последующим определением числа интервалов.

Оптимальная длина интервала рассчитывается по формуле

,

где 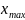, 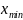-максимльное и минимальное значения статистического ряда (границы диапазона) , n-объем выборки.

Число интервалов

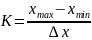
Если К – число дробное, то за число интервалов принимается ближайшее целое число, большее К.

Другая методика предполагает определение числа интервалов по формуле

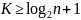
Эта формула, позволяющая получить нижнюю границу (наименьшее значение) К, наиболее точна при больших значениях n. Например, при n=100 К≥6, а при n=1000 К≥9.

Другим важным вопросом, решаемым при статистической обработке данных, является доказательство достаточности объема выработки (числа опытов). Для этого можно воспользоваться неравенством Чебышева:

,

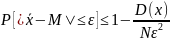где 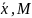- соответственно статистическое среднее и математическое ожидание изучаемой случайной величины; 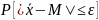- вероятность того, что разность 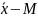не превысит некоторого заданного числа 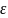, называемого точность измерения ( принимают равным 5 или 10% от величины ); D(x) – дисперсия статической выработки из N измерений.