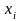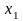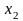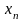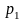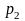Пример №1

Для рытья котлована объемом 1080м³ строители получили 3 экскаватора. Первый экскаватор имеет производительность 22,5м³/час и расходует в час 12 литров топлива. Второй экскаватор 10м³/час, 10 литров /час. Третий - 5 м³/час, 2 литра/час. Экскаваторы могут работать совместно, не мешая друг другу. Запас топлива ограничен и равен 4600 м³. Требуется как можно скорее разработать выемку котлована.

Необходимо составить математическую модель данной задачи.

Решение:

1. Введем переменные: x_i - время работы i-го экскаватора (i=1,2,3) х₄ – время рытья котлована

2. Целевая функция: z=x₄ ( min)

3. Составляем равенство. Нужно разработать весь объем котлована.

22,5x₁+10x₂+5x₃=1080

4. Составляем ограничения.

12x₁+10x₂+2x₃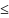 4600 – ограничение на топливо;

0 x₁ x₄ – время работы первого экскаватора;

0 x₂ x₄ – время работы второго экскаватора;

0 x₃ x₄ – время работы третьего экскаватора.

2. Прикладные вопросы теории вероятностей и математической статистики в проектировании автомобильных дорог

Экономико-математические модели подразделяют на детерминированные и вероятностные. В строительном производстве детерминированные процессы встречаются крайне редко. Поскольку овладение вероятностными моделями, как и вероятностными расчетами вообще, для инженера, менеджера, экономиста является весьма важным. Необходимо усвоить основные термины (понятия) теории вероятностей, законы распределения случайных величин, их основные характеристики, а также методы выполнения вероятностных расчетов и оценки их точности.

К наиболее важным в теории вероятностей относятся понятия «событие», «группа событий», «случайная величина», «вероятность события».

Событием называется факт, который в конкретных условиях (в результате опыта) может произойти либо не произойти. Примерами событий являются нормальная работа или отказ машины, оборудования, своевременная или с опозданием сдача объекта в эксплуатацию, наличие или отсутствие затора машин на дороге и т.п.

Группа событий включает в себя те события, хотя бы одно из которых должно произойти при реализации заданного комплекса условий. Сумма таких событий А и В представляет собой достоверное событие

Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать

Вероятностью события называется возможность (шанс) осуществления этого события в ходе случайного эксперимента.

 

2.1. Закон распределения случайной величины

Случайные величины бывают дискретные и непрерывные. Любая случайная величина описывается законом распределения.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения может иметь разные формы.

Рядом распределения дискретной случайной величины Х называется таблица, где перечислены возможные (различные) значения этой случайной величины х₁, х₂, ..., х_n с соответствующими им вероятностями р₁, р₂, ..., р_n ( ):

			…
			…

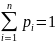В теории вероятности важную роль играет другая функция – плотность распределения случайной величины f(x) – предел отношения вероятность попадания случайной величины Х на малый участок ∆x к длине этого участка при не ограниченном ее уменьшении.

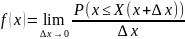
1. Вероятность попадания х на участок [a,b] при функции распределения вычисляется по зависимости P(a ≤ x ≤ b)=F(b)-F(a)

2. Если F(+∞)=1, 0, то 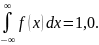Данный интервал отражает вероятность достоверного события попадания случайной величины на участок от -∞ до +∞, равную единице.

3. Плотность распределения есть производная от функции распределения, и наоборот

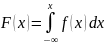
Величину F(x) принято называть интегральной функцией распределения, а f(x)- дифференциальной функцией распределения случайной величины Х.

Этих двух функций недостаточно для полной математической определенности закона распределения. Для этого нужно знать числовые характеристики закона распределения: эмпирическое среднее (математическое ожидание); дисперсию, среднее квадратическое отклонение; коэффициент вариации.

Эмпирическое среднее 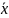- величина, относительно которой группируются, рассеиваются все возможные значения случайной величины.

,

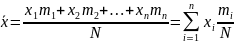где 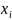– возможные значения случайной величины Х, 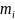– число случаев появления значений из N проведенных опытов (наблюдений).

Математическое ожидание M(x) является теоретической характеристикой случайной величины, к которой стремится эмпирическое среднее при увеличении числа наблюдений

,

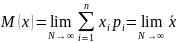где 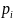– частота значений при N наблюдениях, .

Дисперсия D(x) является характеристикой степени рассеивания случайной величины относительно или M(x). Она определяется по формуле

или

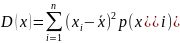
Для малых выборок (число измерений N <30…40) дисперсия вычисляется по формуле

,

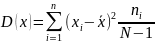Среднее квадратическое отклонение σ, представляющее собой квадратный корень дисперсии

,

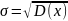Коэффициент вариации рассчитывается по формуле