7.3. Сетевое планирование в условиях неопределенности

Продолжительность выполнения работ часто трудно задать точно и потому в практической работе вместо одного числа задаются 2 оценки – минимальная и максимальная.

Минимальная (оптимистическая) оценка t_min(i,j) характеризует продолжительность выполенния работы при наиболее благоприятных обстоятельствах. Максимальная (пессимистическая) t_max(i,j) – при наиболее неблагоприятных. Продолжительность работы в этом случае рассматривается как случайная величина, которая в результате реализации может принять любое значение в заданном интервале.

Такие оценки называют вероятностными (случайными) и считают, что они подчинятся β – распределения. В этом случае ожидаемое значение продолжительности работ (среднее значение)

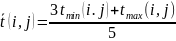
Степень разброса возможных значений t(i,j) вокруг t_ож(i,j) может быть охарактеризовано дисперсией:

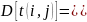
При достаточно большом количестве работ можно утверждать, что общая продолжительность любого пути, в том числе и критического имеет нормальный закон распределения. Это утверждение применяется в соответствии с законом больших чисел, который звучит так:

Путь х₁, х₂, … х_n – случайные величины, подчиняющиеся различным законам распределения. Тогда, при достаточно большом значении n случайная величина

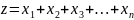
Будет подчиняться нормальному закону распределения, причем

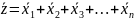
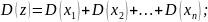
Где 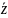, , …, 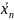средние значения случайных величин

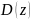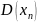, , …, - дисперсии этих величин

Вспомни, что среднеквадратическое отклонение случайной величины равна квадратному корню из дисперсии.

Где L – длина пути;

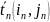- среднее значение пути между событиями

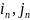
Дисперсия пути

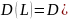
При вероятностной постановке задачи, кроме обычных характеристик сетевой модели, можно решить две дополнительные задачи.

Первая задача. Определить вероятность того, что продолжительность критического пути t_кр не превысит заданного директивного уровня Т.

Данная задача легко решится

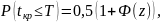
Здесь - вероятность того, что продолжительность критического пути 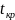не превысит заданного директивного уровня Т;

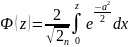-функция Лапласа,

Применяема по специальным таблицам

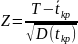
Или

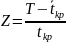
Где 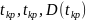- соответственно среднее значение, среднеквадратическое отклонение от среднего и дисперсии случайной величины .

Если значение вероятности 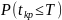достаточно велико (более 0.8), то можно с высокой степенью уверенности предполагать своевременность выполнения всего комплекса работ.

Вторая задача. Определить максимальный срок выполнения всего комплекса работ Т при заданном уровне вероятности p. Здесь 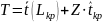где z- это аргумент функции Лапласа Ф(Z).

Сначала вычисляем используя

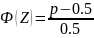
Затем по таблице находим Z. И по формуле вычисляем Т.

Пример №3

Структура сетевой модели и оценка продолжительности работ (в сутки) заданы в таблице.

Работа (i,j)	Продолжительность		Ожидаемая продолжительность		Дисперсия
	tmin(i,j)	tmax(i,j)
(1,2)	5	7,5		6		0,25
(2,3)	4	6,5		5		0,25
(2,4)	3	6		4		0,36
(2,5)	1	5,5		3		0,81
(3,7)	0,5	3,5		2		0,36
(4,5)	5	7,5		6		0,25
(4,6)	3	5,5		4		0,25
(4,9)	5	10		7		1,00
(5,8)	2	4,5		3		0,25
(5,10)	7	12		9		1,00
(6,9)	0	0		0		0,00
(6,11)	3	8		5		1,00
(7,10)	4	9		6		1,00
(8,10)	2	7		4		1,00
(9,10)	1	6		3		1,00
(10,11)	8	10,5		9		0,25

1. Вычислим определённую продолжительность по формуле (1)

2. Вычислим дисперсию по формуле (2).

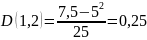
3. Найдём критический путь. Для этого сначала построим график. И укажем ожидаемые продолжительности пути.

4. Вычислим критический путь 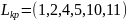. Его продолжительность

5. Дисперсия критического пути.

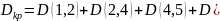
6. Среднеквадратическое отклонение

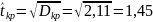
7. Найдём вероятность выполнения всего комплекса работ за 35 дней

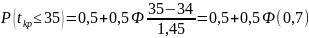
По таблицам

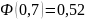
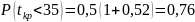
8. Найдём вероятность выполнения всего комплекса работ за 30 дней.

Из свойств функции Лапласа следует, что 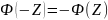. Тогда

.

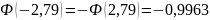9. Решаем обратную задачу. Определяем максимально возможный срок выполнения всего комплекса работ с вероятностью Ф=0.95

Найдём функцию Лапласа

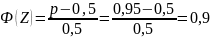
По таблице при 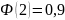Z=1,7 Тогда получаем T=34+1,7 1,45=36,46 сут. Это максимальный срок выполнения всего комплекса работ при P=95%.