7.1 Основные понятия сетевой модели.

1. Событие – это результаты выполнения одной или несколько работ. Они не имеют протяженности во времени. События совершаются в тот момент, когда оканчивается последняя из работ, входящая в него. При графическом представлении события изображаются графом, когда события изображаются кружком (или иной геометрической фигурой), внутри которого представляется его порядковый номер (I=1,2….n).

В сетевой модели имеется начальное событие (с номером 1), из которого работы только выходят, и конечное событие (с номером N), в которых работы только входят.

На рисунке изображена модель с 10 работами. Начальная работа 1, конечная – 10.

Рис. – График двух конечных множеств

2. Работа характеризует материальное действие, требующее модель взаимосвязи событий.

При графическом представлении работа изображается стрелкой, которая соединяет 2 события. Она обозначается парой заключенных в скобки чисел (i,j), гдеi-номер события, из которого работа выходит, а j-номер события, в которое оно входит.

Работа не может начаться раньше, чем свершится событие, из которого она выходит.

Каждая работа имеет определенную продолжительность t(i,j). Например, запись t(2,5)=4 означает, что работа (2,5) имеет продолжительность 4 единицы.

7.2. Основные требования к сетевой модели

1. События должны быть правильно пронумерованными, то есть для каждой работ (i,j) i<j.

2. Отсутствует тупиковые события (кроме завершающего), из которого нет выхода.

3. Отсутствуют события (за исключением исходного), которым не предшествует хотя бы одна работа.

4. Отсутствуют циклы, то есть замкнутые пути, соединяющие события с ним же самим.

Пример №13

Найти ошибки при построении сетевой модели, приведенной на рисунке

`

Рис. – Сетевая модель

1-ая ошибка: неправильно пронумерованы вершины 2 и 3, так как имеет место работа (3,2);

2-ая ошибка: присутствуют тупиковые события (5);

3-ая ошибка: присутствует событие 7, которому не предшествует ни какая работа;

4-ая ошибка: имеет место цикл: (2,4,3,2) – замкнутый путь.

Для событий рассчитывают 3 характеристики: ранний и поздний срок совершения события, а также его резерв.

Ранний срок совершения события определяется величиной наиболее длительного отрезка пути от исходного до рассматриваемого, причем t_p(1)=0, a t_p(N)=t_кр.

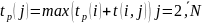
Рассмотрим на примере

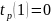
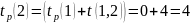
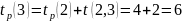
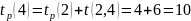
К вершине 5 можно прийти 2-мя путями:

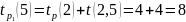
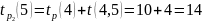
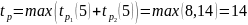
Таким образом, для события 5 ранний срок завершения работы равен 14.

Вычислим остальные:

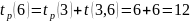
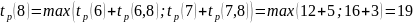
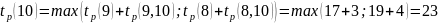
Поздний срок совершения событий характеризует самый последний допустимый срок, которому должно совершиться событие, не вызывая при этом срыва срока совершения последнего события.

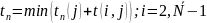
Этот показатель определяется «обратным ходом», с учетом соотношения

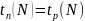
Все события, за исключением событий, принадлежащих критическому пути, имеют резерв

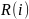
Пример №14

Вычислить .

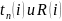Резерв показывает, на какой предельно допустимый срок можно задержать наступление этого события, не вызывая при этом срыва срока выполнения всего комплекса работ.

Путь характеризуется двумя показателями – продолжительностью и резервом, резерв пути определяется как разность между длинами критического и рассматриваемого путей.