Пример №3

Две организации выпускают изделия трех видов (А, В и С) первой, второй и третьей категории качества

Категория качества	Число изделий, выпущенных
	Первой организации			Второй организации
	Изделие А	Изделие В	Изделие С	Изделие А	Изделие В	Изделие С
Высшая	500	300	600	600	800	1100
Первая	240	160	200	200	280	360
Вторая	30	24	36	50	40	60

Число изделий, произведенных первой организацией, можно отобразить в виде матрицы А, а второй организацией – виде матрицы В.

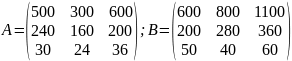
Обе матрицы одного типа – (3,3). Чтобы определить общее число изделий каждого вида и каждой категории качества, выпущенных двумя организациями, надо произвести сложение матриц.

Допустим, что вторая организация не смогла выпустить изделия вида С. В этом случае матрицы А(3,3) и В(3,2) не являются однотипными и их сложение производить нельзя. Чтобы матрица В имела тот же тип, что и матрица А, необходимо добавить фиктивный столбец с нулевыми элементами:

Пример №3

Вычислить произведение матриц

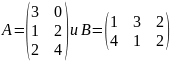
Анализ матриц А(3,2) и В(2,3) показывает, что они соответствуют друг другу, следовательно, процесс умножения матриц возможен.

Вычислим значения каждого элемента матрицы С как произведение i-й строки матрицы А и k-го столбца матрицы В: с₁₁=3·1+0·4=3; с₁₂=3·3+0·1=9; ….; с₃₂=2·3+4·1=10: с₂₃=2·2+4·2=12.

Таким образом, произведение матриц будет иметь вид

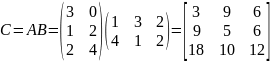
7. Модели сетевого планирования и управления

7.1. Основные понятия сетевой модели

Сетевой моделью (сетевым графиком) называется экономико-математическая модель, отражающая комплекс работ и событий, связанных с реализацией некоторого проекта, в их логической и технологической последовательности и связи.

Методы сетевого моделирования относятся к методам принятия оптимальных решений.

Анализ сетевой модели позволяет:

• Более четко выявить взаимосвязи этапов реализации проекта

• Определить наиболее оптимальный порядок выполнения этих этапов

Математический аппарат сетевых моделей базируется на теории графов.

Графом называется совокупность двух конечных множеств: вершин и ребер.

Рис. – График двух конечных множеств

Вершины – это пронумерованные точки, отрезки, соединяющие пару вершин называются ребрами.

Если на каждом ребре задается направление (пары вершин являются упорядоченными), то граф называется ориентированным.

В противном случае он называется не ориентируемым.

Последовательность повторяющихся ребер, ведущая от некоторой вершины к другой образует путь.

Граф называется связным, если для любых двух его вершин существует путь, их соединяющий; в противном случае граф называется несвязным.

Сетевая модель представляет собой граф в виде «сеть».

Сеть – это ориентированный конечный связный граф, имеющий начальную величину (источник) и каноническую вершину (сток).