Пример №1
Описать в виде матрицы инцидентности неориентированный граф
|
1 |
2 |
3 |
4 |
5 |
6 |
1 |
|
1 |
0 |
0 |
0 |
0 |
2 |
1 |
|
1 |
0 |
1 |
0 |
3 |
0 |
1 |
|
1 |
0 |
0 |
4 |
0 |
0 |
1 |
|
1 |
1 |
5 |
0 |
1 |
0 |
1 |
|
0 |
6 |
0 |
0 |
0 |
1 |
0 |
|
Решение задачи начинается с построения сетки размером (6 на 6), т.е. по числу вершин графа. Первая строка соответствует первой вершине графа, которая связана только с вершиной 2 (т.е. а12=1, а остальные элементы строки равны нулю). Вторая вершина имеет связи с вершинами 1, 3 ,5, поэтому а21=а23=а25=1, остальные элементы второй строки нулевые. Аналогично заполняются другие строки матрицы.
В матрице инцидентности единица означает только наличие связи между двумя вершинами графа. Однако такая матрица позволяет отобразить и интенсивность связи. На рисунке показан фрагмент сети автомобильных дорог с указанием протяженности участков. Ему соответствует матрица инцидентности, в которой элементы aij соответствуют длине участков дороги.
0 |
10 |
15 |
0 |
0 |
10 |
0 |
0 |
8 |
0 |
15 |
0 |
0 |
9 |
0 |
0 |
8 |
9 |
0 |
30 |
0 |
0 |
0 |
30 |
0 |
Поскольку граф неориентированный, матрица является симметричной. В ней наличие связи отображается не единицей в ненулевой клетке, а цифрой, соответствующей длине участка дороги.
Две матрицы А=(aij)(m,n) и В= (bik)(p,q) считаются равными, если выполняются два условия:
1. Совпадает тип матрицы, т.е. m=p, n=q;
2. Все соответствующие элементы матриц равны, т.е. aik=bik.
Пример №2.
Имеются шесть специализированных подразделений, которые необходимо объединить в комплексную структуру. Признаками объединения (кластеризации) являются технологическая зависимость (aт.з.ik) и территориальная близость (aт.б.ik) подразделений.
Технологическая зависимость отображена на рисунке. Графу технологической зависимости соответствует матрица инцидентности Ат.з.
|
Ат.з=
|
Территориальную близость (удаление подразделений друг от друга в процессе работ) отображает матрица Бт.б. (расстояния указаны в километрах):
Бт.б.=
Элементы матрицы Бт.б. имеют размерность в километрах, для удобства расчетов эту матрицу следует привести к нормированному виду, представив aт.з.ik в долях единицы. Для этого все значения aт.з.ik надо разделить на максимальное значение удаленности подразделений ат.б.16=ат.б.26=ат.б.61=ат.б.62=10 км. В результате образуется нормированная матрица
Бн.т.б.=
Поскольку в один кластер надо объединять подразделения, технологически зависимые и расположенные вблизи друг от друга, необходимо сформировать обобщенный показатель близости подразделений аΣik=aт.з.ik+aт.б.ik, т.е. провести сложение матриц.
Суммой матриц А и В называется матрица С, в которой каждый элемент cik есть сумма элементов aik и bik .
В рассматриваемом примере матрица С=Ат.з+Бнт.б. имеет следующий вид:
С=
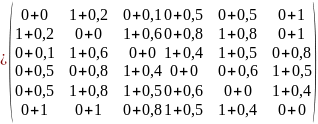
Суммарная матрица отображает силу связи подразделений по обобщенному критерию. Например, наиболее связными являются элементы 5 и 2 (а52=а25=1,8). Следовательно, эти подразделения надо в первую очередь объединять в общую структуру. Следующими сильно связными подразделениями являются подразделения 3 и 2 (а23=а32=1,6). Аналогичным образом определяют и другие связные подразделения. Порядок формирования организационной структуры по такому алгоритму рассматривается далее на подробном примере.
При сложении матриц используются следующие правила:
Суммарные матрицы должны быть одного типа
Матрицы разного типа можно привести к однотипным, если в одну из них добавить фиктивную строку или столбец с нулевыми элементами.
Каждый элемент матрицы суммы С (сik) получается сложением элементов суммируемых матриц А (аik) и В (bik) с одинаковыми индексами, т.е.
(аik)(m,n) + (bik)(m,n) =(сik)(m,n)