Пример №11

Продолжительность каждой из работ является случайной величиной со среднеквадратическим отклонением, определяется по формуле

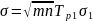
где m - число захваток; n – число машин в частном потоке (в специализированном подразделении), если в потоке имеется несколько типов машин (как, например, при укладке асфальтобетонной смеси) в расчет принимается ведущая машина (асфальтоукладчик); 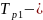время выполнения работы на каждой из захваток строящейся дороги;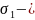 среднеквадратическое отклонение производительности отдельно взятой машины.

Рассчитать среднеквадратическое отклонение времени завершения земляных работ по графику. Число захваток m=10, время обработки каждой из них 1 смена, число ведущих мащин (бульдозеров) n=5, 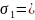0,26.

Подставив значения в формулу, получим

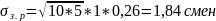
5.2. Статистический контроль качества

Понятие надежности отождествляется с понятием качества. Высокое качество конструкций, материалов, производства работ создает гарантию надежности (если сооружение будет правильно эксплуатироваться). Поэтому в строительстве контролю качества уделяет первостепенное внимание.

Следует различать два вида контроля качества:

1) статистическое регулирование качества, основанное на ведении контрольных карт

2) текущий контроль производственного процесса методами математической статистики (математико-статистические выборочные методы), применяемый при приеме готовых изделий.

Статистическое регулирование качества продукции.

Статистическое регулирование качества - это текущий контроль производственного процесса в целях предупреждения брака. Такое регулирование осуществляется при производстве строительных конструкций, строительных материалов на предприятиях производственной базы. Если контролируемые параметры начинают выходить за пределы установленных границ или становятся близкими к ним, осуществляется вмешательство в технологический процесс.

Статистические методы выборочного контроля.

Данная группа статистических методов применяется для осуществления входного, промежуточного и окончательного контроля готовой продукции на предмет ее соответствия техническим требованиям или требованиям к качеству, согласованным заказчиком и изготовителем (поставщиком). Эти методы прямого воздействия на производство не отказывают, но косвенно влияют на него, выявляя брак готовой продукции.

Контроль все выпускаемой продукции предприятия невозможен либо по экономическим соображениям, либо из - за необходимости разрушения конструкции при контроле ее прочность на характеристик. Поэтому на практике применяют выборочный контроль, заключающийся в проверке выборок из партии продукции. Результаты проверки позволяют сделать заключение о качестве продукции.

Пример №12

При проверке качества изготовления звеньев железобетонных труб диаметром 1м в качестве контролируемого признака выбран внутренний диаметр кольца трубы (звена). Установлены контрольные границы К_в=101см, К_н=99 см (а=100 см). в смену изготавливается 1000колец, из которых выборочному контролю подлежат 30. Партия считается годной, если доля брака не превышает 10%.

Рассчитаем основные параметры диаграммы

По условию а=100 см, N=1000 ед., n=30 ед., С=30·0,1=3 ед.

Как видно на рисунке

Рис. 3 Предельная диаграмма одновыборочного плана контроля

Первые 3 кольца оказались качественными, а 4 кольцо - бракованным. В точке, соответствующей 3 кольцу, траектория брака поднялась на один уровень (b=1). Последующие выбранные кольца оказались годными, а 28-е – бракованным. На этом номере траектория брака поднялась еще на один уровень (b=2). Поскольку два последних кольца (29-е и 30-е) оказались годными, траектория нарастания брака пересекла вертикальную линию в точке, соответствующей значению b=2, т.е. ниже предельной точки С=3. Таким образом, партия из 100 колец может быть принята.

П рактика контроля качества показала, что рассмотренный одновыборочный контроль не всегда удовлетворяет производителя продукции либо ее потребителя. В таких случаях применяют двухвыборочный контроль, при котором вместо двух параметров (n и С) и однократной выборки используют пять (или четыре) параметра (n₁, n₂,C₁, C₂, C₃) и двукратную выборку.

Рис.4

Если в первой выборке объемом n₁ содержится максимум C₁ негодных изделий (т.е. выполняется уровень b₁ C₁), то партия принимается (рис).

Если b₁>C₂(C₂>C₁), партия бракуется. Здесь параметр С₂ играет роль второго допустимого предела нормы брака (например, при жесткой норме допускается 5% брака; эту норму можно немного смягчить, приняв в качестве допустимого значения 10%).

Если С₁<b₁<C₂, делается вторая выборка объемом n₂ деталей (изделий), в которой может содержаться b₂ негодных деталей. При b=b₁+b₂ партия принимается, если выполняется условие b≤C₃ (C₃>C₂). В противном случае (т.е. при b>C₃) партия бракуется.

В отличие от одновыборочного контроля здесь в первой выборке n₁ имеются три предельные зоны: «принятие», «браковка», «продолжение контроля», разделенные числами С₁ и С₂. Во второй выборке выделяются две зоны: «принятие» и «браковка». На второй предельной линии n₁+n₂ эти зоны разделяет точка, соответствующая числу С₃. Решение принимают в зависимости от того, где заканчивается траектория нарастания брака во второй выборке.

Одновыборочный контроль качества эффективен для партии с очень высоким или очень низким процентом брака. Здесь решения очевидны: в первом случае партия бракуется, во втором – принимается.

Двухвыборочный контроль предпочтительнее, когда продукция имеет среднее качество и решение, принятое на основе одной выборки, неоднозначно, требуется дополнительная информация о годности продукции.