1.2. Характеристики поля излучения

10. Поток частиц (фотонов) F(t) – отношение числа частиц (фотонов) dN, пересекающих заданную поверхность за интервал времени dt, к величине этого интервала:

F = . (1.14)

Размерность – 1/с.

11. Флюенс частиц (фотонов) Ф – отношение числа частиц (фотонов) dN, проникающих в элементарную сферу, к площади поперечного сечения этой сферы dS:

Ф = . (1.15)

Размерность  1/м²; 1/см².

12. Плотность потока частиц³ (фотонов)  – отношение изменения флюенса частиц (фотонов) dФ за интервал времени dt, к величине этого временного интервала:

 = . (1.16)

Размерность  1/(см²₎; 1/(ссм²_).

Для точечного изотропного источника с активностью А(t) и выходом частиц  плотность потока частиц (t,r) в вакууме в любой момент времени t и в любой точке на расстоянии r от источника равна

(t, r) = . (1.17)

При известной временной зависимости плотности потока частиц (t) флюенс Ф за временной интервал t = t₂ – t₁ получается интегрированием

. (1.18)

13. Поток энергии F_ – отношение изменения энергии излучения d частиц и фотонов, пересекающих заданную поверхность за интервал времени dt, к величине этого интервала:

F_ . (1.19)

Размерность потока энергии – Вт, Дж/с, МэВ/с.

14. Флюенс энергии  отношение энергии излучения d, падающей на сферу с площадью поперечного сечения dS, к площади этого сечения:

= . (1.20)

Размерность – Дж/м², МэВ/см².

15. Плотность потока энергии (или интенсивность излучения I) – отношение изменения флюенса энергии d за интервал времени dt к величине этого интервала:

I = = . (1.21)

Размерность – Вт/м², Дж/(м²с), МэВ/(cм²с).

Для моноэнергетического излучения с энергией  интенсивность излучения I связана с плотностью потока частиц (фотонов)  соотношением

. (1.22)

Если излучение немоноэнергетическое, то необходимо знать спектр (энергетическое распределение) d/d, тогда интенсивность получается интегрированием по спектру:

. (1.23)

ЗАДАЧИ

1.1. Какова активность (без учета дочерних продуктов) а) 1 г и б) 1 г ? Во сколько раз активность больше активности ?

1.2. Определить период полураспада и постоянную распада  радионуклида, если за сутки его активность уменьшилась на а) 75 %; б) 0,01 %.

1.3. Определить массу 1 Ки естественного урана без учета дочерних продуктов (весовой состав приведен в табл. П.5).

1.4. Определить массу активных атомов нуклида ²³⁹Pu активностью а) 10 Бк, б) 10 Ки.

1.5. Определить в процентах (по массе) состав радиоактивных атомов ⁵⁹Fe в образце металлического железа активностью 10¹⁰ Бк и массой 10 г.

1.6. Определить удельную активность ⁴⁰К в образце, представляющем собой соль KCl, если содержание ⁴⁰К в естественном калии составляет 0,0118 % по массе.

1.7. Какой активностью обладает вагон с калийными удобрениями (KNO₃), если масса удобрений 50 т, а содержание ⁴⁰К в естественном калии составляет 0,0118 % по массе?

1.8. В известняковых почвах удельная активность ²³⁸U составляет 30 Бк/кг. Сколько миллиграммов ²³⁸U содержит 1 кг известняка?

1.9. Определить, сколько свинца ²⁰⁶Pb образовалось из 1 кг ²³⁸U за время существования Земли (4,510⁹ лет).

1.10. Определить возраст древнего деревянного корабля, если известно, что активность изотопа ¹⁴С, содержащегося в нем, составляет 90 % активности того же изотопа в только что срубленных деревьях.

1.11. Источник ⁴⁰К имеет активность 10⁴ Бк. Найти число атомов ⁴⁰К, содержащихся в этом источнике.

1.12. Точечный изотропный радиоактивный источник , схема распада которого приведена на рис. 1.2, испускает 510⁷ фотон/с. Рассчитать активность источника с учетом аннигиляционного излучения, предполагая, что все испускаемые позитроны поглощаются в источнике.

1.13. Рассчитать квантовые выходы всех -квантов, испускаемых радионуклидом, схема распада которого изображена на рис. 1.3. Относительные выходы -квантов с разной энергией относятся как ₁(0,5 МэВ):₂(2 МэВ):₃(2,75 МэВ) = 18:5:7;

₄(1,5 МэВ):₅(2,25 МэВ) = 14:5.

2,52 ч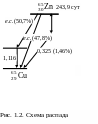

1.14. Нарисовать схему распада , если испускаются только -кванты с энергией 0,835 МэВ и квантовым выходом 100 %.

1.15. Нарисовать схему распада радионуклида, если испускаются следующие -кванты и -частицы:

= 0,3 МэВ, = 20 %; = 0,5 МэВ, = 30 %; = 1,0 МэВ, = 50 %; = 0,2 МэВ, = 10 %; = 0,7 МэВ, = 10 %; = 0,5 МэВ, = 40 %; = 1,1 МэВ, = 100 %.

1.16. Нарисовать схему распада радионуклида, если в паспорте на источник указано, что он – чистый излучатель аннигиляционных фотонов с внешним выходом а) 200 %, б) 150 %.

1.17. При радиоактивном распаде ядер изотопа А₁ с постоянной распада ₁ образуется изотоп А₂ с постоянной распада ₂. Получить закон изменения числа радиоактивных ядер изотопа А₂ с течением времени, полагая, что в начальный момент препарат содержал только ядра А₁ в количестве N₁₀.

1.18. При радиоактивном распаде ядер нуклида А₁ с периодом полураспада 10 ч образуется нуклид А₂ с периодом полураспада 15 ч. Предполагая, что в начальный момент образец содержал только ядра А₁, определить, через какой промежуток времени количество ядер А₂ достигнет максимума.

1.19. Образец ²²⁶Ra был запаян в ампулу. Через сутки была измерена активность радона ²²²Rn (Т_1/2 = 3,823 сут), которая составила 510⁶ Бк. Определить активность ²²⁶Ra, которой он обладал перед запайкой ампулы.

1.20. Плотность потока фотонов, создаваемых источником ⁵⁸Со, в начальный момент времени в точке детектирования составляла 10⁸ фотон/(см²с). Определить флюенс фотонного излучения в точке детектирования за время облучения 13 ч.

1.21. В первом сосуде объемом 60 л находится радиоактивная жидкость, имеющая объемную активность 2,310² Бк/м³, во втором сосуде объемом 90 л объемная активность составляет 1,610³ Бк/м³. Жидкости из сосудов перелили в общий сосуд и разбавили 100 л дистиллята. Найти объемную активность среды в общем сосуде.

1.22. Какова будет объемная активность воздуха, если зал объемом 10³ м³ с объемной активностью воздуха 12 Бк/л сообщить с помещением объемом 500 м³ с объемной активностью воздуха 5 Бк/л?

1.23. Рассчитать плотность потока -квантов на расстоянии 1 м от точечного изотропного источника ⁶⁰Со активностью 10¹⁰ Бк.

1.24. Вычислить количество радиоактивных ядер в образце, содержащем ⁹⁰Y, если при измерении на установке с эффективностью счета⁴ 8 % скорость счета -частиц составляет 10⁵ част./мин.

1.25. Определить кинетические энергии электрона и позитрона, образующихся в элементарном акте эффекта образования пар в поле ядра, если энергия фотона равна 10 МэВ, а кинетическая энергия при образовании пары распределяется практически поровну между электроном и позитроном. Какая энергия будет поглощена в детекторе, если аннигиляционные -кванты покинут его объем? Тормозное излучение электронов и позитронов не учитывать.

1.26. Определить активность точечного изотропного источника ¹³⁷Cs, находящегося на расстоянии 30 см от дискового детектора ( 6 см), если поток -квантов, падающих на поверхность детектора, составляет 10³ 1/с. Поверхность детектора расположена перпендикулярно линии, соединяющей центры источника и диска.

1.27. Флюенс фотонов от точечного изотропного источника ⁵⁹Fe в точке детектирования составил 10¹² 1/см². Найти начальную активность источника, если облучение длилось три месяца, а расстояние от источника до детектора равнялось 10 см.

1.28. Точечный изотропный источник ⁵¹Cr в начальный момент имеет активность 10⁸ Бк. Найти флюенс фотонного излучения за год на расстоянии 50 см от источника.