43

2.2. Дифференциал

Рассмотрим приращение функции в точке :

.

Мы будем говорить, что функция y имеет дифференциал (дифференцируема) в точке х=а, если приращение можно представить в виде:

, (1)

где А = const, a (x) - бесконечно малая величина более высокого порядка, чем х, т.е. . (2)

Определение. Дифференциалом функции y=f(x) в точке х=а называют главную часть приращения функции в этой точке, линейно зависящую от приращения аргумента.

Обозначают дифференциал одним из следующих символов: dy, df.

Таким образом, по определению

(3)

в силу формулы ( 1 ).

Теорема. Функция имеет в точке дифференциал тогда и только тогда , когда она имеет производную в этой точке, при этом в формуле (3) , .

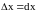Доказательство. Пусть функция y=f(x) имеет дифференциал в точке х=а. Тогда из (1) следует, что

, (4)

где - бесконечно малая величина в силу (2).

Согласно основной теореме теории пределов имеет предел при , равный А. Это означает, что функция y имеет производную в точке а и при этом . Следовательно,

. (3)

Формула (3^’) справедлива для любых функций. В частности, для y=x получаем , т.е. . Тогда

. (5)

Обратно, пусть функция y = f(x) имеет при х = а производную.

По определению .

В силу основной теоремы теории пределов это означает, что

,

где - бесконечно малая величина при .

Отсюда , где . Ясно, что последнее равенство представляет собой соотношение (1), в котором .

Что и требовалось доказать.

Следствие 1. Дифференциал независимой переменной совпадает с ее приращением.

Следствие 2. Производная функции есть отношение дифференциалов зависимой и независимой переменных . (Ранее мы использовали как обозначение).

2.2.1. Геометрический смысл дифференциала

В предыдущей теореме было показано, что dy = y'x.

Найдем приращение касательной (y)_k в точке х = а. Уравнение касательной имеет вид:

y = y (a) + y' (a)  (x - a).

Ясно, что y (a + x) = y (a) + y' (a)  (a + x - a) = y (a) + y' (a) x.

Следовательно,

(y)_k = y (a + x) - y (a) = y (a) + y' (a) x - y (a) = y' (a) x.

Таким образом, приращение ординаты касательной есть дифференциал функции в рассматриваемой точке.

2.2.2. Инвариантность формы дифференциала

Под инвариантностью дифференциала понимают неизменность формулы (5) для вычисления дифференциала независимо от того, является ли аргумент конечным или промежуточным.

Итак, мы показали, что

dy = ydx. (5)

Вычислим dy, предполагая, что у - сложная функция, т.е. y = y(u), u = u(x).

По формуле для дифференцирования сложной функции ,

поэтому в силу (5) имеем:

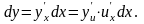
Но поэтому .

Последняя формула отличается от (5) лишь обозначением аргумента, несмотря на то, что он является промежуточным.

Следовательно, дифференциал обладает свойством инвариантности.