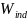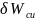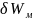- •1 Моделирование процесса измерения белизны
- •Спецификация измеряемой величины
- •Идентификация объекта измерений
- •1.3 Принцип и метод измерений
- •1.4 Функциональный анализ методики выполнения измерений
- •2 Обработка результатов прямых многократных измерений на базе теории погрешностей
- •3 Оценка показателей точности результатов измерений
- •3.1 Оценка точности результатов внутрилабораторных измерений
- •3.2 Оценка точности результатов межлабораторного эксперимента
- •4 Разработка методики оценивания неопределенности измерения белизны
- •Библиография
4 Разработка методики оценивания неопределенности измерения белизны
4.1. Измерительная задача
Для измерения уровня белизны используют фотометр белизны и цветовых характеристик «КОЛИР» (далее по тексту – фотометр). В основе работы фотометра лежит спектрофотометрический метод измерений спектральных коэффициентов диффузного отражения контролируемого материала и расчета его белизны и цветовых характеристик. Световой поток от лампы, рассеянный внутренней поверхностью интегрирующего шара, освещает контролируемый образец диффузным светом. Отраженный от контролируемого образца световой поток, в который последовательно вводятся светофильтры (с числом выборки 18 в спектральном диапазоне 400 до 740 нм), попадает в фотоприемное устройство, где преобразуется в электрические сигналы, пропорциональные измеренным значениям. Сигналы усиливаются до необходимого уровня и передаются в устройство управления, где происходит их обработка. Результаты измерений индуцируются на индикаторе.
Вид измерения: прямое, однократное. Основные метрологические характеристики:
Диапазон измерений координат цветности (x,y) для источника света А,С, Д65 по ГОСТ 7721, условные единицы:
-x- от 0,004 до 0,734;
-y- от 0,005 до 0,834
Пределы допускаемой абсолютной погрешности при измерении координат цветности ± 0,02.
Диапазон измерений белизны материалов, не содержащих оптические люминесцентные отбеливатели – от 20 до 100 %.
Пределы допускаемой абсолютной погрешности при измерении белизны материалов, не содержащих оптические люминесцентные отбеливатели - ± 0,5 %.
Пределы допускаемого абсолютного отклонения при индикации белизны материалов, содержащих оптические люминесцентные отбеливатели - ± 1,0%.
Фотометр изображен на рис. 4.1
|
|
Рисунок 4.1 – Фотометр белизны и цветовых характеристик «КОЛИР»
4.2. Математическая модель и данные
Результаты измерений белизны:
W = 95,8 %; 88,1 %; 79,4 %; 80,7 %; 90 %; 97,2 %; 84,3 %; 78,9 %; 98,4 %; 90,1%
Среднее значение белизны из 5 наблюдений:
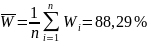
Составляем математическую модель измерения.
W = Wind + WСИ + WМ + WОП + WУСЛ,
где Wind – точечная оценка измеряемой величины, %;
WСИ – поправка на основную погрешность фотометра, %;
WМ – поправка, обусловленная несовершенством метода измерений, %;
WОП – поправка, обусловленная индивидуальными особенностями оператора, %;
WУСЛ – поправка на погрешность фотометра от изменения условий от нормальных, %.
Суммарная стандартная неопределённость:
uс(С)
=
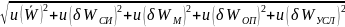
Анализ источников изменчивости
Таблица 4.1
-
Источник изменчивости
Факторы
Экспертная оценка
W
Wси
Учитывается
Wмет
Учитывается
Wоп
Учитывается
Wусл
Не учитывается
Wси
Wф - поправка на основную погрешность фотометра
Учитывается
Wк - поправка на калибровку фотометра
Не учитывается
Wм
Wвыч - поправка на вычисление
Не учитывается
Wокр - поправка на округление
Учитывается
-
Wоп
Wинт - поправка на интерполирование
Не учитывается
Wман - поправка на манипулирование
Не учитывается вследствие того, что оператор обладает достаточной квалификацией
Wсч - поправка на считывание
Не учитывается
Wусл
Wвл - поправка на изменение влажности
Не учитывается
Wд - поправка на изменение давления
Не учитывается
Wт - поправка на изменение температуры
Не учитывается
4.3. Анализ источников изменчивости
Диаграмма причинно-следственной связи с источником изменчивости для белизны:


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4.4 Построение окончательной модели измерений белизны
W = Wind + Wси+ Wм
4.5. Анализ входных величин и их неопределённостей
Таблица 4.2 – Анализ входных величин при оценивании неопределенности измерения белизны:
Входная величина: Белизна, W, %
|
Тип оценивания неопределенности: А Вид распределения: нормальное Значение
оценки:
Стандартная неопределенность: 2,39 % |
З
начение
величины определялось из многократных
наблюдений по показывающему устройству
– фотометру белизны и цветовых
характеристик «КОЛИР». Значение
точечной оценки получили по формуле
|
|
Входная величина: Поправка, обусловленная техническим несовершенством средства измерения, Wси % |
Тип оценивания неопределенности: B Вид распределения: равномерное Значение оценки: 0,5% Стандартная
неопределенность: 0,29
|
Допустимое
отклонение для цифрового фотометра
по паспортным данным составляет
|
|
Входная величина: Поправка, обусловленная несовершенством метода, Wм % |
Тип оценивания неопределенности: B Вид распределения: равномерное Значение оценки: 0,01 % Стандартная неопределенность: 0,0057 % |
Значение величины определялось из паспорта, согласно которому номинальная ступень квантования равна 0,01%. Полагая, что величина распределена равномерно, определяем стандартное отклонение для равномерного распределения: u(Wм) = 0,01/ ≈ 0,0057 %. |
|
4.6. Оценка ковариации
Ковариация, связанная с оценками входных величин, в нашем случае равна нулю, т.к входные величины являются независимыми друг от друга, поэтому пренебрежем ковариацией.
4.7. Расчёт оценки выходной величины
Точечную оценку прямых многократных измерений определяем как их среднее арифметическое:
4.8. Бюджет неопределённости.
Составляем бюджетную неопределённость измерения белизны:
Таблица 4.3 – Бюджет неопределённости измерения белизны
Величина Xi |
Единица измерения |
Оценка xi
|
Тип оценивания неопределенности |
Распределение вероятностей |
Стандартная неопределенность u (xi) |
Вклад в неопределенность ui(W), % |
|
% |
85,8 |
А |
нормальное |
2,32 |
98,26 |
|
% |
0,5 |
В |
равномерное |
0,29 |
1,57 |
|
% |
0,01 |
В |
равномерное |
0,0057 |
0,0006 |
4.9. Расчёт суммарной стандартной неопределённости
uс
(W)
=
 =
=
=
=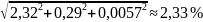 .
.
Сравним вклады источников неопределенности в суммарную стандартную неопределенность. Процентный вклад неопределенности, белизны:
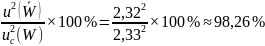
Процентный вклад неопределённости поправки, обусловленной погрешностью фотометра ΔWСи:

Процентный вклад неопределённости поправки, обусловленной погрешностью метода ΔWм:
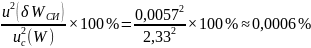
4.10. Расчёт расширенной неопределённости
Для уровня доверия p = 0,95 (коэффициент охвата k = 2):
Uр (W) = 2 · 2,33 = 4,66 %.
Для уровня доверия p = 0,99 (коэффициент охвата k = 3):
Uр (W) = 3 · 2,33 = 6,99 %.
4.11. Результат измерения:
Белизна составляет (88,29 4,66) %, где число, следующее за знаком «», является численным значением расширенной неопределенности, которая получена умножением суммарной стандартной неопределенности на коэффициент охвата k = 2, основанный на предполагаемом нормальном распределении, и определяет интервал, соответствующий вероятности охвата приблизительно 95 %.
Белизна составляет (88,29 6,99) %, где число, следующее за знаком «», является численным значением расширенной неопределенности, которая получена умножением суммарной стандартной неопределенности на коэффициент охвата k = 3, основанный на предполагаемом нормальном распределении, и определяет интервал, соответствующий вероятности охвата приблизительно 99 %.

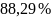
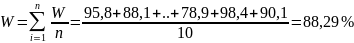 ,
где Wi
– i-й
результат наблюдения, n
– число результатов наблюдений.
Стандартная неопределенность получена
из СКО среднего значения величины и
равна
,
где Wi
– i-й
результат наблюдения, n
– число результатов наблюдений.
Стандартная неопределенность получена
из СКО среднего значения величины и
равна
 =
u(W) /
=
u(W) /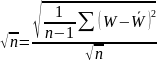 = 2,32
%
.
= 2,32
%
.
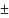 0,5
%, стандартная неопределенность
определялась как u(δWф)
= 0,5/
0,5
%, стандартная неопределенность
определялась как u(δWф)
= 0,5/ ≈ 0,29 %.
≈ 0,29 %.