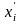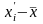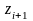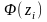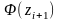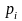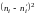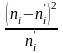- •1 Моделирование процесса измерения белизны
- •Спецификация измеряемой величины
- •Идентификация объекта измерений
- •1.3 Принцип и метод измерений
- •1.4 Функциональный анализ методики выполнения измерений
- •2 Обработка результатов прямых многократных измерений на базе теории погрешностей
- •3 Оценка показателей точности результатов измерений
- •3.1 Оценка точности результатов внутрилабораторных измерений
- •3.2 Оценка точности результатов межлабораторного эксперимента
- •4 Разработка методики оценивания неопределенности измерения белизны
- •Библиография
2 Обработка результатов прямых многократных измерений на базе теории погрешностей
Согласно заданию на курсовую работу задан массив результатов измерений одной и той же физической величины (таблица 2.1).
Таблица 2.1- Исходные данные (читать построчно):
0,002 |
0,001 |
0,001 |
-0,006 |
-0,005 |
-0,017 |
0,014 |
-0,027 |
0,017 |
0,033 |
0,004 |
-0,003 |
0,013 |
0,000 |
0,010 |
0,010 |
0,009 |
0,000 |
0,013 |
0,010 |
0,002 |
-0,016 |
-0,006 |
0,018 |
0,011 |
0,014 |
0,004 |
0,014 |
0,014 |
0,005 |
-0,014 |
0,017 |
0,014 |
0,011 |
-0,015 |
0,004 |
0,005 |
0,033 |
-0,021 |
-0,003 |
0,019 |
0,009 |
-0,004 |
0,002 |
0,021 |
0,016 |
-0,012 |
0,001 |
0,025 |
0,012 |
0,021 |
0,020 |
-0,011 |
0,009 |
0,010 |
0,011 |
0,011 |
0,039 |
0,016 |
-0,006 |
0,032 |
-0,110 |
0,033 |
В качестве первичной оценки погрешности измерений в серии, включающей систематическую и случайную составляющие, может быть использован размах результатов многократных измерений:
R′ = Xmax – Xmin = 0,039- ( -0,110)=0,149.
По заданным результатам измерений строим с помощью пакета STATISTICA точечную диаграмму результатов измерений в выбранном масштабе. Результат построения диаграммы показан на рисунке 2.1:

Рисунок 2.1 - Точечная диаграмма
На основе точечной диаграммы заключаем, что в результатах измерений присутствуют прогрессирующие систематические погрешности. Обнаружены результаты с грубой погрешностью (-0,110). Статическую обработку результатов проведем без них (таблица 2.2) и результат построения диаграммы представлен на рисунке 2.2.
Таблица 2.2 – Исправленные результаты измерений (читать построчно):
0,002 |
0,001 |
0,001 |
-0,006 |
-0,005 |
-0,017 |
0,014 |
-0,027 |
0,011 |
0,033 |
0,004 |
-0,003 |
0,013 |
0,000 |
0,010 |
0,010 |
0,009 |
0,000 |
0,013 |
0,010 |
0,002 |
-0,016 |
-0,006 |
0,018 |
0,011 |
0,014 |
0,004 |
0,014 |
0,014 |
0,005 |
-0,014 |
0,017 |
0,014 |
0,011 |
-0,015 |
0,004 |
0,005 |
0,033 |
-0,021 |
-0,003 |
0,019 |
0,009 |
-0,004 |
0,002 |
0,021 |
0,016 |
-0,012 |
0,001 |
0,025 |
0,012 |
0,021 |
0,020 |
-0,011 |
0,009 |
0,010 |
0,011 |
0,011 |
0,039 |
0,016 |
-0,006 |
0,032 |
0,033 |
|

Рисунок 2.2 – Точечная диаграмма
Расчёт отклонений Vi.
Аппроксимируем точечную диаграмму кривой, как показано на рисунке 2.3:

Рисунок 2.3 - Аппроксимация результатов измерений
Уравнение аппроксимирующей прямой имеет следующий вид:
y = -0,0004+0,0002*х
где x – номер точки, y – величина измеренной величины
Проведём статистическую обработку данных. Для этого исключим систематические составляющие в данной диаграмме. Обозначим на рисунке 2 эквидистанты. Из полученной диаграммы исключим грубые погрешности (рисунок 2.4):



R
R’ЭЭ
Рисунок 2.4 – Точечная диаграмма
При «частичном исправлении» результатов наблюдений с использованием точечных диаграмм под Xср понимают «текущее среднее значение», определяемое по аппроксимирующей линии. В таком случае за отклонение Vi принимают отклонение каждого из наблюдений от аппроксимирующей линии в масштабе точечной диаграммы.
Подсчитаем отклонения по формуле: Vi = Xi -Xср и представим результаты в таблице 2.3.
Таблица 2.3 – Значения отклонений от аппроксимирующей линии (читать построчно)
0,0022 |
0,001 |
0,0008 |
-0,0064 |
-0,0056 |
-0,0178 |
0,013 |
-0,0282 |
0,0156 |
0,0314 |
0,0022 |
-0,005 |
0,0108 |
-0,0024 |
0,0074 |
0,0072 |
0,006 |
0,0032 |
0,0096 |
0,0064 |
-0,0018 |
-0,02 |
-0,0102 |
0,0136 |
0,0064 |
0,0092 |
-0,001 |
0,0088 |
0,0086 |
-0,0006 |
-0,0198 |
0,0011 |
0,0078 |
0,0046 |
-0,0216 |
-0,0028 |
-0,002 |
0,0258 |
-0,0284 |
-0,0106 |
0,0112 |
0,001 |
-0,00122 |
-0,0064 |
0,0124 |
0,0072 |
-0,021 |
-0,0082 |
0,0156 |
0,0024 |
0,0112 |
0,01 |
-0,0212 |
-0,0014 |
-0,0006 |
0,0002 |
0 |
0,0278 |
0,0046 |
-0,0176 |
0,0202 |
0,021 |
|
|
|
Правильность расчётов значений отклонений можно проверить с помощью формулы:
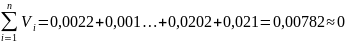
Расчет оценки СКО результатов наблюдений по формуле:
Рассчитаем оценку среднего квадратического отклонения результатов наблюдений
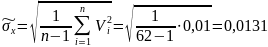
Строим гистограмму распределения частот по отклонениям от аппроксимирующей линии (рисунок 2.5):

Рисунок 2.5 – Гистограмма распределения
При проверке гипотезы о нормальном распределения случайной величины Х с помощью критерия - Пирсона составляем следующую таблицу 2.4:
Таблица 2.4
№ |
|
|
|
|
|
|
|
|
1 |
-0,027 |
-0,0175 |
- |
-0,0250 |
0 |
-1,906 |
-0,5 |
-0,4713 |
2 |
-0,0175 |
-0,0081 |
-0,0250 |
-0,0156 |
-1,906 |
-1,190 |
-0,4712 |
-0,3830 |
3 |
-0,0081 |
0,00128 |
-0,0156 |
-0,0062 |
-1,1901 |
-0,4737 |
-0,3830 |
0,1808 |
4 |
0,00128 |
0,01071 |
-0,0062 |
0,00319 |
-0,4737 |
0,2426 |
0,1808 |
0,0948 |
5 |
0,01071 |
0,02014 |
0,00319 |
0,01262 |
0,2426 |
0,9590 |
0,0948 |
0,3289 |
6 |
0,02014 |
0,02957 |
0,01262 |
0,02205 |
0,95908 |
1,6755 |
0,3289 |
0,4525 |
7 |
0,02957 |
0,039 |
0,02205 |
- |
1,67551 |
0 |
0,4525 |
0,5 |
Найдем
теоретические частоты
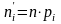 .
Результаты представлены в таблице 2.5:
.
Результаты представлены в таблице 2.5:
Таблица 2.5 – Нахождение теоретических частот
|
|
0,0287 |
1,7794 |
0,0883 |
5,4746 |
0,5638 |
34,9556 |
-0,086 |
-5,332 |
0,2341 |
14,5142 |
0,1236 |
7,6632 |
0,0475 |
2,945 |
Вычислим наблюдаемое значение критерия Пирсона. Для этого составим следующую расчетную таблицу 2.6.
Таблица 2.6 – Вычисление наблюдаемого значения критерия Пирсона
|
|
|
|
|
|
1 |
2 |
1,7794 |
1,9713 |
3,886024 |
2,183896 |
2 |
6 |
5,4746 |
5,9117 |
34,9482 |
6,383699 |
3 |
12 |
34,9556 |
11,4362 |
130,7867 |
3,741508 |
4 |
15 |
-5,332 |
15,086 |
227,5874 |
-42,6833 |
5 |
19 |
14,5142 |
18,7659 |
352,159 |
24,26307 |
6 |
3 |
7,6632 |
2,8764 |
8,273677 |
1,079663 |
7 |
5 |
2,945 |
4,9525 |
24,52726 |
8,32844 |
|
62 |
62 |
|
|
3,296965 |
В таблице приведено значение статистики χ2, равное 3,296965 количество степеней свободы k = 4.
Значение χ2 (критическое) берем из таблицы “Критические точки распределения χ2” для значения степени свободы k = 4 и уровня значимости q = 0,05. X2критич = 9,5.
χ2набл.< χ2критич., т.е. 3,29 < 9,5. Тогда согласно критерию Пирсона имеем нормальное распределение.
Статистическая проверка наличия результатов с грубыми погрешностями.
Определение критерия ν для статистического отбраковывания экстремальных результатов Xextr и сравнение его с критическим значением ν':
ν = ( |Xextr – Xср| / σ) > ν',
Или упрощенная процедура отбраковывания экстремальных отклонений при нормальном распределении погрешностей, например по критерию 3σ в форме |Vextr| > 3σ. В данном случае ν = (Vmax/σx) > ν'. Проверке подвергнем наиболее подозрительные результаты измерений:
|Vmax|
< 3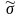 х:
3
х
= 3·
х:
3
х
= 3·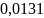 = 0,0393; Vmax
=
0,0314
= 0,0393; Vmax
=
0,0314
Отсюда видно, что результаты с грубыми погрешностями отсутствуют.
Расчет доверительных границ результата измерений Δ и расчет оценки
среднего квадратического отклонения результата измерения.
Оценку
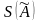 среднего
квадратического отклонения результата
измерения, при ранее рассчитанном
значении S
определяют из формулы:
среднего
квадратического отклонения результата
измерения, при ранее рассчитанном
значении S
определяют из формулы:
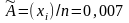
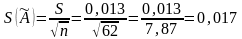
Доверительные границы случайной погрешности ε результата измерения рассчитывают из зависимости:
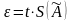
где t – коэффициент Стьюдента, зависящий от доверительной вероятности P и числа результатов наблюдений n.
при
P
= 0,95:

при
P
= 0,99
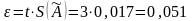
Границы неисключенной систематической погрешности Θ результата измерения вычисляют путем построения композиции всех неисключенных систематических погрешностей. Эти границы (без учета знака) можно вычислить с использованием зависимости:
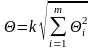 ,
,
где Θi – граница i-й неисключенной систематической погрешности;
k – коэффициент, определяемый принятой доверительной вероятностью.
При Р = 0,95; k = 1,1. Получаем:
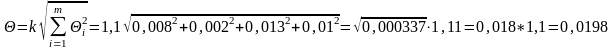
При Р = 0,99; k = 1,4. Получаем:
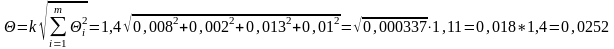
Для оценки значимости неисключенных систематических погрешностей по сравнению со случайными вычислим отношение Θ/ = 0,02/0,017 = 1,176.
Так как отношение неисключенной систематической составляющей погрешности к случайной находится между двумя указанными пределами:
0,8 ≤ Θ/S(Ã) ≤ 8,0,
то границу погрешности результата измерения находим путем построения композиции распределений случайных и неисключенных систематических погрешностей.
Расчет суммарной погрешности.
Коэффициент K - коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей вычисляют по эмпирической формуле:
При Р = 0,95;
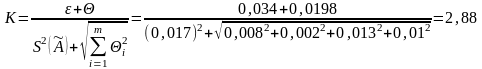
При Р = 0,99;
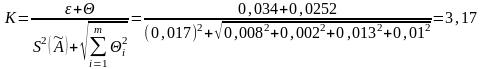
Оценку суммарного среднего квадратического отклонения результата измерения определяют из зависимости
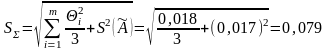
Расчет доверительных границ.
В нашем случае допускается границы погрешности результата измерения Δ (без учета знака) вычисляем с использованием зависимости
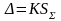 ,
,
При
Р = 0,95

При
Р = 0,99
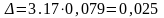
где K – коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей; SΣ – оценка суммарного среднего квадратического отклонения результата измерения.


Рисунок 2.6 – Кривые распределения
Руководствуясь формой записи результатов, предложенной в ГОСТ 8.207 для случая симметричной доверительной погрешности, результат запишем в следующей форме:
(A ± 0,022); P=0,95
(A ± 0,025); P=0,99
Записанный результат означает, что с такой вероятностью (P=0,95 или P=0,99) данный интервал накрывает истинное значение измеряемой величины.