1 .3.4 Расчет нормальных сечений и подбор арматуры в расчетных сечениях второстепенной балки

Рисунок 7 – Расчетные нормальные сечения второстепенной балки;

в пролете (а) и на опоре (б)

Определение площади сечения арматуры при действии положительного момента ведем как для таврового сечения с полкой в сжатой зоне. При действии отрицательного момента полка находится в растянутой зоне, следовательно расчетное сечение будет прямоугольным.

Размеры сечения, принятые по расчету:

мм, мм; мм; =80 мм.

Задаемся величиной с₁ = 30 мм в пролёте и с₂ = 50 мм на опоре.

Тогда рабочая высота сечения:

; .

Предполагая, что нейтральная ось проходит по нижней грани полки, определяем область деформирования для прямоугольного сечения шириной b_eff = 2250 мм и положение нейтральной оси при расчете тавровых сечений:

(1.31)

, следовательно, сечение находится в области деформирования 1в (таблица 6.8).

С помощью таблицы 6.6 находим величину _m, а затем изгибающий момент по формуле:

(1.48) где - коэффициент, учитывающий длительность действия нагрузки, неблагоприятного способа её приложения;

Так как в 1-ом пролете , то нейтральная линия проходит в полке и расчет производится как для элементов прямоугольного сечения с шириной b = b_eff = 2000 мм.

Для бетона класса С¹²/₁₅: ε_cu = 3,5‰; ω_c = 0,810; k₂ = 0,416; C₀ =1,947.

Для арматуры S500: E_s = 2·10⁵ МПа; f_yd = 417 МПа.

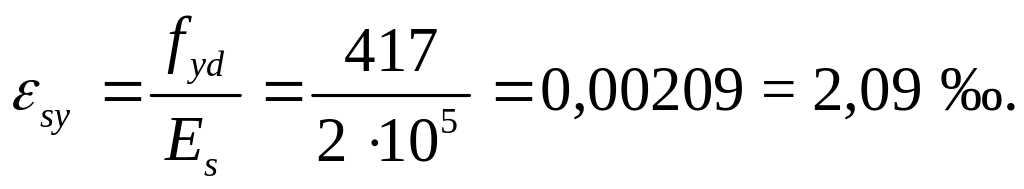(1.33)

(1.34)

(1.35)

В пролете 1 (нижняя арматура) M_sd = 75,17 кНм; d₁ = 0,37 м; b = b_eff = 2250 мм.

Вычисляем значение коэффициента по формуле:

(1.32)

где - коэффициент, учитывающий длительность действия нагрузки, неблагоприятного способа её приложения;

, следовательно, растянутая арматура достигла предельных деформаций.

Находим относительное плечо пары сил:

(1.36)

Требуемая площадь сечения растянутой арматуры:

(1.37)

_{Принимаем 2 стержня Ø16 мм с Ast = 4,02 см}² _{и 1 стержень Ø12 мм с Ast = 1,131 см}²_.

В пролете 2 (нижняя арматура) M_sd = 51,77 кНм; d₁ = 0,37 мм; b = b_eff = 2250 мм.

Вычисляем значение коэффициента :

, следовательно, растянутая арматура достигла предельных деформаций.

Находим относительное плечо пары сил:

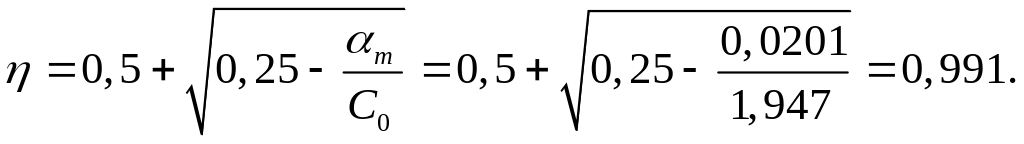
Требуемая площадь сечения растянутой арматуры:

_{Принимаем 2 стержня Ø12 мм с Ast = 2,26 см}² _{и 1 стержень Ø12 мм с Ast = 1,131 см}²_.

_{Минимальная площадь продольной арматуры:}

A_s,min = ρ_min·b_sb·d₁ = 0,0013·200·417 = 0,813 см². (1.49)

В опорных сечениях действуют отрицательные моменты, плита расположена в растянутой зоне, поэтому сечение балки рассматривают как прямоугольное с шириной b = 200 мм = 0,20 м.

Результаты расчета сводим в таблицу 9.

Таблица 9 - Определение площади сечения рабочей арматуры второстепенной балки

Положение сечения	Расположение арматуры	Msd кН·м	am	η	Ast, см2	Ast (прин.), см2	Принятое армирование
1 пролет	нижнее	75,17	0.031	0.9841	4.95	5.15	2Ø16 1Ø12
	Верхняя	-	Монтажная конструкт. арматура			2,26	2Ø12
Опора B	Верхняя	59.06	0.40	0.71	5.71	5.751	3Ø14 1Ø12
2 пролет	Нижняя	51.77	0.02	0.99	3.39	3.39	2Ø12 1Ø12
	Верхняя	6.27	0.04	0.98	0.41	2.26	2Ø12
Опора С	Верхняя	51.77	0.35	0.76	4.65	5.15	2Ø16 1Ø12