2.2.5 Расчет плиты по деформациям

Расчет железобетонных конструкций по деформациямследует производить из условия

a_k ≤ a_lim , (8.33)

где a_k - прогиб (перемещение) железобетонной конструкции от действия внешней нагрузки, мм;

a_lim - предельно допустимый прогиб (перемещение), мм, принимаемый по разделу 10 СНиП 2.01.07.

Для железобетонных элементов прямоугольного, таврового и двутаврового сечений с арматурой, сосредоточенной у верхней и нижней граней, и усилиями, действующими в плоскости симметрии сечения, допускается определять прогиб при изгибе a(∞,t₀) по упрощенной формуле:

(8.34)

где α_k - коэффициент, зависящий от способа приложения нагрузки и схемы опирания элемента;

M_Sd - максимальное значение расчетного момента по предельным состояниям второй группы;

B(∞,t₀) - изгибная жесткость элемента, определяемая при длительном действии нагрузки по формуле:

(8.35)

где E_c,eff - ффективный модуль упругости бетона;

I_II , I - соответственно момент инерции сечения с трещиной и без трещины, определяемый с учетом отношения:

Значения эффективного модуля упругости бетона E_c,eff определяются:

- при действии длительной нагрузки:

где Φ(∞,t₀) - предельное значение коэффициента ползучести для бетона, определяемое в соответствии с указаниями раздела 6.

Значение коэффициента ползучести .

A_sc=0.

(8.36)

(8.37)

(8.38)

(8.39)

(8.40)

Максимальный прогиб в середине пролета свободно опертой однопролетной плиты, загруженной равномерно распределенной нагрузкой:

(8.41)

Вертикальные предельные прогибы плит перекрытия по таб.19 СНиП 2.01.07-85 “Нагрузки и воздействия” составляют при пролете l=3м а_к=1/150, при пролете l=6м а_к=1/200. Для пролета l=5,13 а_к=1/185,5

(8.41)

Максимальной прогиб в середине пролета балки не превышает допустимый, таким образом, проверка выполняется.

2.3 Расчёт и конструирование ригеля

2.3.1 Расчет нагрузок, действующих на ригель

Нагрузка на 1 п.м. ригеля

(2.40)

где - собственный вес ригеля;

,

где – плотность железобетона;

- коэффициент надежности по нагрузке.

Определим расчетный пролет ригеля.

Рисунок 13 – К определению расчетного пролета ригеля

(2.41)

2.3.2 Определение усилий, возникающих в сечениях ригеля от действия внешней нагрузки

Ригель рассматриваем как свободно опёртую балку с максимальным моментом в середине пролёта, опорами для которой служат колонны, а крайними – стены. При расчёте делаем два сечения: по длине ригеля в зоне максимального момента и на опоре в зоне подрезки.

Значение максимального изгибающего момента в сечении ригеля вычислим по формуле:

(2.42)

Значение поперечных сил на промежуточных опорах:

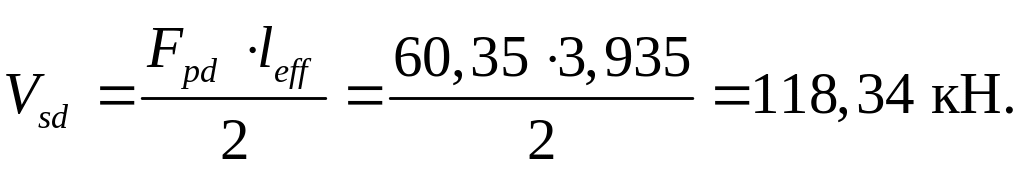(2.43)

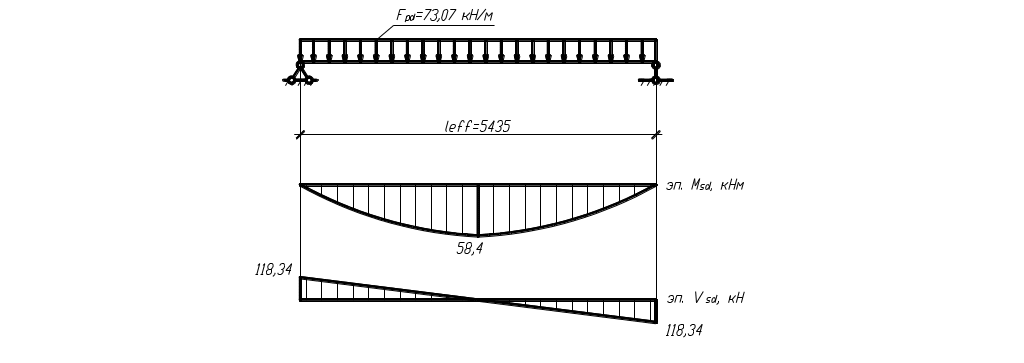
Рисунок 14 – Расчётная схема ригеля