3.6 Расчет прочности наклонных сечений по поперечной силе

Прочность железобетонной балки на действие поперечной силы определяем, в первую очередь, проверкой условия:

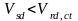(3.11)

Определим значение поперечной силы, воспринимаемой сечением без поперечного армирования:

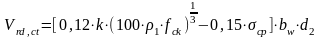,но не менее(3.12)

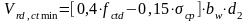
где , принимаем k=1,816

(минимальное значение коэффициента армиро­вания, регламентированное СНБ 5.03.01).

Тогда расчетный коэффициент армирования

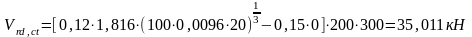
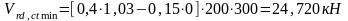
Условие не выполняется, тогда используя метод ферменной аналогии, поперечное армирование определим из услови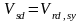й и

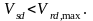
Зададимся углом наклона трещин к горизонтали 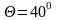и шагом поперечной арматуры S=150мм.

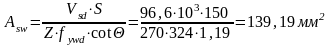
где Z-расстояние между равнодействующими в сечении:

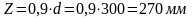
Принимаем два стержня диаметром 10 мм класса S500 (A_sw=157 мм²) c шагом S=150мм.

При этом должны выполняться условия:

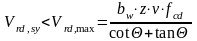(3.13)

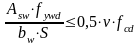(3.14)

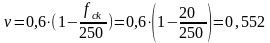
-условие выполняется, прочность по сжатой полосе обеспечена.

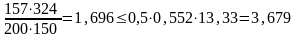-условие выполняется, что означает оптимальность принятого армирования.

На ¼ длины второстепенной балки с обоих её краёв принимаем шаг поперечной арматуры 150 мм, в середине пролёта принимаем шаг 250, т.к. уменьшается значение поперечной силы.

3.7 Построение эпюры материалов

С целью экономичного армирования и обеспечения прочности сечений балки строим эпюру материалов, представляющую собой эпюру изгибающих моментов, которые может воспринять элемент по всей своей длине. Значение изгибающих моментов в каждом сечении при известной площади рабочей арматуры вычисляют по формуле:

M_Rd=f_yd∙A_st∙d∙η,

где d- уточненное значение рабочей высоты сечения;

η- табличный коэффициент, определяемый:

η=1-k₂∙ξ

ξ=(A_st∙f_yd)/(ω_c∙α∙f_cd∙b∙d).

При построении эпюры материалов считают, что обрываемый стержень необходимо завести за точку теоретического обрыва, где он уже не нужен по расчету прочности нормальных сечений, на расстояние анкеровки l_bd. При выполнении обрывов (отгибов) стержней необходимо соблюдать принцип симметрии расположения стержней в поперечном сечении балки. Также следует иметь в виду, что начало каждого отгиба в растянутой зоне располагают на расстоянии точки теоретического обрыва не менее чем 0,5∙d, где d-уточненное значение рабочей высоты сечения. С целью восприятия изгибающего момента от возможного частичного защемления балки на стене в первом пролете арматуру не обрывают, а отгибают на крайнюю опору. Начало отгиба располагают на расстоянии 50-60 мм от внутренней грани стены.

Расчеты, необходимые для построения эпюры материалов выполнены в табличной форме.

Таблица 7-Вычисление ординат эпюры материалов для продольной арматуры

⌀ и количество стержней	Уточненная высота сечения d=hsb-c, мм	Фактическая площадь сечения стержней, Ast, мм2	Расчетное сопротивление арматуры, fyd, МПа	Относительная высота сжатой зоны, ξ	Коэффициент η	Момент MRd, кН∙м
Первый пролет (нижняя арматура b=b’f=162,5cм, с=3,5cм)
2⌀16	31,5	4,02	435	0,032	0,987	54,37
1⌀14	31,5	1,539	435	0,012	0,995	20,98
Первый пролет (верхняя арматура b=bsb=20cм, с=5cм)
2⌀12	30	2,26	435	0,20	0,917	27,05
Опорная арматура. Опора А (b=bsb=20cм, с=5cм)
2⌀12	30	2,26	435	0,20	0,917	27,05
1⌀14	30	1,539	435	0,14	0,914	16,36
Опорная арматура. Опора В (b=bsb=20см, с=5см)
2⌀14	30	3,08	435	0,28	0,884	33,53
1⌀14	30	1,539	435	0,14	0,914	16,36
1⌀12	25	1,131	435	0,12	0,916	10,73
Второй пролет (нижняя арматура b=b’f=162,5см, с=3,5см)
2⌀14	31,5	3,08	435	0,024	0,990	41,78
1⌀12	31,5	1,131	435	0,009	0,996	15,44
Второй пролет (верхняя арматура b=bsb=20см, с=5см)
2⌀12	30	2,26	435	0,20	0,917	27,05
Опорная арматура. Опора С (верхняя арматура b=bsb=20см, с=5см)
2⌀12	30	2,26	435	0,20	0,917	27,05
1⌀12	30	1,141	435	0,10	0,939	13,86

Эпюра материалов должна охватывать эпюру изгибающих моментов.