6.8 Расчет плиты по раскрытию трещин

Значение предельно допустимой ширины раскрытия трещин при практически постоянном сочетании нагрузок (при постоянной и длительной нагрузках):

w_lim = 0,4 мм.

Расчет по раскрытию трещин сводится к проверке условия

w_k≤w_lim,

где w_k– расчетная ширина раскрытия трещин от практически постоянного сочетания нагрузок.

Расчетная ширина раскрытия трещин определяется по формуле:

w_k = β⋅s_rm⋅ε_sm , (6.28)

где s_rm - среднее расстояние между трещинами;

ε_sm - средние относительные деформации арматуры, определяемые при соответствующей комбинации нагрузок;

β - коэффициент, учитывающий отношение расчетной ширины раскрытия трещин к средней, β = 1,3 при расчете ширины раскрытия трещин, образующихся от действия усилий, возникающих при ограничении вынужденных деформаций для сечений, наименьший размер которых (высота, ширина, толщина) составляет 300 мм и менее.

ε_sm = ε_s⋅ψ_s , (6.29)

где ε_s- относительная деформация растянутой арматуры в сечении с трещиной, определяемая в общем случае из решения расчетной системы уравнений деформационной модели от действия изгибающего момента и продольной силы:

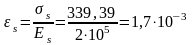(6.30)

где z – плечо внутренней пары сил, в курсовом проекте принимается равным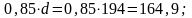

ψ_s - коэффициент, учитывающий неравномерность распределения относительных деформаций растянутой арматуры на участках между трещинами, величину которого следует определять по формуле:

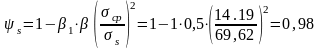(6.31)

β₁- коэффициент, принимаемый для стержневой арматуры периодического профиля 1,0;

β₂- коэффициент, учитывающий длительность действия нагрузки, принимаемый равным при действии длительно действующих и многократно повторяющихся нагрузок 0,5.

Отношение 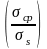допускается принимать при изгибе

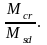
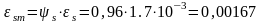
Среднее расстояние s rm между трещинами, мм, нормальными к продольной оси, в изгибаемых и растянутых элементах следует определять по формуле

(6.32)

где ∅ - диаметр стержня, мм, (при использовании в одном сечении стержней разных диаметров допускается принимать в формуле их средний диаметр);

k₁- коэффициент, учитывающий условия сцепления арматуры с бетоном, равныйдля стержней периодического профиля k₁ = 0,8;

k₂- коэффициент, учитывающий вид напряженно-деформированного состояния элемента и принимаемый равнымпри изгибе k₂ = 0,5;

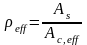(6.33)

где A_s - площадь сечения арматуры, заключенной внутри эффективной площади растянутой зоны сечения A_c,eff ;

A_{c,eff -} эффективная площадь растянутой зоны сечения, определяемая в общем случае как площадь бетона, окружающего растянутую арматуру при высоте, равной 2,5 расстояния от наиболее растянутой грани до центра тяжести арматуры.

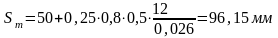
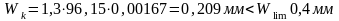
Следовательно, ширина трещин раскрытия не превышает предельно допустимую.

6.9 Расчет плиты по деформациям

Расчет железобетонных конструкций по деформациямследует производить из условия:

a_k ≤ a_lim , (6.34)

где a_k- прогиб (перемещение) железобетонной конструкции от действия внешней нагрузки, мм;

a_lim- предельно допустимый прогиб (перемещение), мм, принимаемый по разделу 10 СНиП 2.01.07.

Для железобетонных элементов прямоугольного, таврового и двутаврового сечений с арматурой, сосредоточенной у верхней и нижней граней, и усилиями, действующими в плоскости симметрии сечения, допускается определять прогиб при изгибе a(∞,t₀) по упрощенной формуле:

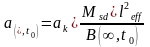(6.35)

где α_k- коэффициент, зависящий от способа приложения нагрузки и схемы опирания элемента;

M_Sd- максимальное значение расчетного момента по предельным состояниям второй группы;

B(∞,t₀) - изгибная жесткостьэлемента, определяемая при длительном действии нагрузки по формуле:

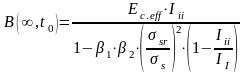(6.36)

где E_c,eff - эффективный модуль упругости бетона;

I_II, I_I - соответственно момент инерции сечения с трещиной и без трещины, определяемый с учетом отношения:

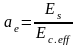
Значения эффективного модуля упругости бетона E_c,eff определяются:

где Φ(∞,t₀) - предельное значение коэффициента ползучести для бетона.