6.5 Расчет прочности сечений, наклонных к продольной оси плиты

Расчет ведем аналогично расчету второстепенной балки.

Прочность железобетонной балки на действие поперечной силы определяем, в первую очередь, проверкой условия:

(6.15)

Определим значение поперечной силы, воспринимаемой сечением без поперечного армирования:

,но не менее (6.16)

где , ,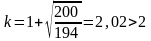 подставляем 2;

0,02 (минимальное значение коэффициента армиро­вания, регламентированное СНБ 5.03.01).

Тогда расчетный коэффициент армирования

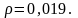
Тогда, с учетом рассчитанных величин получим:

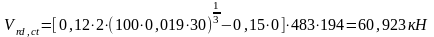
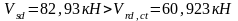
Условие не выполняется, тогда используя метод ферменной аналогии, поперечное армирование определим из условий и

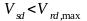
Зададимся углом наклона трещин к горизонтали и шагом поперечной арматуры S=150мм.

где Z-расстояние между равнодействующими в сечении:

Принимаем шесть стержней диаметром 6мм класса S500 (A_sw=170 мм²) c шагом S=150мм.

При этом должны выполняться условия:

(6.17)

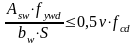(6.18)

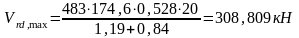
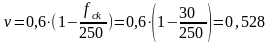
-условие выполняется, прочность по сжатой полосе обеспечена.

-условие выполняется, что означает оптимальность принятого армирования.

6.6Определение геометрических характеристик приведенного сечения

1. Площадь приведенного сечения:

(6.19)

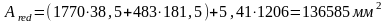
Отношение модулей упругости:

(6.20)

где Е_cm=37·10³МПа– модуль упругости бетона класса С30/37марки П2 по удобоукладываемости;

Е_s=20·10⁴ МПа – модуль упругости для ненапрягаемой арматуры.

2.Статический момент площади приведенного сечения относительно нижней грани:

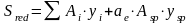(6.21)

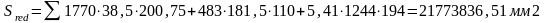
где y-расстояние от нижней грани до центра тяжести i-ой части сечения.

3.Расстояние от нижней грани до центра тяжести приведенного сечения:

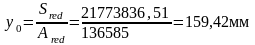(6.22)

4.Момент инерции приведенного сечения относительно оси, проходящей через центр тяжести сечения:

(6.23)

5.Момент сопротивления приведенного сечения относительно нижней его грани:

(6.24)

6. Момент сопротивления приведенного сечения с учетом неупругих деформаций растянутого бетона:

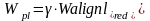(6.25)

где =1,75 для тавровых сечений с полкой в сжатой зоне.

6.7Расчет по образованию трещин

Расчет трещиностойкости сечений, нормальных к продольной оси для изгибаемых элементов следует производить из следующего условия:

М_sd,n≤ M_сr, (6.26)

где М_sd,n – изгибающий момент от нормативной нагрузки,

М_сr – изгибающиймомент, воспринимаемый сечением, нормальным к продольной оси элемента при образовании трещин (усилие трещинообразования).

Усилие трещинообразования допускается определять по упрощенной зависимости как для бетонного сечения по формуле:

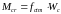, (6.27)

где f_ctm – средняя прочность бетона на осевое растяжение (для бетона класса С30/37f_ctm=2,9 МПа).

W_c – момент сопротивления бетонного сечения.

М_сr=14,19кН∙м>М_sd,к=69,62кН∙м

Условие не соблюдается, следовательно, производим расчет по раскрытию трещин.