
- •Введение
- •Глава I математический аппарат и основные понятия классической электродинамики
- •§ 1.1. Постулаты специальной теории относительности
- •§ 1.2. Четырехмерное пространство и четырехмерная символика
- •§ 1.3. Преобразования Лоренца для координат и времени
- •§ 1.4. Преобразования Лоренца для скоростей и углов
- •§ 1.5. Кинематические «парадоксы» специальной теории относительности
- •§ 1.6. Ковариантная форма преобразований Лоренца
- •§ 1.7. Четырехмерные векторы
- •§ 1.8. Четырехмерные тензоры
- •§ 1.9. Преобразование Лоренца для антисимметричного тензора
- •§ 1.10. Электромагнитные потенциалы и поля
- •§ 1.11. Преобразования Лоренца для напряженности полей и потенциалов
- •§ 1.12. Инварианты электромагнитного поля
- •Глава II релятивистская механика
- •§ 2.1. Четырехмерные векторы импульса и силы
- •§ 2.2. Сила Лоренца
- •§ 2.3. Вариационный принцип Гамильтона в релятивистской механике
- •§ 2.4. Вывод силы Лоренца из уравнений Эйлера-Лагранжа
- •§ 2.5. Релятивистские уравнения Гамильтона
- •Глава III полевая электродинамика
- •§ 3.1. Первая пара уравнений Максвелла в дифференциальной форме
- •§ 3.2. Вариационный принцип Гамильтона в теории поля
- •§ 3.3. Вторая пара уравнений Максвелла в дифференциальной форме для чистого поля
- •§ 3.4. Вторая пара уравнений Максвелла в дифференциальной форме при наличии зарядов и токов
- •§ 3.5. Первая пара уравнений Максвелла в интегральной форме
- •§ 3.6. Вторая пара уравнений Максвелла в интегральной форме
- •§ 3.7. Четырехмерный вектор плотности тока
- •§ 3.8. Четырехмерный вектор плотности силы
- •§ 3.9. Тензор плотности энергии-импульса частиц
- •§ 3.10. Тензор плотности энергии-импульса электромагнитного поля
- •§ 3.11. Вектор Пойнтинга и мощность электромагнитного излучения
- •§ 3.12. Тензор натяжения Максвелла и пондеромоторные силы
- •§ 3.13. Закон сохранения плотности энергии-импульса в дифференциальной форме. Сила Лоренца.
- •Глава IV теория частиц и полей
- •§ 4.1. Об устойчивости статической системы электрических зарядов. Теорема Ирншоу
- •§ 4.2. Собственная масса замкнутой системы заряженных частиц и полей
- •§ 4.3. Происхождение электростатических полей
- •§ 4.4. Системы зарядов в постоянном и неоднородном внешнем электрическом поле
- •§ 4.5. Происхождение магнитно-статистических полей
- •§ 4.6. Система зарядов во внешнем магнитном поле
- •§ 4.7. Применение теории взаимодействия магнитного момента с внешним магнитным полем
- •Глава V электромагнитные волны
- •§ 5.1. Волновое уравнение
- •§ 5.2. Плоские электромагнитные волны
- •§ 5.3. Монохроматическая плоская волна
- •§ 5.4. Неоднородное уравнение Даламбера. Запаздывающие и опережающие потенциалы
- •§ 5.5. Потенциалы и поля произвольно движущегося заряда
§ 1.9. Преобразование Лоренца для антисимметричного тензора
Как мы уже выяснили, любой антисимметричный тензор преобразуется по закону:
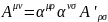 (1.9.1)
(1.9.1)
Вспомним, что
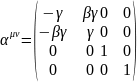 (1.9.2)
(1.9.2)
Распишем одну из компоненту антисимметричного тензора по правилу. Получим
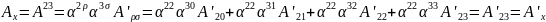
Следовательно,
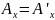 ,
т.е. продольная компонента не преобразуется.
,
т.е. продольная компонента не преобразуется.
Проведя такие же вычисления для остальных компонент антисимметричного тензора, получим
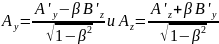 (1.9.3)
(1.9.3)
Таким же образом получены
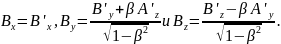 (1.9.4)
(1.9.4)
§ 1.10. Электромагнитные потенциалы и поля
Если в определении произвольного
четырехмерного
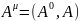 вектора за нулевую компоненту принять
скалярный потенциал φ, а за векторную
компоненту - трехмерный вектор-потенциал,
то мы получим определение четырехмерного
вектора-потенциала
вектора за нулевую компоненту принять
скалярный потенциал φ, а за векторную
компоненту - трехмерный вектор-потенциал,
то мы получим определение четырехмерного
вектора-потенциала
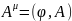 .
С помощью этого вектора можно определить
тензор напряженностей электромагнитного
поля:
.
С помощью этого вектора можно определить
тензор напряженностей электромагнитного
поля:
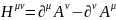 .
(1.10.1)
.
(1.10.1)
Из самого определения этого тензора следует, что он антисимметричен. Антисимметричные тензоры и их основные свойства были достаточно подробно обсуждены выше.
Сейчас
запишем компоненты тензора 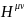
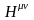 .
Так как тензор антисимметричен, то сразу
можно написать, что
.
Так как тензор антисимметричен, то сразу
можно написать, что
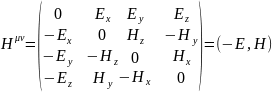 (1.10.2)
(1.10.2)
Здесь E - напряженность электрического поля, а H - напряженность магнитного поля.
Оказывается,
что все компоненты тензора можно вывести напрямую из его определения,
и в результате получим:
можно вывести напрямую из его определения,
и в результате получим:
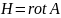 (1.10.3)
(1.10.3)
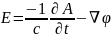 (1.10.4)
(1.10.4)
Мы получили тензор напряженности электромагнитных полей. Иногда в электродинамике используется другой тензор электромагнитного поля, называемый дуальным к основному тензору или дуальным тензором. Дуальный тензор связан с основным следующим соотношением:
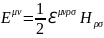 (1.10.5)
(1.10.5)
где - все тот же символ Леви-Чевита.
Исходя из определения, дуальный тензор имеет вид:
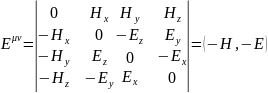 (1.10.6)
(1.10.6)
Проверим некоторые компоненты этого тензора:
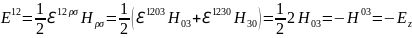 (1.10.7)
(1.10.7)
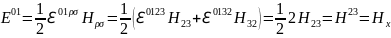 (1.10.8)
(1.10.8)
Можно написать обратное преобразование
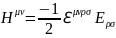 (1.10.9)
(1.10.9)
В общем виде проверка этого соотношения выглядит следующим образом
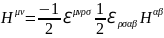
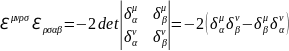
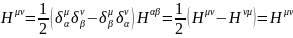 (1.10.10)
(1.10.10)

