§ 1.3. Преобразования Лоренца для координат и времени

Мы пока знаем один четырехмерный вектор 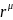. Найдем закон преобразования координат при переходе из одной системы координат к другой. Преобразования Галилея не годятся, т. к. из них вытекает абсолютность времени. Докажем это:

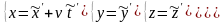(1.3.1)

Будем считать эти преобразования промежуточными (~), и позже они будут заменены на преобразования Лоренца. Подставим это преобразование в выражение для инварианта интервала:

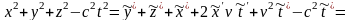
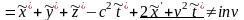(1.3.2)

Таким образом, видно, что инвариантность интервала при таком преобразовании не сохраняется, что противоречит утверждению об инвариантности интервала. Таким образом, у Галилея .

Следовательно, должны существовать другие преобразования. Они были получены Лоренцем. Для вывода мы будем использовать свойства инвариантности интервала. Если считать, что четырехмерный вектор расположен из начала четырехмерных координат, то

(1.3.3)

Преобразуем теперь правую часть выражения (1.3.2) к виду :

Последнее равенство получится, если произвести замену:

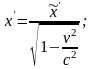
(1.3.4)

Если теперь выразить 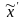и подставить в преобразование Галилея, получим в итоге преобразования

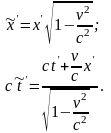(1.3.5)

Согласно преобразованиям Галилея :

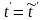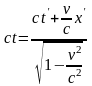. (1.3.6)

Это и есть преобразование Лоренца для времени. Получим теперь преобразование Лоренца для координаты:

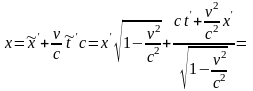
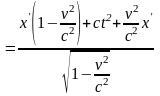(1.3.7)

Окончательно, 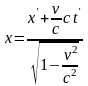. (1.3.8)

В конечном итоге преобразования Лоренца для координат и времени выглядят следующим образом:

; (1.3.9)

Таким образом, мы показали, что будут преобразовываться только время и х-координата, в то время как две другие координаты не преобразуются, т. е. и

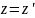
В нерелятивистском приближении преобразования Лоренца переходят в преобразования Галилея, когда v<<c, т. е. <<1.

Иногда нужны обратные преобразования Лоренца (из штрихованной в нештрихованную). Для этого нужно заменить штрихованные величины на нештрихованные и v на –v.

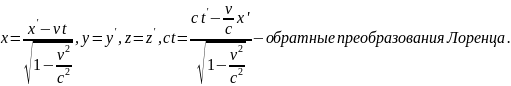
§ 1.4. Преобразования Лоренца для скоростей и углов

После того как были получены преобразования Лоренца для координат и времени, следует определить преобразования Лоренца для скоростей и углов.

Возьмем дифференциалы от преобразований Лоренца для координат и времени:

(1.4.1)

Обозначим u-скорость частицы. По определению

. (1.4.2)

Тогда для проекции скоростей получим:

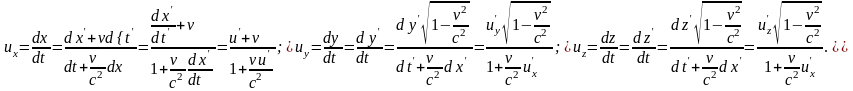(1.4.3)

Эти выражения есть преобразования Лоренца для скоростей. Убедимся теперь, что в нерелятивистском приближении мы получим вновь преобразования Галилея, пренебрегая выражением :

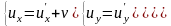(1.4.4)

П

z

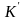ерейдем теперь к преобразованиям Лоренца для углов. Рассмотрим случай больших скоростей. Пусть в системе частица покоится (рис. 1.13). Тогда скорость 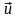в проекциях на ос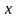и и 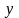можно представить как:

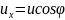
В K′ системе:

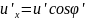
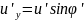
Н

y

айдем :

x

u

φ

Ч

Рис.5

тобы избавиться от функции tgφ, запишем: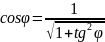

Затем вспомним, что . В конечном итоге получим:

(1.4.5)

Это и будут преобразования Лоренца для углов.